基于参考点的非支配遗传算法-NSGA-III（一）

置顶流浪若相惜

已于 2024-06-03 11:15:07 修改

阅读量3.3w

点赞数 100

分类专栏：算法都很牛的文章标签： NSGA-III 遗传算法多目标进化算法 ENS 参考点

于 2020-12-21 21:13:56 首次发布

本文链接：https://blog.csdn.net/ztzi321/article/details/111304393

版权

算法都很牛的专栏收录该内容

16 篇文章

订阅专栏

序：漫漫长路，不知归期，但至少还是把小计划实现了！尽管小计划开展一路坎坷，中途也差点放弃，但是最终还是咬牙坚持，并实现了NSGA-III算法。说实话，NSGA-III算法相较NSGA-II难度增加了数倍，理解起来也相对困难，且参考的资料及代码相对较少，建议现阶段非计算机人士在无别人指引的情况下, 短期放弃此算法的研究（😂😂），“敢问路在何方？路在脚下…”。然后再定接下来的小计划，约束条件下的NSGA-III算法以及串联迭代多目标算法的代码复现，实现”伪双层交互“思想的迭代方法（😔这个实现起来🚹）。

服了！写完后全部消失了！我能怎么说？我还保存了，客服说有保存记录但没法回滚，我想问这技术有啥用呢?继续。。。

文章目录

废话不多说了，直接上干货。按照常规操作，先上参考的博客、论文及代码。

参考资料

参考博客

遗传算法之NSGA-III原理分析和代码解读
NSGA3算法及其MATLAB版本实现
NSGA3理解（NSGA3算法及其MATLAB版本实现）
多目标优化算法（四）NSGA3(NSGAIII)论文复现以及matlab和python的代码 (该博客与2基本上一致，应该是一个作者所写，1在解读均一化的时候估计也参考了此作者的思路)
余弦距离介绍
platEMO
一起来学演化计算-SBX(Simulated binary crossover)模拟二进制交叉算子详解

参考论文

因参考论文较多，此直接给予所有论文，请点击下载。论文中重要的部分已做了注解和标注。

Y. Tian, R. Cheng, X.Y. Zhang, and Y.C. Jin, “PlatEMO: A MATLAB platform for evolutionary multi‐objective optimization [educational forum],” IEEE Computational Intelligence Magazine, 2017, 12(4): 73‐87.
2.K. Deb, H. Jain . An Evolutionary Many-Objective Optimization Algorithm Using Reference Point-Based Nondominated Sorting Approach, Part I: Solving Problems With Box Constraints[J]. IEEE Transactions on Evolutionary Computation, 2014, 18(4):577-601.
Y. Tian , X. Xiang , X. Zhang , et al. Sampling Reference Points on the Pareto Fronts of Benchmark Multi-Objective Optimization Problems[C]// 2018 IEEE Congress on Evolutionary Computation (CEC). IEEE, 2018.
X. Zhang, Y. Tian, R. Cheng, and Y. Jin, “An efficient approach to nondominated sorting for evolutionary multiobjective optimization,” IEEE Trans. Evol. Comput., vol. 19, no. 2, pp. 201–213, Apr. 2015.
I. Das and J. Dennis, “Normal-boundary intersection: A new method
for generating the Pareto surface in nonlinear multicriteria optimization
problems,” SIAM J. Optimization, vol. 8, no. 3, pp. 631–657, 1998.
K. Deb, R.B. Agrawal, Simulated binary crossover for continuous search space, Complex Systems. 9 (1995) 115–148.

参考代码

注：这里我们仅介绍matlab版本，需要说明的是，K. Deb大神团队并没有给予NSGA-III算法实现的代码，因此，现NSGA-III版本存在较少且不符原文版本，请慎重选择！

主要参考的代码：platEMO以及MOEA-dev两个版本。

EMO现存共性问题及NSGA-III提出

NSGA-II算法面临着EMO共性的问题：

在随机选择的目标向量集合中，非支配解的比例随着目标数量的增加而呈指数级增大。
在实现种群多样性的时候，采用如NSGA-II拥挤度或者聚类算子等方法存在着较大的计算开销和更高的存储开销（时间和空间复杂度），如在NSGA-II中存储空间增加了 $O(N^2)$
难以实现多维度前沿的可视化
重组操作的效率
权衡面的表示以及决策者的选择
高维难以收敛及前沿解集均匀分布问题

前两个问题中的非支配解数量以及种群的多样性问题，可以通过设置大ε-dominated的方法来实现。第四个问题，可以使用交配限制方案或强调近亲本解决方案的特殊重组方案来解决（如SBX交叉方法）。而第三和第五个问题相对来说实现难度比较大。有些代码给予了多个目标函数下Pareto解集的可视化，我个人认为这种展示方式不乏是一种有效方式，但是这种表示方式不能体现多目标之间的权衡关系。如下图所示 (4个目标函数)。

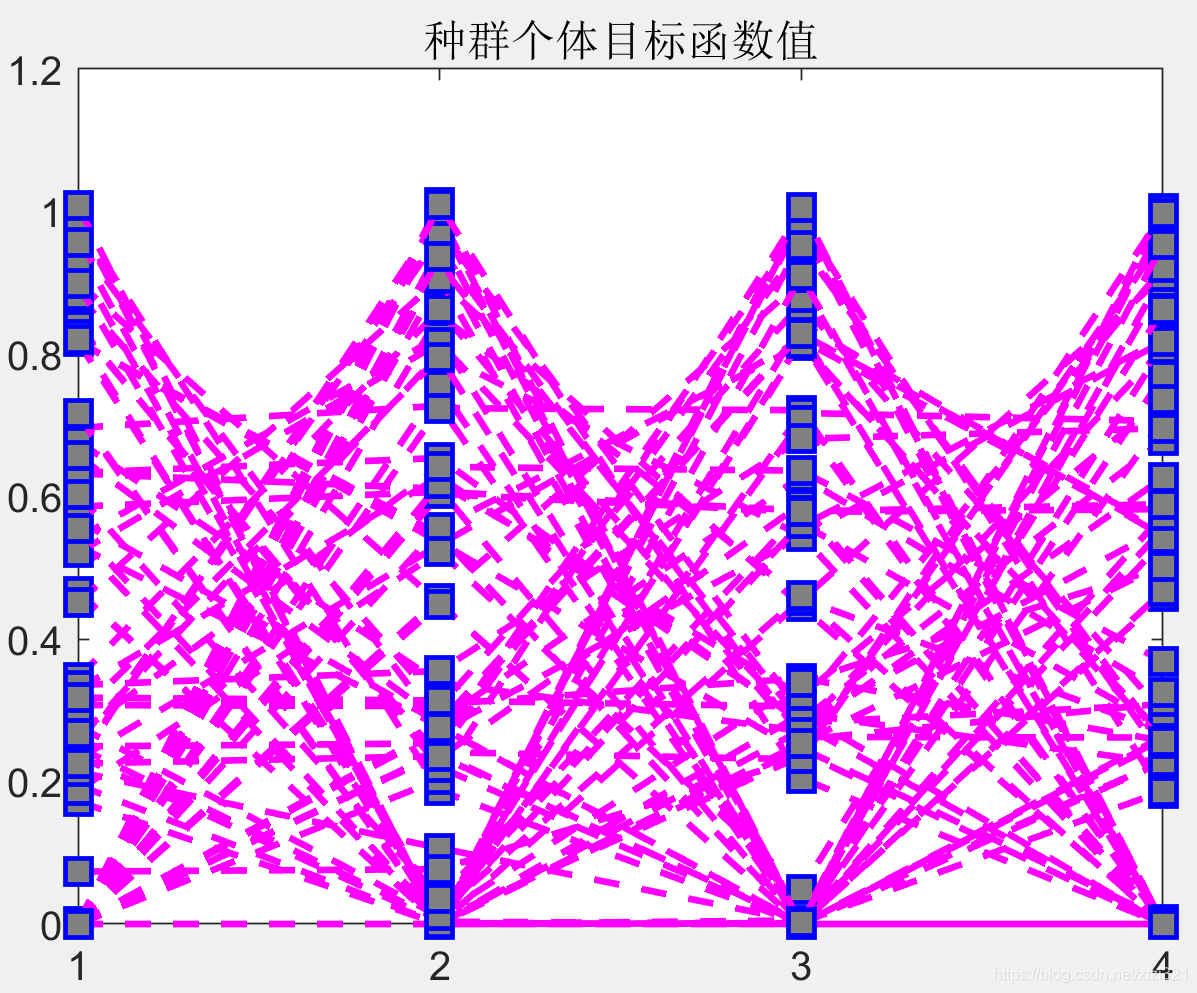
针对第六个问题，已经有研究从提供预设搜索方向和参考点两个方面展开，NSGA-III算法也是从提供预设的参考点的方式，用于解决高维目标以及前沿解集均匀分布问题，避免所获得解集局部最优。

何为参考点？

既然NSGA-III算法是给予预设参考点的方式来处理上述问题的，那么什么是参考点，它又用来做什么呢？

其实这个问题当前我无法很好的回答，问题的答案应该在Das and Dennis那篇文章里，那么，它用来做什么呢？按照NSGA-III文章内容中所述，参考点的目的就是为了获取种群个体与响应参考点之间的映射关系（即垂直距离），进而使得种群超更接近参考点的方向进化，进而事参考点的分布更加均匀。

NSGA-III算法介绍

接下来，步入我们最为核心的部分，NSGA-III算法的介绍。首先，我们需要对比说明一下NSGA-III算法与NSGA-II算法之间的不同。实际上，NSGA-III算法仅在选择Pareto解集的时候采用了基于参考点的方式，而NSGA-II则采用了拥挤度距离的方式来进行筛选（进化理论中也叫环境选择），且拥挤度距离的方式已经不能很好的处理多个目标的问题。

NSGA-III总体实现过程

NSGA-III实现过程，我这里不再单独做图介绍，具体的步骤我们采用论文中的伪代码，然后我对伪代码所要进行的操作转换为比较直白的语言讲解，伪代码如下：

Input: $Z^s，Z^a ,P_t$ ，即有 $Z^s$ 个参考点或者提供的期望点 $Z^a$ （这里我称之为“偏好”）以及父代 $P_t$ ;
Output: 新的一代或者子代（进化后的） $P_{t+1}$ ;

创建归档存储集合 $S_t$ , $i = 1$ 表示等级；
交叉与变异产生新的群体 $Q_t$ ；
获取父代与子代集合（即Niching) $R_t$ ;
非支配等级划分 $F_1,F_2,...）$
（5-7）不断将等级划分后的个体，按照等级的高低排序，将低等级（Rank小的）的等级集合依次存入 $S_t$ 中，直到 $S_t$ 的个数 $S_t|$ 大于等于种群个数 $N$ ;
(8-10) 最后一个前沿假设为 $F_l$ , 若 $S_t|=N$ , 则下一迭代初始种群 $P_{t+1}=S_t$ ; 否则进行基于参考点的选择操作；
（11-13）令 $P_{t+1}=\bigcup_{j=1}^{l-1}F_j$ （注：截至到l-1前沿）,那么 $F_l=N-|P_{t+1}$ ，即l层前沿的个数；
（14）标准化目标函数并创建参考集（详见标准化及参考点创建过程）；
（15）创建种群个体与参考点之间的 “映射关系”，其中 $\pi(s)$ 是距离种群个体最近的参考点， $d(\bf s)$ 是参考点与种群个体之间的距离；
计算小生境参考点的出现次数（这个小生境是针对前l-1前沿的，即 ${\bf s} \in S_t / F_l$ ）；
选择小生境中被选择较少的参考点，并从 $F_l$ 前沿中寻找 $K$ 个种群个体（详见：最后前沿种群个体选择）

注：以下 $S_t$ 均是 $\geq N$

参考点创建

接下来，让我开始正是的了解NSGA-III算法的整个过程。首先，我们说了NSGA-III是基于参考点的进化算法，因此，我们首先应该知道参考点是如何进行创建的。关于参考点的创建我们这里仅给出创建过程，不给予证明过程，具体详见Das and Denni’s文章。

关于创建方法，Y. Tian 大神在《Sampling Reference Points on the Pareto Fronts of
Multi-Objective Optimization Problems》一文中给予了具体的操作步骤，如下：

定义一个 $M$ 维unit simplex（中文不清楚怎么翻译）的参考点集合 ${\bf s}=(s_1,s_2,...,s_M)$ , 则任一参考点坐标值 $s_j \in \begin {Bmatrix} \frac {0} {H},\frac {1} {H},...,\frac {H} {H}\end {Bmatrix},\sum_{j=1}^M s_j=1 \tag 1$ 其中， $H$ 是每个目标上的divisions（分段个数）；
那么怎么求得参考点的坐标值呢？文章中给出了求解步骤如下

如何理解呢？我们举一个H=5,M=3的例子，解释一下从x-s的创建过程,图解参考下图。
首先，构建 $M - 1$ 维 $\bf x$ 的组合，其中 $\in \begin{Bmatrix}\frac{0}{H}, \frac{1}{H},...,\frac{H+M-2}{H},\end {Bmatrix}$ ;
然后，对于 $x\in \bf x$ 进行如下操作并获得新的 $x_{ij}=x_{ij}-\frac{j-1}{H}$ ;
最后获取每一个目标函数上的坐标值：
$\begin{cases} s_{ij}=x_{ij}-0,\ j=1\\ s_{ij}=x_{ij}-x_{i(j-1)},\ 1<j<M \\s_{ij}=1-x_{i(j-1)}, \ j=M\end{cases} \tag 2$
这样的话，我们最终将获取： $refCount=\begin {pmatrix} H+M-1\\ H\end {pmatrix}=C_{H+M-1}^H=C_{H+M-1}^{M-1} \tag 3$
举例说明，若H=4，M=3，则共产生15个参考点，如下图所示：

但与此同时，我们可以发现这样创建参考点的方法会出现一个问题。即当 $H < M$ 时，将仅会产生“边界参考点”，即使在 $H = M$ 的时候，仅会产生一个“中间参考点”，如下图所示：

为了解决这个问题，Deb and Jain’s给出了边界与中间参考点（boundary and intermediate reference points）共同构建参考点的方法。其具体操作方法同上述过程，不同点在于中间参考点的坐标值 $s_{ij}^,=\frac{1}{2} s_{ij}+\frac{1}{2M}$ , 具体计算过程如下所示：

注意：1. 中间参考点的计算坐标过程是独立的;2. 参考点总个数为 $S=S_1\bigcup S_2$ ;3 .建议当 $\leq 5$ 时，用Das and Denni‘s方法，其它情况用Deb and Jain’s方法

代码实现

function [W,N] = UniformPoint(N,M)
%UniformPoint - Generate a set of uniformly distributed points on the unit
%hyperplane.
%
%   [W,N] = UniformPoint(N,M) returns approximately N uniformly distributed
%   points with M objectives on the unit hyperplane.
%
%   Due to the requirement of uniform distribution, the number of points
%   cannot be arbitrary, and the number of points in W may be slightly
%   smaller than the predefined size N.
%
%   Example:
%       [W,N] = UniformPoint(275,10)
    H1 = 1;
    while nchoosek(H1+M-1,M-1) <= N
        H1 = H1 + 1;
    end
    H1=H1 - 1;
    W = nchoosek(1:H1+M-1,M-1) - repmat(0:M-2,nchoosek(H1+M-1,M-1),1) - 1;%nchoosek(v,M),v是一个向量，返回一个矩阵，该矩阵的行由每次从v中的M个元素取出k个取值的所有可能组合构成。比如：v=[1,2,3],n=2,输出[1,2;1,3;2,3]
    W = ([W,zeros(size(W,1),1)+H1]-[zeros(size(W,1),1),W])/H1;
    if H1 < M
        H2 = 0;
        while nchoosek(H1+M-1,M-1)+nchoosek(H2+M-1,M-1) <= N
            H2 = H2 + 1;
        end
        H2 = H2 - 1;
        if H2 > 0
            W2 = nchoosek(1:H2+M-1,M-1) - repmat(0:M-2,nchoosek(H2+M-1,M-1),1) - 1;
            W2 = ([W2,zeros(size(W2,1),1)+H2]-[zeros(size(W2,1),1),W2])/H2;
            W  = [W;W2/2+1/(2*M)];
        end
    end
    W = max(W,1e-6);
    N = size(W,1);
end

交叉与变异

这里我们仅说明一下交叉变异的方法，并给予交叉变异方法的介绍资料。Deb 大神在文章说，建议交叉操作时采用模拟二进制交叉算法（SBX）,变异采用多项式变异方法（Ploynomial mutation）。详细介绍请参考：SBX方法； Ploynomial mutation

代码实现

     %% Genetic operators for real encoding
            % Simulated binary crossover 模拟二进制交叉方法
            beta = zeros(N,D);
            mu   = rand(N,D);
            beta(mu<=0.5) = (2*mu(mu<=0.5)).^(1/(disC+1));
            beta(mu>0.5)  = (2-2*mu(mu>0.5)).^(-1/(disC+1));
            beta = beta.*(-1).^randi([0,1],N,D);
            beta(rand(N,D)<0.5) = 1;
            beta(repmat(rand(N,1)>proC,1,D)) = 1;
            Offspring = [(Parent1+Parent2)/2+beta.*(Parent1-Parent2)/2
                         (Parent1+Parent2)/2-beta.*(Parent1-Parent2)/2];
            % Polynomial mutation 多项式变异方法
            Lower = repmat(lower,2*N,1);
            Upper = repmat(upper,2*N,1);
            Site  = rand(2*N,D) < proM/D;
            mu    = rand(2*N,D);
            temp  = Site & mu<=0.5;
            Offspring       = min(max(Offspring,Lower),Upper);
            Offspring(temp) = Offspring(temp)+(Upper(temp)-Lower(temp)).*((2.*mu(temp)+(1-2.*mu(temp)).*...
                              (1-(Offspring(temp)-Lower(temp))./(Upper(temp)-Lower(temp))).^(disM+1)).^(1/(disM+1))-1);
            temp = Site & mu>0.5;
            Offspring(temp) = Offspring(temp)+(Upper(temp)-Lower(temp)).*(1-(2.*(1-mu(temp))+2.*(mu(temp)-0.5).*...
                              (1-(Upper(temp)-Offspring(temp))./(Upper(temp)-Lower(temp))).^(disM+1)).^(1/(disM+1)));

高效的非支配排序方法（ENS）

在进行选择之前，需要对种群个体进行非支配排序，在NSGA-II中我们介绍过算法采用的非支配排序是两两对比，且同时对比了每一个目标函数值，然后一级一级的获取种群个体的等级，但这样的非支配排序需要消耗更多计算时间 $O(MN^2)$ 与存储空间 $O(N^2)$ 。为了减少时间和空间复杂度，本博客采用了Zhang X.Y. and Y. Tian团队提供的一种高效非支配排序方法—ENS。那么这种方法与之前的非支配方法有什么不同呢？在论文中作者提到ENS方法仅需对比前边已经分配前沿的种群个体，避免不必要的对比。

啥意思呢？接下来我们用图来说明两者的排序不同，可能就会豁然开朗了。

NSGA-II非支配排序方式

ENS非支配排序方式

接下来我们就详细的介绍一下ENS非支配排序方法，该方法主要包括以下几步：

给种群按照第一目标函数值进行排序, 若第一目标函数相同，则按照第二目标函数对比，依次类推；若所有目标函数值均相等，则任意排列；
创建顺序搜索策略对每个种群个体进行排序，等级划分

需要强调一点：对于执行完第一步之后，种群个体存在这样一种内在的关系：若 $m < n$ ，则必然不会存在 $p_n \prec p_m$ 的情况，因为 $p_m$ 中至少存在第一个目标函数小于 $p_n$

如何顺序搜索策略呢？我们首先将伪代码附上，然后一一解释。

Input: 已排序的 $P [n]$ ,以及前沿集合 $\bf F$ ，初始设置 $\bf F=\bf inf$ ;
Output: 返回种群个体的前沿等级；

(1-2) 令 $x = s i ze (F)$ 表示已经被赋予前沿等级的个数, 当前搜索前沿等级 $k$ ;
当 $\le N$ 时进行如下操作（保证种群个数，但一般 $x\ge N$ ）:
从种群中按顺序依次选择个体 $p[1]\sim p[N]$ ，然后与其前边已经分配前沿的个体进行对比，若当前前沿中不存在支配所对比的个体 $p [n]$ 时，则 $R ank (p [n]) = k$ , 否则的话不给予前沿分配，即 $R ank (p [n]) = in f$ ；前后种群之间的关系可以通过下图来表示，原文中也给予了理解。

注：当完成一轮前沿分配后，后边的种群个体仅需与当前前沿相同的种群个体进行比较，然后看其支配关系即可，因为小于当前前沿的时候已经说明了后边的种群个体一定被前边种群支配

举个例子：如下图所示，在第1前沿分配完成后，第6个种群个体前沿=inf，也就说前边一定存在支配种群个体6的个体存在，我们查看一下目标函数发现是第5个种群个体支配第6种群个体（当然第4个也支配），但只要有支配的就可以了。
在这里插入图片描述
当进行第2个前沿分配时，我们仅需给 $R ank (p [n]) = in f$ 对比分析并分配前沿，我们从前边已经知道，第6个种群 $R ank = in f$ ,且前5个种群个体 $\neq2$ , 同时，第5个个体支配它，因此分配给了第6个体为当前前沿，即第2前沿；而第8个个体仅需与第6个前沿对比，但第6个个体的目标函数3大于第8个种群，因此，第8个种群不被6支配，即存在于前沿2中，继续分配 $R ank (p [8]) = 2$ 。
在这里插入图片描述
代码实现

function [FrontNo,MaxFNo] = ENS_SS(PopObj,nSort)
    [PopObj,~,Loc] = unique(PopObj,'rows');% Unique values in array and ranked with ascending order;  return new array, row index, and array index based on return array index to construct original array 
    % A = [9 2 9 5];Find the unique values of A and the index vectors ia and ic, such that C = A(ia) and A = C(ic).
    % C = [2     5     9];ia = [2 4 1]';ic=[3 1 3 2]'
    % 已经按照第一列排序
    Table          = hist(Loc,1:max(Loc));% Histogram plot  not recommanded use histogram x轴表示分类中位数，y表示个数
    [N,M]          = size(PopObj);
    [PopObj,rank]  = sortrows(PopObj);% 默认第一列也就是first objective
%     if ~(all(PopObj(:) == PopObj1(:)))
%         disp(2)
%     end
    FrontNo        = inf(1,N);
    MaxFNo         = 0;
    while sum(Table(FrontNo<inf)) < min(nSort,length(Loc))%what means? 意思就是说我获取的Pareto Front数量要不应超过种群个数
        MaxFNo = MaxFNo + 1;%走过一次for 1:N后所有非支配的解将给与FrontRank，剩余的inf则是被支配的解，需要对其进行赋予FrontRank
        for i = 1 : N
            if FrontNo(i) == inf
                Dominated = false;
                for j = i-1 : -1 : 1
                     if FrontNo(j) == MaxFNo
                        m = 2;
                        while m <= M && PopObj(i,m) >= PopObj(j,m)
                            m = m + 1;
                        end
                        Dominated = m > M;
                        if Dominated || M == 2
                            break;
                        end
                    end
                end
                if ~Dominated
                    FrontNo(i) = MaxFNo;
                end
            end
        end
    end
    FrontNo(rank) = FrontNo;
    FrontNo = FrontNo(:,Loc);%这一步就是借用的unique函数的C(ic)获得原矩阵A也即是PopObj，然后返回Popobj的FrontRank
end

最后一前沿个体选择

同NSGA-II算法一样，在选择部分首先可以根据支配等级来选择等级高的。但是，我们往往在分配完等级后获得的种群个体数会≥N，也就说关键在最后一个前沿中如何选择个体。在NSGA-II算法中，我们采用的是基于拥挤度距离的方式来筛选（原理如下图，详细请参考：多目标非支配排序遗传算法-NSGA-II（一)），而在NSGA-III中则采用基于参考点的方式来截取最后一个前沿中的个体。在选择过程中主要包括：自适应的种群标准化、种群个体与参考点“映射关系”、小生境保护操作。

自适应的标准化

对于标准化，我相信大家都很清楚了，标准化的目的就是为了能使不同量纲或者范围的量进行对比。对于多个目标函数的选择操作来讲，需要进行除量纲，确定哪个个体留下，哪一个被剔除。前边我们讲了，构建参考点的是建立在超平面上的。我们选择参考点的目的就是为了构建参考点与种群个体之间的映射，然后选择接近参考点的种群个体，然后选择。那么这个超平面必然会在每个目标坐标系上有个交点，那我们通过种群个体各目标函数值除以各目标坐标系截距不就实现了去量纲化嘛。但是截距也好，目标函数值也好，都是应该有响应的参照对象的，也就说需要确定原点。我们假设原点（“理想点”）为我们各个目标函数的理想值 $\overline z_{min}=\lbrace z_1^{min},z_2^{min}, ...., z_M^{min}\rbrace$ ，那种群的标准化就可以表示为：
$f_i^n=\frac{f_i^,}{a^,}=\frac{f_i-z_i^{min}}{a-z_i^{min}}， i=1,2,...M, \sum_{i=1}^Mf_i^n=1 \tag 4$ 那我们的问题转化为如何求各个目标上的截距。

那这个截距如何求呢？论文引用了极端点（extreme point）来求解截距（如下图 $z^{i,max}$ ），啥是极端点呢？在多个目标函数中，极端点就是那个仅在一个目标函数方向比较大，而在其它目标方向比较小的点。

这里我引用他人博文中的解释:
我们还是举三个目标的问题作为例子，我们初始化种群后，会得到很多个体，他们的目标值可能是（1，3，0.3），（2，6，0.3），（0.1，0.2，3）等等，如果有一些点如果在一个目标上的值很大，在另外两个目标上的值很小，这些点就更靠近这个坐标轴，这个就是所谓的 extreme points，目标就是找到在一个方向上值很大，另外两个目标值很小的点，三个目标的问题话对应我们可以找到三个这样的 extreme points。
论文中将这个极值点表示为ASF方程中，固定第一个坐标轴，（1，0.2，0.3）/（1，10e-6, 10e-6），这个时候最大的肯定是0.3这个方向，在固定第一个坐标轴时。
$ASF(x,{\bf w})=max_{i=1}^M f_i^n/w_i \tag 5$
在所有种群中我们仅需要找到最小的那个就可以确定每个目标方向的极端值。比如（1，0.6，0.3）在ASF后变为0.610e6，（1，0.2，0.3）在ASF后变为0.310e6，（1，0.1，0.2）在ASF后变为0.210e6，这三个点那个作为extreme points最为合适，我想现在你肯定知道了，0.210e6是最小的，对应（1，0.1，0.2）是最合适的。这就是原文Thereafter, the extreme point in each objective axis is identified by finding the solution (x ∈ St) that makes the following achievement scalarizing function minimum with weight vector w being the axis direction这句话的意思，也是NSGA3算法最难理解的一步。
$z_j^{max}=minASF(x,{\bf w})=minmax_{i=1}^M f_{ij}^n/w_i, j=1,2,...,N \tag 6$

然后根据超平面与截距之间的关系，请参考台湾师范大学教授那个C版本的NSGA3的详细说明理解，即可获得 $z_j^{max}$ 与 $a_j$ 之间的关系。

// Given a NxN matrix A and a Nx1 vector b, generate a Nx1 vector x
// such that Ax = b.
//
// Use this to get a hyperplane for a given set of points.
// Example.
// Given three points (-1, 1, 2), (2, 0, -3), and (5, 1, -2).（这里就是我们的extreme point）
// The equation of the hyperplane is ax+by+cz=d, or a'x +b'y + c'z = 1.
// So we have
//
//    (-1)a' + b' + 2c' = 1.
//    2a' - 3c' = 1.
//    5a' + b' -2c' = 1.
//
// Let A be { {-1, 1, 2}, {2, 0, -3}, {5, 1, -2} } and b be {1, 1, 1}.
// This function will generate x as {-0.4, 1.8, -0.6},
// which means the equation is (-0.4)x + 1.8y - 0.6z = 1, or 2x-9y+3z+5=0.
//
// The intercepts are {1/-0.4, 0, 0}, {0, 1/1.8, 0}, and {0, 0, 1/-0.6}.

这里我们附上伪代码来说明整个过程。

代码实现

    Extreme = zeros(1,M);
    w       = zeros(M)+1e-6+eye(M);
    for i = 1 : M
        [~,Extreme(i)] = min(max(PopObj./repmat(w(i,:),N,1),[],2));% Extreme(i)表示种群索引;max各个目标最大，然后获取各个种群中最小的那个
    end
    % Calculate the intercepts of the hyperplane constructed by the extreme
    % points and the axes；Algorithm 2 第6-7步
    Hyperplane = PopObj(Extreme,:)\ones(M,1);%A的逆矩阵是 A1，则 B/A = B*A1，A\B = A1*B ,且Hyperplane是列向量
    a = 1./Hyperplane;%获取每个方向的截距,其实这个截距也是减去理想点之后的，这里我称之为“理想截距”
    if any(isnan(a))%若a的元素为NaN（非数值），在对应位置上返回逻辑1（真），否则返回逻辑0（假）
        a = max(PopObj,[],1)';
    end
    % Normalization Algorithm 2第
    %a = a-Zmin';
    PopObj = PopObj./repmat(a',N,1);%如果a、b是矩阵，a./b就是a、b中对应的每个元素相除，得到一个新的矩阵；

种群个体与参考点“映射关系”

我这里将其称之为种群个体与参考点的“映射关系”，啥意思呢？我们前边已经创建了“理想”的超平面，然后在超平面上创建了参考点。这个超平面的参考点具有均匀的分布，因此，我们需要种群朝着Pareto前沿面的方向不断的进化，这个过程就需要我们构建种群个体与参考点之间的“映射关系”。

那么如何构建一种“映射关系”使得种群朝着Pareto面进化呢？更确切地说如何构建种群个体与参考点之间的关系，使之种群更接近参考点呢？我们很自然的就想到距离，也就是构建参考点与种群个体的距离，然后距离靠近参考就可以认为这个种群个体被选择。

好了，接下来我们就开始构建这种“映射关系”（距离关系）。前边，我们说了，为了目标之间的公平，我们对种群坐标也好，截距也好都进行了标准化，而这个标准化的起点，也就是我们设置的“理想点”或者原点 $z_i^{min}$ 。然后，我们连接参考点与原点，构建一条条射线，种群个体到射线的距离作为两者之间的距离关系，距离越小，种群越能被选中，示意图如下：

思路我们讲完了，接下来还是附上伪代码，我一步步的通俗化讲解。

Input: 参考点与种群集合 $Z_r, S_t$ (前边我们已经说明了 $S_t \ge N$ );
Output: 距离每个种群个体最小的参考点 $\pi ({\bf s} \in S_t)$ ，种群个体与最近参考点的距离 $d({\bf s}\in S_t)$ ;

首先构建每个参考点的与原点之间的“射线”—参考线 $\bf w$ ;
对于每一个种群个体，我们都将其与每一个参考点进行映射关系的构建，求得每个种群个体与每一个参考点射线之间的距离 $d^{\bot}({\bf s},\bf w))$ ，这个距离可以是欧氏距离、余弦距离等，本博客采用的是余弦距离（详情请看：余弦距离介绍）。
获取每个种群个体距离最小的参考点 $\pi({\bf s})={\bf w}:argmin_{{\bf w} \in Z_r}d^\bot(\bf s,w)$
计算每个种群个体与参考点间最小距离 $d^{\bot}({\bf s},\pi({\bf s}))$

代码实现

  %% Associate each solution with one reference point
    % Calculate the distance of each solution to each reference vector
    Cosine   = 1 - pdist2(PopObj,Z,'cosine');%cosine’ 针对向量,夹角余弦距离Cosine distance(‘cosine’)余弦相似度= 1-余弦距离 衡量两个个体之间的差异
    %pdist2 pairwise distance between two sets of observations
    %杰卡德距离Jaccard distance(‘jaccard’)Jaccard距离常用来处理仅包含非对称的二元(0-1)属性的对象。很显然，Jaccard距离不关心0-0匹配[1]。
    %夹角余弦距离Cosine distance(‘cosine’)与Jaccard距离相比，Cosine距离不仅忽略0-0匹配，而且能够处理非二元向量，即考虑到变量值的大小。
    %对这两者，距离与相似度和为一。
    %https://www.cnblogs.com/chaosimple/archive/2013/06/28/3160839.html

    Distance = repmat(sqrt(sum(PopObj.^2,2)),1,NZ).*sqrt(1-Cosine.^2);% Popobj距离*sinα，需要注意，每个参考点（种群）均与每一个种群个体（参考点）构成一个夹角，即两两关系
    %Distance = pdist2(PopObj,Z,'euclidean');%上面注释的两个语句也可以哦
    % Associate each solution with its nearest reference point
    [d,pi] = min(Distance',[],1);%距离最小，则参考点经过的line将与种群个体具有最小的距离，也就是说参考点接近种群个体，每一列是一个种群个体

小生境保留操作

上边我们构建了种群个体与参考点之间映射关系，获取了每个种群个体距离最小的参考点以及它们之间的距离。前边都是热身工作，接下来，我们正式对最后一前沿种群个体进行操作，筛选最后一前沿种群个体。

同NSGA-II非支配一样，我们已经获取了前 $l - 1$ 前沿个体，无论它属于哪一个前沿，我们需要选择它们所有的个体。对于最后一前沿种群个体在选择时，同拥挤度距离选择一样，要充分考虑种群的多样性。如何保存呢?我们知道拥挤度距离是在考虑种群非支配等级后，距离大的作为选择的依据，进而实现种群的多样性，避免种群收敛过快，出现局部收敛的情况。同理，在NSGA-III中，我们同样在考虑前 $l - 1$ 前沿等级的情况下，根据参考点被选择的个数，选择参考点被选择较少的作为最后一前沿种群个体选择的依据，进而实现选择。还是老样子，我们讲解完大体思路，附上伪代码，然后一一解释。

Input: 最后一前沿应被选入的个数 $K$ ，参考点在前 $l - 1$ 前沿中出现个次数 $\rho_j$ ,距离每个种群个体最小的参考点 $\pi ({\bf s} \in S_t)$ ，种群个体与最近参考点的距离 $d({\bf s}\in S_t)$ ，参考点集合 $Z^r$ 以及最后一前沿种群集合 $F_l$ ;
Ouput: 输出下次迭代种群个体 $P_{t+1}$

（1-2）当最后一前沿种群个体数 $\le K$ 时，执行以下操作：
筛选前 $l - 1$ 前沿中出现次数较少的参考点集合，然后随机选择其中一个种群个体 $\overline j$ ，获取其在参考点中的位置，若在 $l$ 前沿个体中存在 ${\bf s}: \pi({\bf s})=\overline j, {\bf s} \in F_l$ ，则对参考点的出现次数进行操作（操作过程进入第3步）；若不存在，则说明最后一前沿中不存在这样的种群与参考点对应，参考点集中删除此参考点；
若存在此参考点，且参考点的出现次数为0，则选择距离较小的种群个体；若出现次数不为0，则任一选择一个（距离与前边无法对比），然后该参考点被选个数+1，对应的最后一前沿种群个体被选择且被选择个数+1，不再参与后边选择过程。

代码实现

%% Calculate the number of associated solutions except for the last front of each reference point
    rho = hist(pi(1:N1),1:NZ);%除了最后front的每一个参考点，计算关联解的个数 返回每个bin的个数 总共N1个点，散落在NZ个bin中
      %% Environmental selection
    Choose  = false(1,N2);
    Zchoose = true(1,NZ);
    % Select K solutions one by one
    while sum(Choose) < K
        % Select the least crowded reference point
        Temp = find(Zchoose);%索引
        Jmin = find(rho(Temp)==min(rho(Temp)));%所有参考点中与之关联个数最少的那个参考点，一般就是0个，目的是多样性
        j    = Temp(Jmin(randi(length(Jmin))));%随机选择一个参考点最小的参考点
        I    = find(Choose==0 & pi(N1+1:end)==j);% 索引位置是根据现有元素来确定的，可能有多个
        % Then select one solution associated with this reference point
        if ~isempty(I)
            if rho(j) == 0
                [~,s] = min(d(N1+I));%有多个选择最小的那个
            else
                s = randi(length(I));
            end
            Choose(I(s)) = true;%所在的位置
            rho(j) = rho(j) + 1;%个数增加1，也就是说下次再选择它的概率将非常小了
        else
            Zchoose(j) = false;
        end
    end