HDU：1559 最大子矩阵（动态规划DP）

最大子矩阵

Time Limit: 30000/10000 MS (Java/Others)    Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 4132    Accepted Submission(s): 2148

Problem Description

给你一个m×n的整数矩阵，在上面找一个x×y的子矩阵，使子矩阵中所有元素的和最大。

 

Input

输入数据的第一行为一个正整数T，表示有T组测试数据。每一组测试数据的第一行为四个正整数m,n,x,y（0<m,n<1000 AND 0<x<=m AND 0<y<=n），表示给定的矩形有m行n列。接下来这个矩阵，有m行，每行有n个不大于1000的正整数。

 

Output

对于每组数据，输出一个整数，表示子矩阵的最大和。

 

Sample Input

  
  

   
   1
4 5 2 2
3 361 649 676 588
992 762 156 993 169
662 34 638 89 543
525 165 254 809 280
  
  

 

Sample Output

  
  

   
   2474
  
  

 

Author

lwg

 

Source

HDU 2006-12 Programming Contest

 

Recommend

LL

解题思路：

假设在a[5][4]矩阵中求dp[4][3]中长2宽2的子矩阵的元素和（仅仅求元素和，不是最大）

（我们只要求每次求出右下角的子矩阵即可，随着矩阵扩大，答案就会被推算出来）

 

过程：

开始：

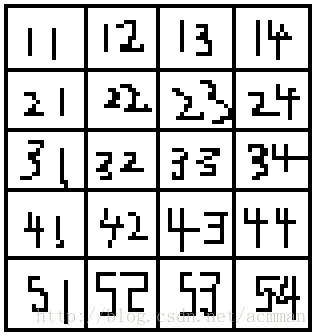
dp[4][3]代表的和

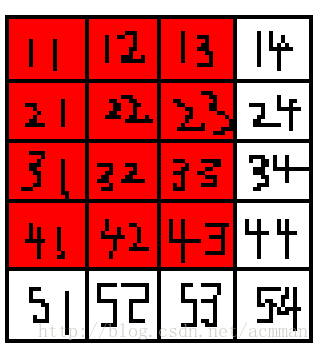
dp[4][1]代表的和

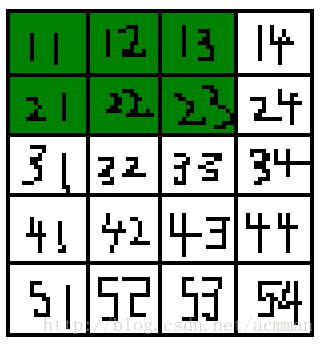
dp[2][3]代表的和

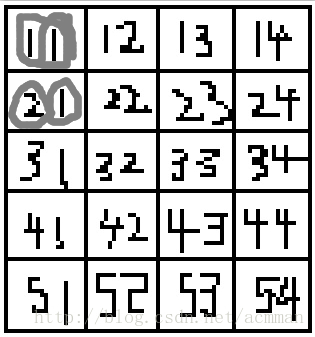
dp[2][1]代表的和

算出dp[4][3]中右下角长2宽2的子矩阵的元素和：

图来自以为前辈学长：http://blog.csdn.net/acmman/article/details/38587897

代码如下：

#include <cstdio>
#include <cmath>
#include <cstring>
#include <queue>
#include <stack>
#include <algorithm>
using namespace std;
int dp[1010][1010];
int main()
{
	int t;
	scanf("%d",&t);
	while(t--)
	{
		memset(dp,0,sizeof(dp));
		int n,m,x,y;
		scanf("%d%d%d%d",&n,&m,&x,&y);
		int ans=0;
		for(int i=1;i<=n;i++)//不从零开始，为下面存dp提供方便 
		{
			for(int j=1;j<=m;j++)
			{
				scanf("%d",&dp[i][j]);
				dp[i][j]+=dp[i-1][j]+dp[i][j-1]-dp[i-1][j-1];//将map[i][j]的左上角所有元素和存起来 
				if(i>=x&&j>=y)//注意这里 
				ans=max(ans,dp[i][j]-dp[i-x][j]-dp[i][j-y]+dp[i-x][j-y]);//以i、j为角标，左上角x*y的矩形之和 
			}
		}
		printf("%d\n",ans);
	}
	return 0;
}