通过高阶DMD对地铁的实时短时OD预测

1. 文章信息

文章题目为《Real-Time Forecasting of Metro Origin-Destination Matrices with High-Order Weighted Dynamic Mode Decomposition》，是一篇发表在Transportation Science上的有关实时地铁OD预测的文章。

2. 摘要

预测不同起点-终点对（即OD矩阵）的短期乘客量对地铁系统的实时运行至关重要。然而，由于OD矩阵的大规模、高维、噪声和高度倾斜的性质，导致OD预测十分困难。文章通过估计低秩、高阶的向量自回归（VAR）模型来解决短期OD矩阵预测问题。文章将这个问题重构为一个数据驱动的降阶回归模型，并使用动态模式分解（DMD）对其进行估计。为了解决地铁OD矩阵无法实时观测的实际问题，文章使用进站需求替换无法获取的OD矩阵。此外，文章还考虑了地铁系统的时间演化特征，并通过指数降低历史数据的权重来改善预测。然后，针对高阶加权DMD模型（HW-DMD），开发了一种定制的在线更新算法，在不存储历史数据或重新训练的情况下，每天更新模型系数。对两个大型地铁系统的数据进行的实验表明，HW-DMD对噪声和稀疏数据具有鲁棒性，在预测OD矩阵和上车流量方面显著优于基线模型。在线更新算法在很长一段时间内也显示出一致的准确性，使我们能够以非常低的成本维护HW-DMD模型。文章的贡献主要为以下三点：

1. 文章提出了一种HW-DMD模型，解决了实时地铁OD矩阵预测的各种困难。实验表明，HW-DMD模型的预测效果明显优于现有模型。

2. 交通系统的时间演化动力学和预测模型的维护/更新在文献中经常被忽略。文章通过减少过去数据的权重来考虑地铁系统的时间演化特性，并显示出改进的性能。为了降低HW-DMD模型在时间演化地铁系统中的长期维护成本，提出了一种在线更新算法。

3. 针对具有外部协变量的大规模高阶向量自回归模型，文章提出了一种基于DMD的估计和在线更新算法。基于DMD的估计为数据生成最佳拟合线性算子，尤其适用于具有低秩属性的高维数据的预测。

3. 问题陈述

许多现代地铁系统使用智能卡记录乘客的进出信息。因此，可以从数据中获取在这样一个系统中每次旅行的起点和终点站，以及开始和结束时间。给定一个固定的时间间隔（本文中为30分钟），文章用表示在第t个时间间隔从i站到j站的行程数，并称为OD流。接下来，通过OD矩阵描述系统中每个OD对在第t个时间间隔内的行程数，其中s代表地铁站点的数目。

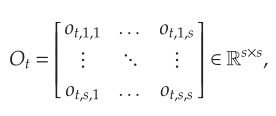
矩阵中对角元素始终为零，文章保留这些零元素，因为它们对预测的影响可以忽略不计。在文章的模型中，OD矩阵以向量形式组织，如下式所示，其中n=s*s。

在文章中，ft也被称之为OD快照。值得注意的是，OD快照是按乘客进入系统的时间进行聚合的；退出时间可能在不同的时间间隔内。因此，只有在以间隔t进入的所有乘客到达目的地后，才能获得间隔t的真实OD快照；无法实时观察（即延迟的数据可用性）。换句话说，在预测ft+1时，通常无法访问ft。相比之下，进站流量是可以实时观察到的。文章用表示时间间隔t内进入i站的乘客数量。文章利用进站客流（进展快照）替换无法获取的OD快照，将OD矩阵预测问题转化为，预测未来的OD快照ft+1、ft+2、ft+L，给定一系列可用的历史OD快照f1、f2、ft和进站快照b1、b2、bt。

4. 模型定义

动态模式分解(Dynamic Mode Decomposition)

动态模式分解（DMD）由流体动力学界开发，用于从高维数据中提取动态特征。文章将OD快照排列成m列矩阵，如下所示，其中m<<n。

线性动力系统遵循Yt≈AYt-1。实际的DMD通过以下程序寻找最佳拟合线性算子A的主要特征值和特征向量。

1.计算Yt-1的截断奇异值分解，如下式所示，其中，。

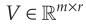2.为了避免计算矩阵A，文章定义了一个新矩阵，如下式所示。

3.计算特征值分解，。

4.DMD模式通过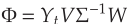获得。

下图，展示了广州地铁10天时间的Yt-1奇异值。可以看到几个前导奇异值解释了很大一部分方差，证实了OD快照数据的低秩特征。因此，基于DMD的模型可以大大降低这种动态系统的维数/复杂性。然而，精确的DMD对于OD流量预测问题有一定的局限性。为了解决这些问题，文章提出了高阶加权的DMD模型。

高阶加权动态模式分解(High-Order Weighted Dynamic Mode Decomposition)

模型说明：

精确DMD的预测公式相当于一阶高维向量自回归。然而，最新的OD快照在预测时是未知的。因此，文章使用的两个最新的进站快照作为替代，认为三个或更多时间间隔前的OD快照可用，这是由于文章所使用的数据集中超过96%的行程在一小时内完成（两个滞后）。文章使用高阶向量自回归来捕捉OD快照中的长期相关性。预测模型如下所示。

进一步，将上式用矩阵形式表示，如下图所示，设m=t-qh。

接着，文章引入了遗忘率ρ（一个介于0-1的数），通过不同的权重给已经过去的时间，以指数方式减少历史数据的权重，从而减小更新参数时内存的占用。上述矩阵形式表示中的Gt可以通过如下优化问题获得。

进一步，为了方便，文章定义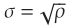，Yt和Xt可以由下式表示。

优化问题(5)也可以改写为最小二乘问题。

至此，可以给出模型的整体框架，如下图所示。

模型估计：

与DMD类似，首先计算的截断奇异值分解，由于部分奇异值就可以很好的表述所有数据，因此可以用于估计系数矩阵，如下所示。

但式(7)与式(9)仍然难以直接进行运算，文章提出寻找一种映射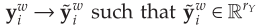：，其中rY<<n。在此过程中，计算目标矩阵的另一秩rY的截断奇异值分解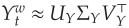。其中Uy的列构成正交基。因此，映射能够将数据映射到一个更低维的空间中，减少了计算量。同样，可以将系数矩阵映射到低维空间中，如下式所示。

至此，可以将模型在一个降阶的子空间中重写，如下式所示。

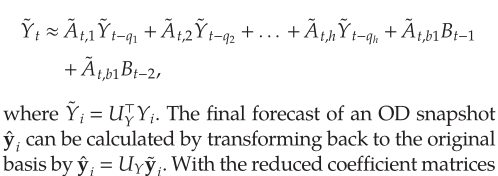
在线更新：

为了阐述在线更新算法，文章进行了如下变量定义。

将公式(7)，也就是稀疏矩阵Gt修改为如下形式。

因此，公式(9)、(10)也可以修改为如下形式。

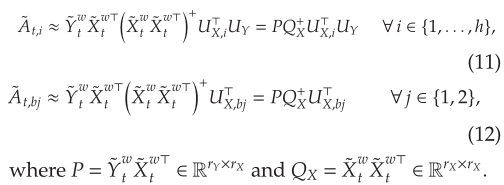
此外，文章定义了一个附加的矩阵，。通过P、Qx、Qy三个矩阵，以及两个投影矩阵Ux、Uy可以表述模型的所有参数。接着，文章给出了两个定理，如下图所示。

定理1用于以节省内存的方式更新核心矩阵。定理2表明，可以使用Qy的特征向量来逼近左奇异向量。根据上述两个定理，在线更新策略分为以下三个步骤：1、扩张投影矩阵Ux、Uy；2、通过定理1更新核心矩阵P、Qx、Qy、Ux、Uy；3、通过定理2对核心矩阵进行压缩、降维。

5. 实验

文章使用广州和杭州两个城市的地铁智能卡数据检查HW-DMD，且文章只关注工作日，并未考虑周末。

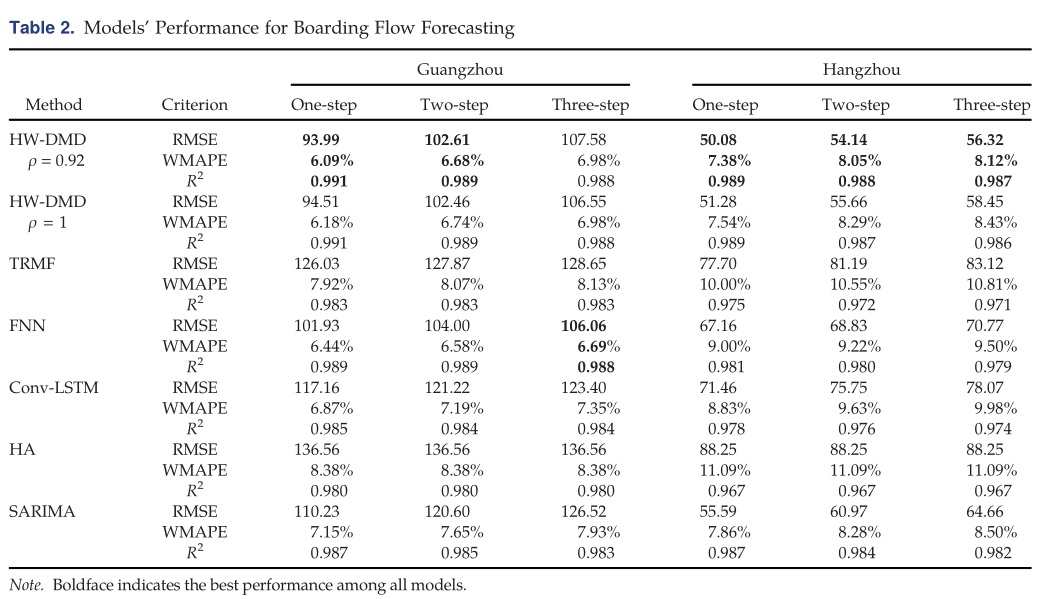
下表展示了OD预测的结果。

下表展示了进站客流预测的结果。

下图中的面板（a）和（c）显示了一天中不同时间的预测RMSE。我们可以看到，HW-DMD的RMSE在大多数时隙中最小，尤其是对于杭州数据集。其他模型，如Conv-LSTM，在清晨和深夜表现稍好，但差异很小，这些时段的总网络OD流量非常小。图中（b）和（d）显示了具有不同流量量级的OD对的预测RMSE。HW-DMD的预测RMSE大大低于高流量OD对的其他模型（平均半小时OD流量大于24）。值得一提的是，OD对的数量随着OD流量的增加呈指数下降，这表明HW-DMD对高度倾斜的数据具有优越的预测能力。

下图展示了广州地铁四个典型OD对OD流量的真实和一步预测。OD流量表现出明显的每日周期性，这解释了为什么HA已经运行良好。与FNN相比，HW-DMD更能预测高流量OD对的波动，如图中的（a）和（b）所示。在（a）中，HW-DMD的预测值通常低于实际值；这是很难避免的，因为在收集真实OD流量时存在两个滞后延迟。系统中的更多OD对类似于中的面板（c）和（d），流量低但噪音高。在如此高的波动性下，HW-DMD的预测反映了平稳的平均值。事实上，其他模型的性能往往会受到噪声的影响。总的来说，HW-DMD在预测和降噪之间取得了很大的平衡，这对于具有不同流量大小的高维系统来说尤其困难。

进一步，文章分析了低秩假设的影响。图中显示了这种低秩近似与原始数据的拟合程度。可以看到，低秩近似为（a）中的高需求OD对保留了大部分信息。相比之下，（b）中稀疏需求OD对中的大多数波动被截断。通过与HA的比较，可以看到，低秩近似反映了稀疏需求OD对的平均日模式，考虑OD对的累积效应时，这是一个合理的近似。因此，秩截断对于过滤大量稀疏需求OD对中的噪声至关重要。

下表进一步定量评估了原始OD数据与其低秩近似值之间的差异。

接着，文章分析了在线更新策略的影响，总结如下。

• 常数模型的RMSE随时间逐渐增加。这表明地铁系统的动态是随时间变化的；因此，预测模型应该定期更新/再训练，以获得更好的性能。

• 在线更新算法的RMSE曲线与每天由整个历史数据重新训练的模型（ρ=0.92）保持一致，表明在线HW-DMD更新算法在长期应用中始终运行良好。对于大型培训集（如图中的9月之后），在线更新方法甚至比再培训略好。

• 适当减少旧数据的权重可以改善预测。比较ρ=0.92与ρ=1。两个再训练的模型；随着训练数据的增加，遗忘旧数据的好处变得更加显著。

• 某些工作日的OD流量可能更难预测，尤其是对9月的预测。周五的RMSE显著高于其他工作日。

6. 总结

文章提出了一种高阶加权动态模式分解（HW-DMD）模型来解决地铁系统的实时短期OD矩阵预测问题。实验表明，在高维、稀疏、噪声和偏斜OD数据下，HW-DMD模型的预测性能明显优于常用的预测模型。文章解决了延迟数据可用性问题和地铁系统的时间演化动力学，这在文献中经常被忽略。在处理时间演化系统时，遗忘率和在线更新的思想也有利于其他预测模型。此外，HW-DMD的实现简单，计算效率高，为一般的高维时间序列预测问题提供了一个有前途的解决方案。

Attention

欢迎关注微信公众号《当交通遇上机器学习》！如果你和我一样是轨道交通、道路交通、城市规划相关领域的，也可以加微信：Dr_JinleiZhang，备注“进群”，加入交通大数据交流群！希望我们共同进步！