赫夫曼树（一）

目录

一.赫夫曼树的基础概念

二.什么是赫夫曼树？

1.案例理解

 2.定义与原理

三.构造赫夫曼树

四.赫夫曼树的实现

---

前言：

在生活中，为了 提高效率，我们做出了很多努力，采取了很多方法。从而节省了很多人力物力，时间资源等。同样在我们传输文件时，我们也需要提高效率。在日常传输文件时我们会采用压缩和解压缩软件来处理文档。因为它除了可以减少文档在磁盘外的空间外，还有重要一点，就是我们可以在网络上一压缩的形式传输大量数据，使得保存和传递都更加高效。

那么压缩而不出错是如何做到的呢？简单来说，就是把我们要压缩的文本进行重新编码，以减少不必要的空间。尽管现在最新技术在编码上已经很好很强大，但这一切都来自于曾经的技术积累，我们今天就来介绍一下最基本的压缩编码方式——赫夫曼编码。

---

一.赫夫曼树的基础概念

赫夫曼（Huffman）树，又称最优树，是一类带权路径长度最短的树。

路径：丛树中一个结点到另一个结点之间的分支构成这两个结点之间的路径。

路径长度：路径上的分支数目称作路径长度。

树的路径长度：从树根到每一个结点的路径长度之和。

树的带权路径长度：树中所有叶子结点的带权路径长度之和。

二.什么是赫夫曼树？

1.案例理解

为方便理解赫夫曼树，我们先用一个简单的例子来理解。现在很多小学学科成绩弃用了百分制的评分方法，而选择用优秀，良好，中等，及格和不及格这样模糊的词来进行评教。在评等级的时候，老师自然不是随心所欲的，而是在成绩出来之后，再统一转换为五级制的成绩。

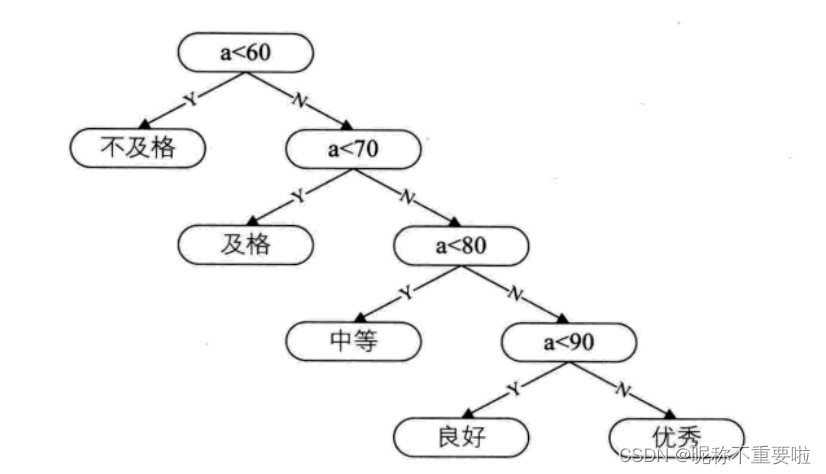
if(a<60)
   b="不及格";
else if(a<70)
   b="及格";
else if(a<80)
   b="中等"；
else if(a<90)
   b="良好"；
else if(a<90)
   b="优秀"；

这样的程序运行过程没有什问题。但是，通常情况下，成绩处于及格，中等，良好的学生数量最多。而上面的程序，就使得所有的成绩都需要先判断是否及格，再逐级而上得到结果。这样的算法效率不高。

我们想办法使得效率更高一些。我们可以选择在出现频率最高的区间段向两边进行判断。

详细如图：

 可以看出成绩出现的最高频率的区间段在80~90区间。我们将这棵二叉树重新分配，如下：

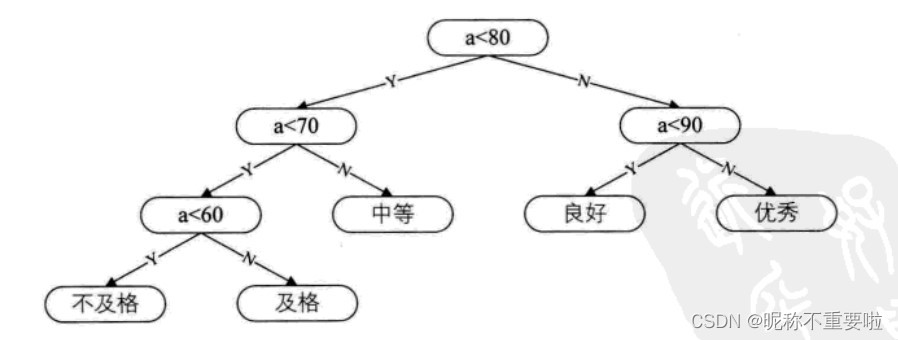
 2.定义与原理

我们先把这两棵二叉树简化为叶子结点带权的二叉树。A：不及格 B：及格 C：中等 D：良好 E：良好。每个叶子上的数字代表五分制每个区间段所占的比例

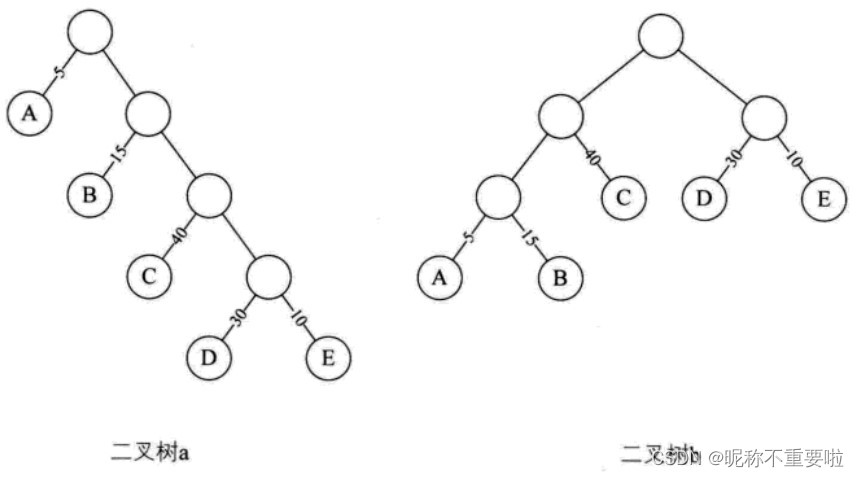
 丛树中一个结点到另一个结点之间的分支构成两个结点之间的路径，路径上的分枝数目称作路径长度。例如：二叉树a中根节点到结点E的路径长度为4，二叉树b中根节点到结点E的路径长度为2。

树的路径长度就是从树根到每一节点的路径长度之和。二叉树a的树的路径长度为：1+1+2+2+3+3+4+4=20。二叉树b的树的路径长度为：1+2+3+2+1+2+2=16。

如果考虑到带权的结点，结点的带权路径长度为从该节点到树根之间的路径长度与结点上权的乘积。树的带权路径长度为树中所有叶子结点的带权路径长度之和。其中带权路径长度WPL最小的二叉树称作赫夫曼树。也称最优二叉树。

根据上述定义，我们来对二叉树a和二叉树b进行带权路径长度的计算。

二叉树a的WPL=5*1+15*2+40*3+30*4+10*4=315

二叉树b的WPL= 5*3+15*3+40*2+30*2+10*2=220

这样的数据表示：如果有10000个学生的百分制成绩需要计算五分制成绩，用二叉树a的判断方法，需要做31500次比较，用二叉树b的判断方法只需要做22000次比较。这样效率就会有很大的提高。

三.构造赫夫曼树

1.先将有权值的叶子结点按照从小到大的顺序排列成一个有序序列； 

2.取头两个最小权值的结点作为一个新结点N1的两个子结点（注意相对较小的是左孩子），新结点的权值为两个叶子权值的和；

3.将N1重新插入有序序列中去，保持从小到大的排序；

4.重复上述操作，完成赫夫曼树的构造。

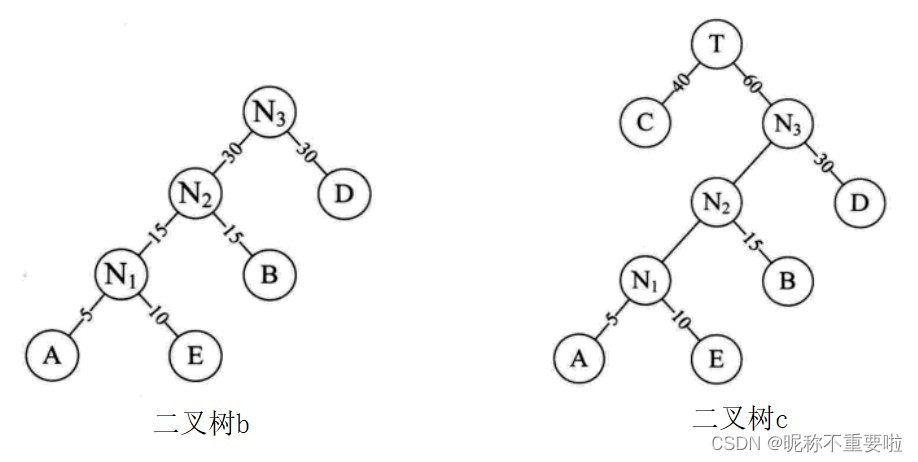
 此时二叉树c的带权路径长度WPL=40*1+30*2+15*3+10*4+5*4=205，相比二叉树b的WPL值220还少了15。此时构造出来的二叉树才是最优二叉树，即赫夫曼树。

四.赫夫曼树的实现

根据上述例子，我们可以得出构造赫夫曼树算法描述：

1.根据给定的n个权值{W1,W2,......,Wn}构成n棵二叉树的集合f={T1,T2,......,Tn}，其中每棵二叉树Ti中只有一个带权为wi根节点，其左右子树均为空。

2.在f中选取两棵根结点的权值最小的树作为左右子树构造一棵新的二叉树，且置新的二叉树的根节点的权值为其左右子树上根节点的权值之和。

3.在f中删除这两棵树，同时将新得到的二叉树加入f中。

4.重复2和3步骤，直到f只含一棵树为止，这棵树便是赫夫曼树。

赫夫曼树代码如下： 

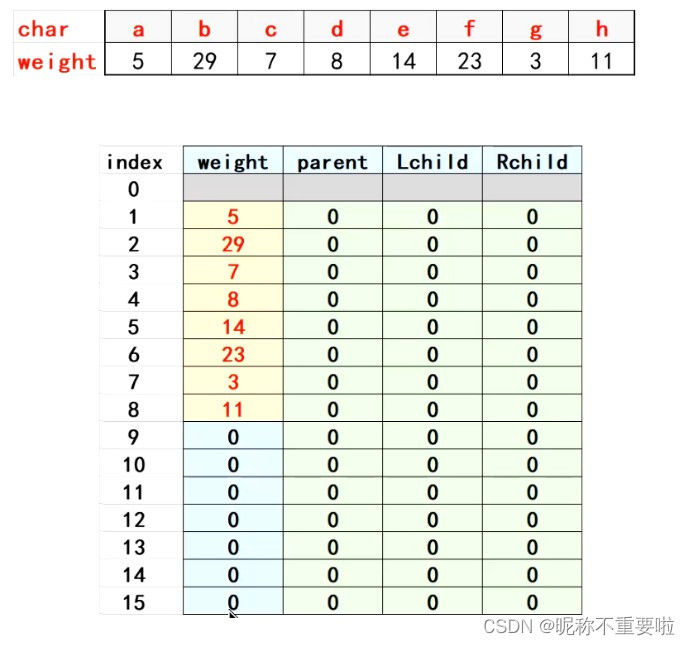
 构建后：

 

#include<iostream>
#include<stdio.h>
#include<string.h>
#include<queue>
using namespace std;

const int n = 8;	 // leaf
const int m = n * 2; // node
typedef unsigned int WeigthType;
typedef unsigned int NodeType;

//赫夫曼树的结点类型
typedef struct
{
	WeigthType weigth;
	NodeType   parent, leftchild, rightchild;
}HTNode;

typedef HTNode HuffManTree[m]; 
typedef struct
{
	char ch;
	char code[n + 1];
}HuffCodeNode;

typedef HuffCodeNode HuffCoding[n + 1];	  // 0// 1- 8 
void PrintHuffManTree(HuffManTree hft)
{
	for (int i = 1; i < m; ++i)
	{
		printf("index %3d weight: %3d parent %3d Lchild %3d Rchild %3d\n",
			i, hft[i].weigth, hft[i].parent, hft[i].leftchild, hft[i].rightchild);
	}
	printf("\n");
}
void InitHuffManTree(HuffManTree hft, WeigthType w[])
{
	memset(hft, 0, sizeof(HuffManTree));
	for (int i = 0; i < n; ++i)
	{
		hft[i + 1].weigth = w[i];
	}
}
struct IndexWeigth
{
	int index;
	WeigthType weight;
	operator WeigthType() const { return weight; }
};
void CreateHuffManTree(HuffManTree hft)
{
	priority_queue<IndexWeigth, vector<IndexWeigth>, std::greater<IndexWeigth> > qu;
	for (int i = 1; i <= n; ++i)
	{
		qu.push(IndexWeigth{ i,hft[i].weigth });
	}
	int k = n + 1;
	while (!qu.empty())
	{
		if (qu.empty()) break;
		IndexWeigth left = qu.top(); qu.pop();
		if (qu.empty()) break;
		IndexWeigth right = qu.top(); qu.pop();
		hft[k].weigth = left.weight + right.weight;
		hft[k].leftchild = left.index;
		hft[k].rightchild = right.index;
		hft[left.index].parent = k;
		hft[right.index].parent = k;
		qu.push(IndexWeigth{ k,hft[k].weigth });
		k += 1;
	}
}
void InitHuffManCode(HuffCoding hc, const char* ch)
{
	memset(hc, 0, sizeof(HuffCoding));
	for (int i = 1; i <= n; ++i)
	{
		hc[i].ch = ch[i - 1];
		hc[i].code[0] = '\0';
	}
}
void PrintHuffManCode(HuffCoding hc)
{
	for (int i = 1; i <= n; ++i)
	{
		printf("data: %c => code : %s \n", hc[i].ch, hc[i].code);
	}
}
void CreateHuffManCode(HuffManTree hft, HuffCoding hc)
{
	char code[n + 1] = { 0 };
	for (int i = 1; i <= n; ++i)
	{
		int k = n;
		code[k] = '\0';
		int c = i;
		int pa = hft[c].parent;
		while (pa != 0)
		{
			code[--k] = hft[pa].leftchild == c ? '0' : '1';
			c = pa;
			pa = hft[c].parent; 
		}
		strcpy_s(hc[i].code, n, &code[k]);
	}
}
//int main()
//{
//	WeigthType w[n] = { 5,29,7,8,14,23,3,11 };
//	char   ch[n] = { 'A','B','C','D','E','F','G','H' };
//	HuffManTree hft = { 0 };
//	HuffCoding hc = { 0 };
//	InitHuffManTree(hft, w);
//	InitHuffManCode(hc, ch);
//	PrintHuffManTree(hft);
//	PrintHuffManCode(hc);
//	CreateHuffManTree(hft);
//	CreateHuffManCode(hft, hc);
//	PrintHuffManTree(hft);
//	PrintHuffManCode(hc);
//
//	return 0;
//}

参考书籍：《大话数据结构  ——程杰》