hiho一下 第五十九周 Performance Log



题目1 : Performance Log

时间限制: 8000ms

单点时限: 1000ms

内存限制: 256MB

描述

You are given a txt file, which is performance logs of a single-threaded program.

Each line has three columns as follow:

[Function Name] [TimeStamp] [Action]

[FunctionName] is a string of length between 1~255

[TimeStamp] format is hh:mm:ss

Valid values for "Action" column are START or END, marking the start or end of a function call.

Each function will only be called once.

Output the depth-first traversal result of the call graph with the total time of each function call. However, sometimes the performance log isn't correct and at that time you just need to output "Incorrect performance log".

输入

The input only contains 1 case, first line is a positive number N representing the number of logs(1 <= N <= 20000), then there are N lines in next, each line is the log info containing [Function Name] [TimeStamp] [Action], [Function Name] is a string, you can assume the [Function Name] is distinct and the length between 1~255.

输出

Output the depth-first traversal result of the call graph with the total time of each function call for the correct performance, or output "Incorrect performance log".

提示

A call graph is a directed graph that represents calling relationships between subroutines in a computer program.

Call graph for the sample input is shown as below:

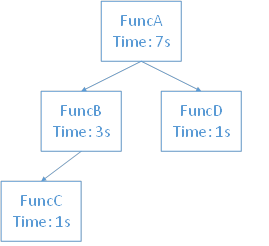
Another sample test case.

Sample Input	Sample Output
8 FuncA 00:00:01 START FuncB 00:00:02 START FuncC 00:00:03 START FuncA 00:00:04 END FuncB 00:00:05 END FuncD 00:00:06 START FuncD 00:00:07 END FuncC 00:00:08 END	Incorrect performance log

样例输入

8
FuncA 00:00:01 START
FuncB 00:00:02 START
FuncC 00:00:03 START
FuncC 00:00:04 END
FuncB 00:00:05 END
FuncD 00:00:06 START
FuncD 00:00:07 END
FuncA 00:00:08 END

样例输出

FuncA 00:00:07
FuncB 00:00:03
FuncC 00:00:01
FuncD 00:00:01

 

题意分析

给定一个单线程程序运行的记录，包含有每个函数启动和结束的时间。判定该份记录是否错误，主要的错误包含：

• 记录中的时间不是严格递增的
• 一个函数的结束时间比启动时间更早
• 记录中一个函数有不对应的启动操作START或结束操作END，比如出现了START却没有对应的END，或出现了END却没有出现START。而函数的START和END应该成对出现
• 两个函数出现交叉的情况，而在单线程程序中是不会出现的，比如A START B START A END B END

算法分析

根据上面对可能出现错误的分析，我们可以分别对每一种错误进行处理：

记录中的时间不是单调递增的

对每一条记录的时间都与前一条的时间进行比较即可判定。

一个函数的结束时间比启动时间更早

对出现的START和END标记的时间直接进行计算即可判定。

不对应的START和END

统计每个函数START和END的个数是否相等即可判定

两个函数出现交叉

本题要做的是模拟一个函数调用栈，其实际考察的内容是对于栈的理解和运用。

我们将函数启动的操作视为进栈PUSH，函数结束的操作视为出栈POP，对于一个单线程的程序来说，其函数的调用一定满足栈的过程。在出现函数A中调用函数B的情况时，函数B的结束时间一定早于函数A。这正是栈过程中先进后出原则的体现。

如果我们用栈来模拟前面的例子，则有

• A START

  Stack A

• B START

  Stack A B

• A END

  此时出现了错误，其操作为不在栈顶的A出栈。

对于正确的情况，比如：

A START B START B END A END

同样用栈来模拟时有：

• A START

  Stack A

• B START

  Stack A B

• B END

  Stack A

• A END

  Stack

因此对于第三类错误，我们需要在程序中使用栈来模拟整个过程，即可判定是否有出现错误。

总结

我们使用栈来模拟整个程序调用的过程：

首先对于每一个记录比较与前一条记录的时间。

当出现了START操作的函数直接进栈。

当出现了END操作的函数时，判定该函数是否就是栈顶的函数，若不是则表明该记录有错误。同时对于第二类操作中"出现了END却没有出现START"的情况也处理了。若出栈元素是栈顶元素时，我们在此时对其时间进行一次检查，就可以判定第一类错误。

当整个过程记录都使用栈模拟完毕后，我们还需要对当前栈内是否还有元素进行判定。若栈不为空，则出现第二类情况中"出现了START却没有对应的END"的情况。

此外在输出时，题目要求按照函数调用树深度优先的顺序依次输出每一个函数。在模拟栈的过程中，函数入栈的顺序也正是调用树的顺序，所以在处理过程中我们使用一个序列outputList来记录函数入栈的顺序，并在函数END操作时去更新该函数其运行时间。

其伪代码如下：

For i = 1 .. n
    If (i != 0 and log[i].time < log[i - 1].time)
        Return "Error"
    End If
    If log[i].Action == "START" Then
        Stack.Push(log[i])
        outputList.push(log[i].FuncName)    // 将该函数压入输出序列
    Else
        If (Stack.Size == 0 or Stack.Top.FuncName != log[i].FuncName)
            Return "Error"
        End If
        startLog = Stack.Pop()
        If startLog.Time > log[i].Time Then
            Return "Error"
        End If
        setTime(startLog.FuncName, log[i].Time - startLog.Time)
        // 记录outputList中名称为startLog.FuncName的函数的运行时间
    End If
End For

结果分析

在实际的比赛中，该题目的通过率为14%。

在选手的程序中主要出现的错误有：

• 由于本题涉及了时间格式，在时间输入输出上出现问题，导致时间计算出问题
• 未判定函数开始时间是否大于结束时间
• 模拟栈结束后未检查栈是否为空，很多选手都是因为这个原因而没有得到100分

很不赖的一道题！！

#include <iostream>
#include<cstdio>
#include<cstring>
#include<stack>
using namespace std;
struct Log
{
    char FuncName[260];
    int Time;
    char time[10];
    char Action[20];
};
Log log[20000+5];
Log log1[20000+5];
int n,k=0;
stack<Log> Stack;
void printTime(int t)
{
    int ss=t%60;
    t=t/60;
    int mm=t%60;
    t=t/60;
    int hh=t%60;
    printf("%02d:%02d:%02d\n",hh,mm,ss);
}
void setTime(char name[],int t)
{
    for(int i=1;i<=k;i++)
    {
        if(!strcmp(log1[i].FuncName,name))
            log1[i].Time=t;
    }
}
int main()
{
    scanf("%d",&n);
    for(int i=0;i<n;i++)
    {
        scanf("%s%s%s",log[i].FuncName,log[i].time,log[i].Action);
        log[i].Time=(log[i].time[0]*10+log[i].time[1])*3600+(log[i].time[3]*10+log[i].time[4])*60+log[i].time[6]*10+log[i].time[7];
    }
    /*
    for(int i=0;i<n;i++)
        printf("%s%d%s\n",log[i].FuncName,log[i].Time,log[i].Action);
    */
    int flag=0;
    if(!strcmp(log[0].Action,"START"))
        strcpy(log1[++k].FuncName,log[0].FuncName);
    Stack.push(log[0]);
    for(int i=1;i<n;i++)
    {
        if(log[i].Time<log[i-1].Time)  //时间没有递增
        {
            flag=1;
            break;
        }
        else
            if(!strcmp(log[i].Action,"START"))
            {
                strcpy(log1[++k].FuncName,log[i].FuncName);
                Stack.push(log[i]);
            }
            else
            if(!strcmp(log[i].Action,"END"))
            {
               Log ll=Stack.top();
               if(strcmp(log[i].FuncName,ll.FuncName) || log[i].Time<ll.Time)
               {
                   flag=1;
                   break;
               }
               else
               {
                   Stack.pop();
                   setTime(ll.FuncName,log[i].Time-ll.Time);
               }
            }
    }
    if(flag || Stack.size()) printf("Incorrect performance log\n");
    else
    {
        for(int i=1;i<=k;i++)
        {
            printf("%s ",log1[i].FuncName);
            printTime(log1[i].Time);

        }
    }
    return 0;
}