2014年某大型互联网国企北航宣讲时的笔试（行测类型的题）

缘由

上周参加的某大型国企的宣讲会和笔试，这是笔试题。无论是什么方向的都会需要考这套题，所以与it没有太大关系。有点类似于行测。

第一题

2月28日出生和2月29日出生的人的比例是多少？2012年2月28日和2012年2月29日出生的人的比例是多少？

A.       1:1和1:1

B.      4:1和1:1

C.      1:1和4:1

D.       4:1和4:1

标准解答

和我的说法一样

我的解答

显然2月29日是每四年出现一次。所以是4:1。而2012年2月28日和2012年2月29日，这个是已经固定的了。可以视为平常日子里面的任意两天。所以出生孩子的比例应该是1:1

 

第二题

某连锁企业在10个城市共有100家专卖店，每个城市的专卖店数量都不同。如果专卖店数量排名第5多的城市有12家专卖店，那么专卖店数量排名最后的城市，最多有几家专卖店？

A. 2

B. 3

C. 4

D. 5

标准解答

本题选择C。这是一道最值问题，可采用方程法，设专卖店数量排名最后的城市最多有x家专卖店，要使得专卖店数量排名最后的城市的专卖店的数量最多，则排名前5的城市的专卖店数量应尽量少，分别为16,15,14,13,12,而排名后5的城市的专卖店数量为X+4，x+3，x+2，x+1，x，则根据题意得：16+15+14+13+12+x+x+1+x+2+x+3+x+4=100,解得x=4，因此答案选择C选项。

我的解答

根据第五多的城市有12家。那么第四多的城市至少是13家。以此类推。我们需要知道最后一个城市最多有多少家。那么我们就让前面9个城市的专卖店的店数最少。前1到5年各是16到12。100-(16+15+14+13+12)=30，而后6到10是总共30家。 如果第10家是x，第9家也必须必第10家多一个，才能保证第10家最多（此时符合题意）。5x+1+2+3+4=30。固得x=4。

1    2    3    4    5    6    7    8    9    10

16  15  14  13  12  x+4 x+3 x+2 x+1 x

 

第三题

烧杯中装了100克浓度为10%的盐水，每次向该烧杯中加入不超过14克浓度为50%的盐水，问最少加多少次之后，烧杯中的盐水浓度能达到25%？（假设烧杯中盐水不会溢出）

A.6 

B. 5  

C. 4

D.3

标准解答

假设最少加入M次，根据溶液混合前与混合后溶质的量保持不变，可得：100×10%＋14M×50%≥（100＋14M）×25%，解得M≥30/7，因此最少加入5次。

我的解答

设为x次。总共加入的盐：x*14*0.5。杯中有100*0.1。而水呢？加入的水也是x*14*0.5，杯中有水：100*0.9。

 (x*14*0.5+100*0.1)/( x*14*0.5+100*0.9)=0.25

求出x=2.38。没有算出答案。看了标准答案之后再说吧

感悟：上面的计算错误在于浓度的计算。应该是溶质除以溶质加溶液的质量。
(x*14*0.5+100*0.1)/( x*14+100)=0.25

X=4.28所以要五次。

 

第四题

在一本300 页的书中，数字“1”在书中出现了多少次？

标准解答

与我的解法类似。

我的解答

首先100-199是肯定出现了100个1了（百位数）。下面的难点在于0到99。那么10到19。只算十位的话有是10个1。而1、11、21、31、41、51、61、71、81、91只看个位的话只有9个（明明是十个）。所以我觉得0到99应该19个。3个19再加上百位的100到199为接近于答案的160。但是我好像忽略了一个。忽略的后来找到了。

 

第五题

4个袋子，15个球，每个袋子至少放一个球，而且袋子中的球数量不能重复，有多少种方式？

A.4

B.5

C.6

D.7

标准解答

也就是穷举，每个袋子的个数：
1,2,3,9      

1,2,4,8      

1,2,5,7      

1,3,4,7      

1,3,5,6      

2,3,4,6      

我的解答

这道题我就已经不太知道怎么做了。我就穷举了一下。

因为每个袋子至少放一个。那么假设每个袋子已经被放了一个，那么这个问题就是成了每个袋子里放11个的问题。

11  0    0    0

10  0    0    1

8    0    1    2

7    1    2    3

我只能穷举出这四种。

感悟

是微软的校招笔试题，太不小心了，居然没有穷举完。

第六场

小组赛，每个小组有5支队伍，互相之间打单循环赛，胜一场得3分，平一场得1分，输一遍不得分，小组前三名出线，平分抽签，一个队最少拿几分就有理论上的出线希望？

标准解答

出线需要淘汰两支队伍。

理论上只要两分就有抽签出线的希望：

假设五支队伍为A、B、C、D、E

A、B、C三支队伍相互都是平局，他们全都负于D队及E队。这样ABC三队都是两分，平分抽签，就有了理论上的出线希望。

只得一分是不可能出线的，因为负了三场，则有三支队已经至少三分了，只取前三名，得一分不可能出线。

我的解答

当时考场上脑子一团浆糊，现在好点了。我们从答案给出的4个选项来推测。

一分就是该队平1输3，那么赢他的3个队都已经累积3分，已经出线了，所以不是一分。

两分就是平二输二，那么，作为第三名，他平了第四名和第五名，输给了前第一名和第二名。但是第四名和第五名之间的比赛如果都平了，就是有3个队伍是2分。如果第五名或者第四名谁赢了的话，那么就是已经是4分了。所以占了出线的名额。

如此看来三分就有很大的可能了。三分就是平三输一或者赢一输三。如果是平三输一的话，就算只输给了第一名。那么第五名和第四名只要他们之间的比赛平了，就最多只能得到2分。（其中一份来自和第三名的比赛平了）

感悟

我居然忽略了评分就抽签

第七场

本届世界杯决赛有有六名乒乓球选手进行单打循环赛，比赛在三个台上同时进行，比赛时间是每星期六的下午，每人每周只能而且必须参加一场比赛，因而比赛需要进行五周。已知在第一周的星期六王励勤和张继科对垒；第二周马琳与马龙对垒；第三周王皓和王励勤对垒；第四周马龙和张继科对垒。当然，在上述这些对垒的同时，另外还有两台比赛，但这两台比赛是谁和谁对垒，我们不清楚。问：上面未提到过名字的郝帅在第五周同谁进行了比赛?

标准解答

先考虑王励勤在各周都是同谁进行了比赛，已知在第一周王励勤同张继科，第三周王励勤同王皓进行比赛，因而王励勤同马龙、马琳、郝帅的比赛只能分别在第二、四、五周了，但由于第二周马龙同马琳对垒，因而这一周王励勤就只可能同郝帅比赛了，同理可推得在第四周王励勤同马琳，第五周王励勤同马龙对垒，其次考虑马龙在各周都是同谁进行了比赛，用同样的分析方法可推知第一周马龙同王皓，第二周马龙同马琳，第三周马龙同郝帅，第四周马龙同张继科，第五周马龙同王励勤对垒，有了这个结果下面的问题就迎刃而解了，由于每周都有三台比赛，知道了其中两台选手，另一台的两位选手自然就不难推出，由此推得在第五周郝帅同张继科进行了比赛

我的解答

该题的名字比较容易扰乱思维，所以将名字换成A、B、C、D、E、F。对应关系如下：

A         B         C         D         E          F

王励勤        张继科        马琳           马龙           王浩           郝帅

      已知

第一周：A-B           C D E F F- C、E-D。因为C-D在第二周举行

第二周  ：C-D         AB E F       A-F、B-E因为A-B在第一周打、E-A在第三周打

第三周：E-A      B C D F F-D、C-B

第四周：D-B           A C E F       F-E、A-C必须在第二周打。

第五周：F-? 只剩下B

所以选张继科。

感悟

答案应该还没有我的思路清晰

第八场

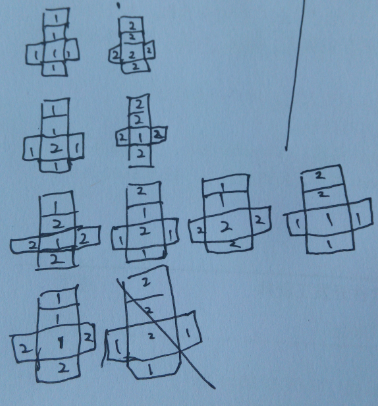
设想你有一罐红漆，一罐蓝漆，以及大量同样大小的立方体木块。你打算把这些立方体的每一面漆成单一的红色或单一的蓝色。例如，你会把一块立方体完全漆成红色。第二块，你会决定漆成3面红3面蓝。第三块或许也是3面红3面蓝，但是各面的颜色与 第二块相应各面的颜色不完全相同。

按照这种做法，你能漆成多少互不相同的立方体? 如果一块立方体经过翻转，它各面的颜色与另一块立方体的相应各面相同，这两块立方体就被认为是相同的。

标准解答

我的解答

穷举所有的情况，注意穷举的时候的规律。

感悟

我认为答案错了。但是因为3面红3面蓝，其实只有一个。

 

第九题

100个人回答五道试题，有81人答对第一题，91人答对第二题，85人答对第三题，79人答对第四题，74人答对第五题，答对三道题或三道题以上的人算及格， 那么，在这100人中，至少有（ ）人及格。

标准解答

问至少有多少人及格，那就是说不及格的人数最多时及格的人数最少．100人回答5道题，相当于做500道题，共答对的题目数量有：81+91+85+79+74=410（道），则出错的数量有：500-410=90（道），错3道以上就不及格，每人错3道时不及格人数最多，90÷3=30（人），则及格的人数是：100-30=70（人）。如果每人错五道，则为不及格的人最少。90÷5=18（人）。将会有82人及格，这是最多的情况。

我的解答

我没有想出完整的推理的过程，但是我发现如果答对第五题的74个人，同时也答对了第一、二、三、四题。这种的情况完全可以出现，但是这好像不是最少的情况。

感悟

错得一塌糊涂

第十题

某公司针对A、B、C三种岗位招聘了35人，其中只能上B岗位的人数等于只能上C岗位人数的2倍．而只能上A岗位的人数比能兼职别的岗位的人多1人，在只能上一个岗位的人群中，有一半还能上A岗位，则招聘的35人中能兼职别的岗位的有多少人．

A.10

B.11

C.12

D.13

标准解答

根据题干，设能兼职的有X人，则只能上A岗位的有X+1人，又设只能上B岗的有Y人，则只能上C岗的有2Y人，由此即可得出两个关于X、Y的二元一次方程：X+1+Y+2Y+X=35，X+1=Y+2Y；利用代入消元法消去未知数Y，即可求得X的值．

解答：解：设能兼职的有X人，则只能上A岗位的有X+1人，又设只能上C岗的有Y人，则只能上B岗的有2Y人，根据题意可得方程：

X+1+Y+2Y+X=35，

X+1=Y+2Y，

整理可得：X+3Y+1=35，①；

3Y=X+1，②；

把②代入①可得：

3X=33，则X=11，

答：招聘的35人中能兼职别的岗位的有11人．

故答案为：11．

我的解答

设A、B、C、M分别代表只能担任A、B、C岗位和能够兼职的人。所以可以根据答案倒推。

A    B+C     M

11  共11    10  不符合题意，因为加起来不是35

12  共12    11  符合题意加起来35.

 

第十一题

A、B、C、D、E是5个不同的整数，两两相加的和共有8个不同的数值，分别是17、25、28、31、34、39、42、45，则这5个数中能被6整除的有几个？

A.0

B.1

C.2

D.3

标准解答

【正确答案】C

方法一：设五个整数从小到大依次是A、B、C、D、E，五个数两两相加的和应有10个，分别为

A+B,A+C,A+D,A+E,

B+C,B+D,B+E,

C+D,C+E,

D+E；

由于“两两相加的和共有8个不同的数值”，故定有两个数值重复出现过。

分析可知，A+B和A+C分别是数值最小的两个数，即A+B=17,A+C=25；

C+E和D+E分别是数值最大的两个数，即C+E=42,D+E=45。

并且这四个数字是不能重复的，即重复出现的数字一定是在28、31、34、39

五个整数两两相加的和一定满足能被4整除（每个数都加了四遍）。

而题目中两两相加得出的8个不同数值的和为261，除以4余数为1，那么重复出现的两个数的和除以4一定余3。

28、31、34、39中只有28+31=59与28+39=67两个数除以4，余3，故数字28一定是重复出现的数字。

由于28是第三大的数字，可推知B+C=A+D=28,联立A+C=25，可知B-A=3,再联立A+B=17，可知A=7,B=10。同法可依次解得C=18,D=21,E=24。五个数字中能被6整除的有两个，故选择C选项。

方法二：五个数字两两相加，得出的八个和中有5个是奇数，有3个是偶数，可以推论这五个数字中奇数个数必为两个或者三个。（如果只有一个奇数，那么加和最多只能出现4个奇数；如果有4个奇数，那么加和最多只能出现4个奇数；如果有5个奇数，那么加和不可能出现奇数）即五个数字中要么有三个奇数，要么有三个偶数。只有同奇同偶数字相加时，和才能为偶数，故28、34、42三个数必为三个同奇同偶数字两两相加的和。设三个同奇同偶数字分别A、B、C，则有2×（A+B+C）=28+34+42，即A+B+C=52，从而可以分别解出三个同奇同偶数字分别为52-28=24，52-34=18，52-42=10。三个数字中有两个数字能被6整除，剩余两数定为奇数，定不能被6整除，故能被6整除的数字共有2个。故应选择C选项。

方法三：设五个整数从小到大依次是A、B、C、D、E，五个数两两相加的和应有10个，分别为

A+B,A+C,A+D,A+E,

B+C,B+D,B+E,

C+D,C+E,

D+E；

分析可知，A+B和A+C分别是数值最小的两个数，即A+B=17,A+C=25；

C+E和D+E分别是数值最大的两个数，即C+E=42,D+E=45。

数值28可能为A+D的和，也可能为B+C的和；

数值39可能为B+E的和，也可能为C+D的和。

可推断5个数的奇偶性，

当A为奇数时，奇偶性如下： 当A为偶数时，奇偶性如下

A B C D E A B CD E

奇 偶 偶 奇 偶 偶 奇 奇 偶 奇

经观察可知，无论何种情况B与E必定同奇或同偶，即B+E≠39。故C+D=39。

联立C+E=42,D+E=45,C+D=39，易求E=24，

从而可分别求出A=7,B=10,C=18,D=21,E=24

有C、E两个值可被6整除，故应选择C选项。

我的解答

不仅解题思路错了，连标准答案都不想看懂了。

将能被6整除的数举例出来：6、12、18、24、36、42，再多就大于题中两两相加的数字了

17 25 28 31 34 39 42 45   

如果有6      11 19 22 25 28 33 36 39   不行

如果有12    5  13  2619 22 27 30 33     不行

显然这样做不出来，因为6只和其中4个数相加，而不是8个。但是我不知道是哪四个。

后来又想到一种解法，那就是两个能被六整除的人的和肯定也是能被六整除的。这里面只有一个42。42/6=7

所以可能的组合就是

6    12  24

6    36

再考察两组最大的数，如果36的话，那么36与别的数相加时，必定会产生4个比36大的数，但是实际只有3个比36大的数。

如果是24的话，题中应该会有24+12=36。但是又没有，所以我觉得可以排除C、D选项。那么就只有A、B选项了。

假设有一个，那么范围也就是在6、12、18、24、36、42中的一个。42、36、6都排除，42和36、6排除的原因和上面类似（如果36的话，那么36与别的数相加时，必定会产生4个比36大的数，但是实际只有3个比36大的数）。那么就只剩下12、18、24了。接着我就判断不了。

 

第十二题

一群猴子采摘水蜜桃。猴王不在的时候，一个大猴子1时可摘15kg，一个小猴子1时可采11kg；猴王在监督的时候，大猴子的1/5和小猴子的1/5必须停止采摘，去伺候猴王。有一天，采了8小时，其中第一小时和最后一小时有猴王在场监督，结果共采3382kg的水蜜桃，在这个猴群里共几只大猴子?

A.10

B.13

C.14

D.15

标准解答

时间：8小时

猴王在：2小时

猴王在时效率：80%

设每小时采xkg水蜜桃

6x+80%*2x=3382

x=445

猴王不在时，每小时445kg

设大的y只，小的z只

11z+15y=445

正整数解为：大4小35

大15小20

大26小5

我的解答

可以列出算式，然后猴子的个数必为整数。我列的算式如下图。

第十三题

A与B两山村之间的路不是上坡就是下坡，相距60千米。邮递员骑车从A村到B村，用了3.5小时；再沿原路返回，用了4.5小时。已知上坡时邮递员的车速是12千米/小时，则下坡时邮递员的车速是？

A、10千米/小时 B、12千米/小时 C、14千米/小时 D、20千米/小时

标准解答

D。解析：方法一，如下图：
可以看图知道无论道路怎么样去是上坡的回来必是下坡，反之，去是下坡的回来必是上坡，从而知道一个来回上坡、下坡均有60千米，又由题意可知往返共花了3.5+4.5=8小时故上坡用时60÷12=5小时，下坡用时8-5=3小时，下坡速度就是60÷3=20千米/时。
方法二，共120千米花了8小时，平均每小时120/8=15千米每小时，下坡一定比平均速度大，故选比15大的D选项。

我的解答

显然下坡速度要快于上坡速度嘛，所以就选C或者D。然后再假设是C，带入公式进入计算就会发现，算出来的结果是负数。

假设从A到B的时候，上坡时间t1、下坡时间t2

t1*12+14*t2 = 60

t1+t2=3.5

两个方程解两个未知数，t1会为负数（如果我没算错的话），所以选D。

感悟：原来这些题根本不需要多少时间，如果你会做的吧。

 

第十四题

两人做一种游戏：轮流报数，报出的数只能是 1， 2， 3， 4， 5， 6， 7， 8.把两人报出的数连加起来，谁报数后，加起来的数是 123，谁就获胜，让你先报，就一定会赢，那么你第一个数报几？

标准解答

123/9=13……6

所以第一个报6

然后不管对方报几，你就报9-几

比如，对方报1，你就报8

对方报5，你就报4。这样必赢

我的解答

做不出来。

感悟

标准答案解的太秒了。题中有个暗示就是只能报1-8的数。那么对方无论报多少都可以报与9的差，这样就不怕对方乱报了。