主成分分析法的SPSS操作

最新推荐文章于 2024-05-09 16:30:28 发布
最新推荐文章于 2024-05-09 16:30:28 发布
阅读量1.4w 收藏 317
点赞数 12
文章标签： 大数据
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.csdn.net/zyq357/article/details/113617071
版权

将数据导入到SPSS中
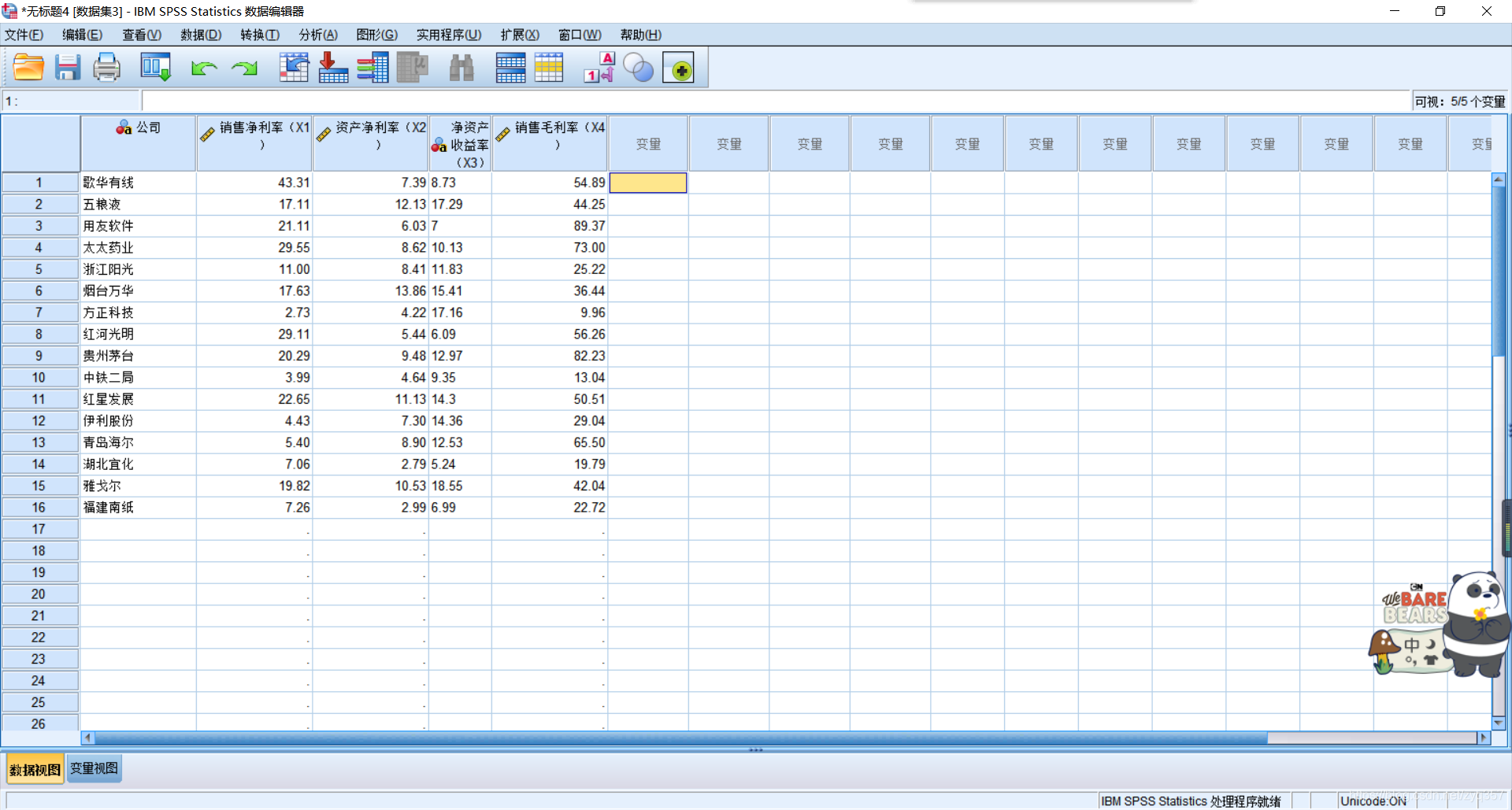
在这里插入图片描述
确定变量类型正确
在这里插入图片描述
进行标准化处理，点击上方菜单栏分析——描述统计——描述
在这里插入图片描述
将变量全部选入，并勾选将标准化值另存为变量
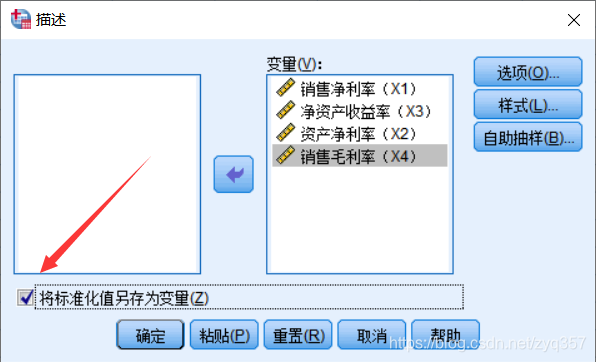
在这里插入图片描述
随后点击分析——降维——因子
在这里插入图片描述
对描述进行修改
在这里插入图片描述
载荷图可选也可不选
在这里插入图片描述
得分中选中保存为变量和显示因子得分系数矩阵
在这里插入图片描述
设置完成，得到想要的结果
在这里插入图片描述
通过总方差解释表分析，可以看到前两个成分的值大于了85%，所以前两个就为主成分
在这里插入图片描述
通过分析成分矩阵，可知，第一主成分主要和销售净利率、资产净利率、销售毛利率有关，第二主成分主要和净资产收益率有关
在这里插入图片描述
因为目前得到的是因子的载荷矩阵，并不是主成分分析的载荷矩阵，所以还需进行处理
点击复制数据
在这里插入图片描述
随便命个名，叫v1,v2
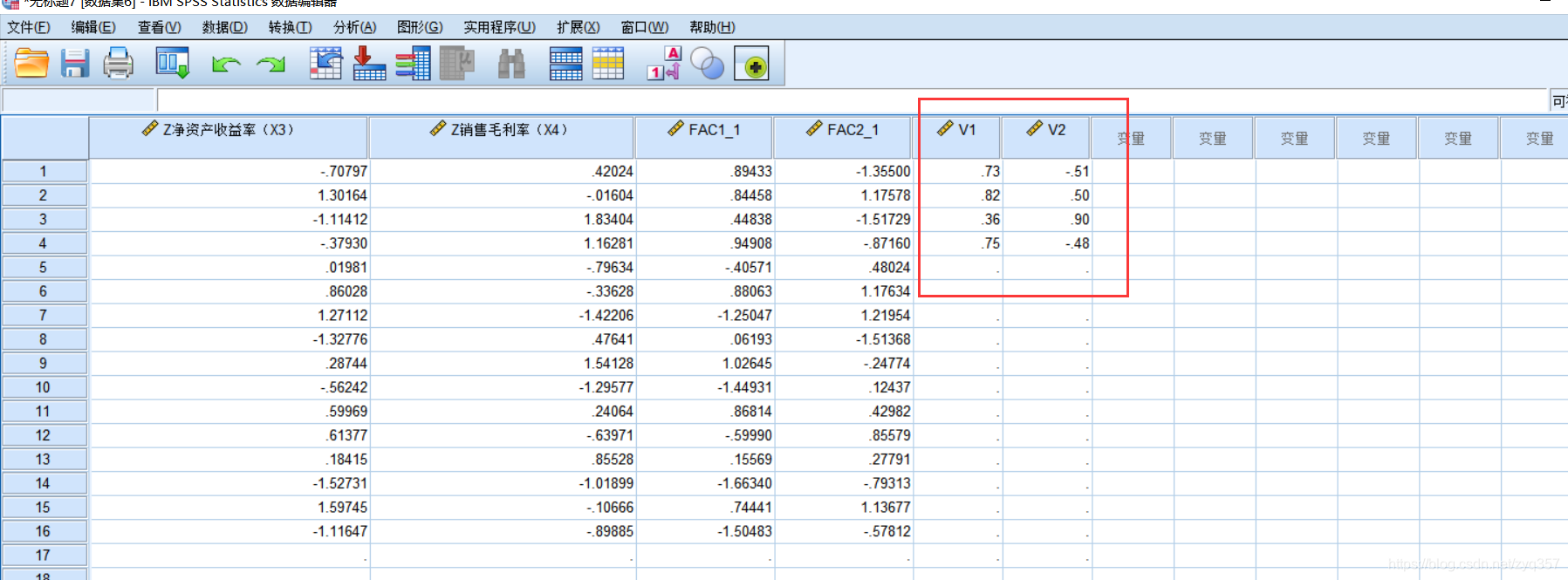
在这里插入图片描述
点击计算变量
在这里插入图片描述
需要除以根号λ，就可得到最新的特征向量
在这里插入图片描述
在这里插入图片描述
例如得到的数据w1也就是最终的系数u11、u12、…u1p 等。
在这里插入图片描述

那么通过公式计算最终也就可得到指标值
在这里插入图片描述
在这里插入图片描述

最终由四个指标变为了两个指标，起到了降维的效果
在这里插入图片描述

咏琪小同学
关注
  • 12
    点赞
  • 踩
  • 317
    收藏
    觉得还不错? 一键收藏
  • 1
    评论
SPSS（十一）SPSS信息浓缩技术--主成分分析、因子分析（图文+数据集）
可乐联盟
05-26 2万+
SPSS（十一）信息浓缩技术--主成分分析、因子分析（图文+数据集） 当我们的自变量存在多重共线性，表现为进行回归时候方程系数估计不正常以及方程检验结果不正常，也许我们可以使用变量挑选的办法（手动挑选、向前法、向后法、逐步法），但是再复杂一点其实就不行了，之前我们介绍过岭回归解决该问题，其实我们还可以使用信息浓缩的技术来解决自变量存在多重共线性问题。 本讲课程中涉及的方法其实质均为数据化简、信...
[统计学笔记] 方差分析表的解读
热门推荐
梅森上校的博客 业精于勤荒于嬉，形成于思毁于随。
04-23 5万+
方差分析表的解读 方差分析表(analysis of variance table)是指为了便于进行数据分析和统计判断，按照方差分析的过程，将有关步骤的计算数据，例如差异来源、离差平方和、自由度、均方和F检验值等指标数值逐一列出，以方便检查和分析的统计分析表。 利用 Excel 中数据分析的功能可以快速构造出方差分析表。 方差分析表（Analysis of variance table）可以...
因子分析（SPSS和Python）
m0_67790374的博客
10-12 1万+
分别通过SPSS和Python进行因子分析
SPSS之主成分分析
最新发布
__forward--的博客
05-09 2017
PCA主成分分析方法，是一种使用最广泛的数据降维算法。PCA的主要思想是将n维特征映射到k维上，这k维是全新的正交特征也被称为主成分，是在原有n维特征的基础上重新构造出来的k维特征。
SPSS主成分分析
stone_tigerLI的博客
10-28 2829
原始数据 点击分析(analyze)——降维(dimension reduction)——因子分析(factor)，将需要参与分析的各个原始变量放入变量框， 如图所示 点击描述 点击得分 点击抽取 点击选项 点击确定，结果如下 相关性矩阵 KMO和Bartlett球形检验结果： KMO为0.6，说明适合做因子分析； bartlett球形检验的显著性P值为0.000<0.05，亦说明数据适合做因子分析。 公因子方差表，展示了变量的共同度，提取下面各个共同度的值都大于0.5，说明提取的
主成分分析——SPSS实例分析
qq_52862974的博客
06-18 2476
主成分分析是用原始变量的线性组合来表示主成分，且主成分彼此之间互不相关，且能反映出原始数据的绝大部分信息。 一般来说，当研究的问题涉及到多变量且变量之间存在很强的相关性时，我们可考虑使用主成分分析的方法来对数据进行简化。SPSS 软件中主成分分析与因子分析均在“因子分析”模块中完成。因此，在 SPSS 数据表中录人以上数据后，依次点击“分析-降维-因子”进入“因子分析”对话框，然后将12个变量全部选入“变量”框中。
手把手教你做主成分分析
m0_37228052的博客
09-02 4982
这表示，第一主成分可解释我们待降维的7个指标50.266%的信息量，第二主成分可解释23.512%的信息量，第三主成分可解释14.954%。如果是强调主成分命名，那么这样的载荷是不利于命名的。根据特征根，可以计算每个主成分的方差贡献比例（或称之为方差解释率，下同），特征根，方差解释率是我们判断主成分个数的核心依据。主成分或因子分析用作综合评价研究，最后一步主要是基于主成分或公因子得分数据，以及构造的综合得分数据，对研究对象进行排名，根据各得分数据、排名的表现展开对研究对象的评价工作。
主成分分析_spss_主成分分析_
10-04
根据数据进行主成分分析，剔除不符合的数据。
SPSS13.0主成分分析详细操作步骤
07-27
在数据分析领域，主成分分析（Principal Component Analysis，PCA）是一种常用的数据降维技术，它能够将高维度的数据转换成低...同时，理解和掌握主成分分析的基本概念和操作流程，对于提升数据分析能力具有重要意义。
基于SPSS实现的主成分分析实例 内含主成分分析实际例子 共19页PPT.ppt
07-25
以城镇居民消费支出资料为例,用主成分分析法对各省、市作综合评价（spssex-2/城镇居民消费支出的主成分分析 ） 以经济效益数据为例，用主成分分析法对各企业作综合评价（ spssex-2/企业经济效益的主成分分析） （一...
主成分分析在SPSS中的操作详细步骤
05-10
主成分分析在 SPSS 中的操作详细步骤 在本文中，我们将详细介绍如何使用 SPSS 软件进行主成分分析，包括数据准备、数据标准化、主成分提取、主成分载荷矩阵计算、特征向量计算、主成分表达式计算、主成分综合模型...
主成分分析法及其在SPSS中的操作
08-08
主成分分析法 SPSS
【统计学笔记】方差分析表和回归分析表的解读
MYMarcoreus的博客
12-30 4万+
1. 方差分析表 1.1 单因素方差分析表 误差来源 平方和SSSSSS 自由度dfdfdf 均方MSMSMS FFF值 PPP值 FFF临界值Significance  FSignificance \; FSignificanceF 组间（因素影响）factor  Afactor \; \bold AfactorA SSASSASSA n−1n-1n−1 MSA=SSAn−1MSA = \frac{SSA}{n-1}MSA=n−1SSA​ MSAMSE\frac{MSA}{MSE}MSEM
基于spss对因子分析中总方差解释与碎石图中的冲突
m0_64857566的博客
08-01 1067
当第一个主成分解释了数据中很大一部分的方差时（例如你提供的情况下达到了76.6%），在碎石图中，你会看到从第一个主成分开始，方差解释的增长逐渐变缓，直到出现拐点。综上所述，总方差解释的特征值中第一个成分能够解释较大部分的方差，导致拐点在碎石图中出现在第二个主成分，因为从第二个主成分开始，方差解释的增长逐渐变缓。我们发现总方差解释中，第一个主成分就可以解释很大部分大部分数据方差，而碎石图中上拐点出现在第二个主成分，这就引起了冲突，这就引起了我们的思考，到底是使用第一个总方差解释的数据还是使用碎石图中的数据。
计量地理学 实验(SPSS27)
m0_53156691的博客
03-12 7674
使用SPSS（27版本）以及ArcGIS软件做的一些计量地理学实验步骤记录与简略分析。主要有如下一些实验：地理数据的统计处理、相关分析、主成分分析、多元线性回归分析、聚类分析、时间序列数据分析、因子分析、地统计分析、趋势面分析、马尔可夫分析。
SPSS主成分分析（PCA）
weixin_42191203的博客
04-01 1万+
1、导入数据 点击“文件”-“打开”-“数据”，选择要分析的数据文件“DATA.xlsx”。         2、进行主成分分析 点击“分析”-“降维”-“因子”，按下图提示进行相关操作。               3、运行结果            由“总方差解释”可知，特征根λ1=2.
主成分分析
m0_52124992的博客
01-24 5731
主成分分析
数学建模 因子分析
xht2403267701的博客
08-16 1万+
因子分析和主成分分析法是一种对数据进行降维处理的方法，但主成分分析法的弊端在于其通过计算出相关系数矩阵的特征值，进而提取出来的主成分变量通常难以被解释。而因子分析方法则解决了这一问题，其构造出的因子具有明确的物理意义因子分析是主成分分析的一种推广。............
主成分分析（Principal components analysis）-最大方差解释
qq_40259429的博客
10-24 317
https://www.cnblogs.com/jerrylead/archive/2011/04/18/2020209.html 很详细
spss主成分分析法
08-12
SPSS主成分分析法是一种常用的数据降维方法，它基于原始变量的线性组合构建主成分，并通过计算特征值和特征向量来确定主成分的数量。主成分分析的目的是在保持数据信息损失较小的前提下，将多个相关指标转化为几个互补相关的综合指标。在SPSS中，主成分分析通过计算协方差矩阵和特征值分解来实现。 具体步骤如下： 1. 计算协方差矩阵：根据原始数据计算出变量之间的协方差矩阵。 2. 求特征值和特征向量：对协方差矩阵进行特征值分解，得到特征值和对应的特征向量。 3. 选择主成分：根据特征值的大小选择主成分的数量。通常选择特征值大于1的主成分，因为这些主成分能够解释原始变量的方差的比例较高。 4. 计算主成分载荷：计算原始变量在每个主成分上的权重，也称为主成分载荷。 5. 解释主成分：根据主成分的载荷和特征值，解释每个主成分所代表的含义和贡献。 6. 解释累计贡献率：计算每个主成分的方差贡献率和累计贡献率，以确定选择的主成分数量是否足够反映原始变量的信息。 总之，SPSS主成分分析法通过将多个相关指标转化为少数几个主成分来简化数据分析，提供更方便的数据解释和可视化。<span class="em">1</span><span class="em">2</span><span class="em">3</span> #### 引用[.reference_title] - *1* *2* [spss分析方法-主成分分析](https://blog.csdn.net/Laoacai/article/details/125338365)[target="_blank" data-report-click={"spm":"1018.2226.3001.9630","extra":{"utm_source":"vip_chatgpt_common_search_pc_result","utm_medium":"distribute.pc_search_result.none-task-cask-2~all~insert_cask~default-1-null.142^v92^chatsearchT3_1"}}] [.reference_item style="max-width: 50%"] - *3* [主成分分析——SPSS实操](https://blog.csdn.net/weixin_62490408/article/details/125805919)[target="_blank" data-report-click={"spm":"1018.2226.3001.9630","extra":{"utm_source":"vip_chatgpt_common_search_pc_result","utm_medium":"distribute.pc_search_result.none-task-cask-2~all~insert_cask~default-1-null.142^v92^chatsearchT3_1"}}] [.reference_item style="max-width: 50%"] [ .reference_list ]

“相关推荐”对你有帮助么？

  • 非常没帮助
  • 没帮助
  • 一般
  • 有帮助
  • 非常有帮助
提交
评论 1
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值