线索化 - 遍历思想，流程，代码

1、前言

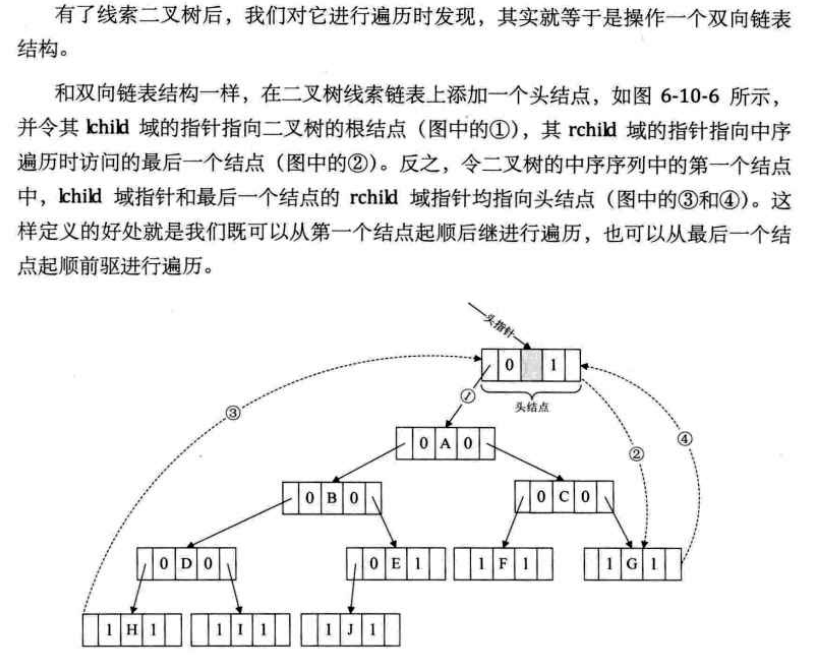
普通二叉树只能找到结点的左右孩子信息，而该结点的直接前驱和直接后继只能在遍历过程中获得。

若可将遍历后对应的有关前驱和后继预存起来，则从第一个结点开始就能很快“顺藤摸瓜”而遍历整个树了。

二叉线索树思想是干什么的？

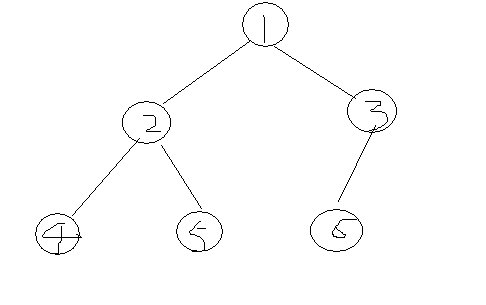
中序遍历这棵树===》转换成链表访问

2线索化思想

结论：线索化过程就是在遍历过程（假设是中序遍历）中修改空指针的过程：

将空的lchild改为结点的直接前驱；

将空的rchild改为结点的直接后继。

3线索化思想

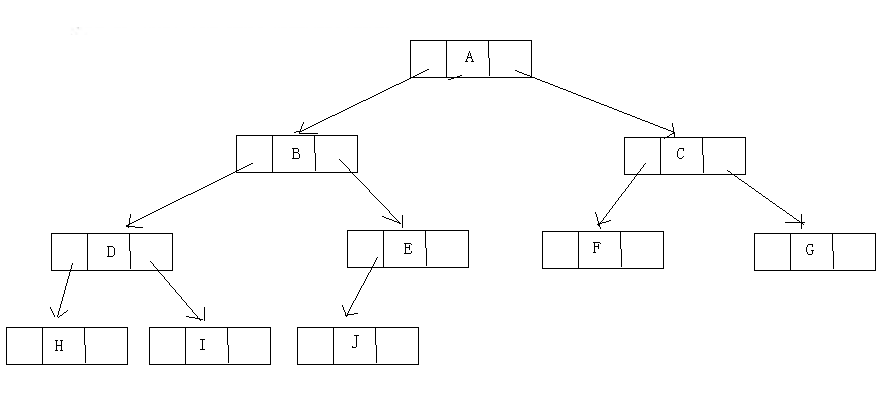
请将此树线索化。

1）右空指针线索化：

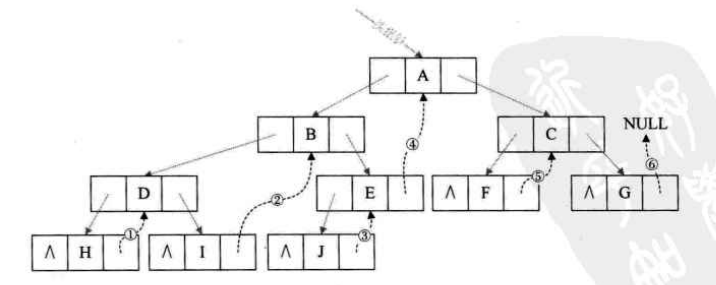
2）左空指针线索化

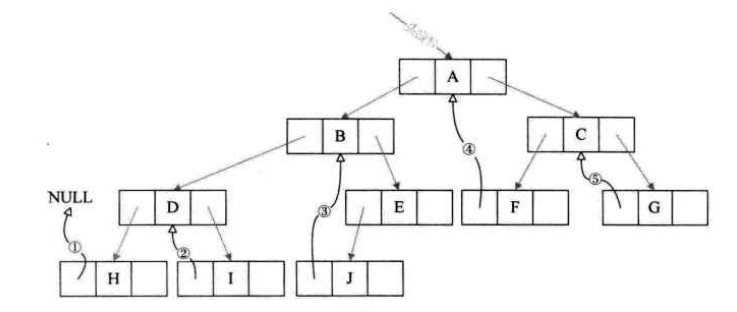
3）总结

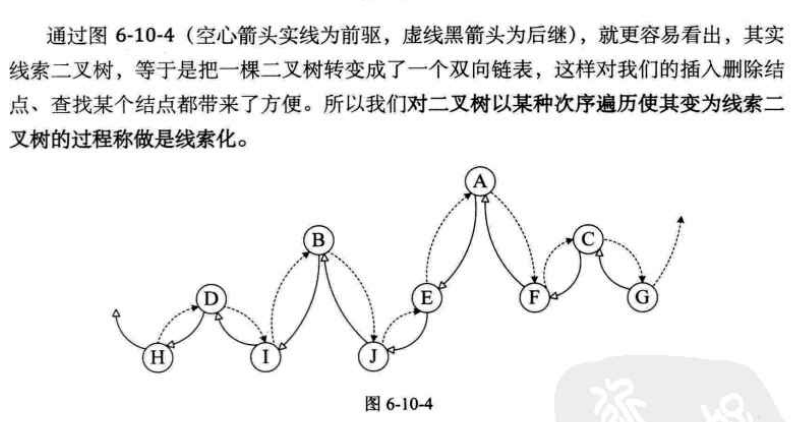
线索化的本质：让前后结点，建立关系；

1）两个辅助指针变量形成差值后：后继结点的左孩子指向前驱结点，前驱结点的右孩子指向后继结点。

2）赋值指针变量和业务操作的逻辑关系

代码：

// threadTree.cpp
// 树的线索化

#define _CRT_SECURE_NO_WARNINGS
#include <iostream>
#include <cstdio>
#include <stack>

using namespace std;

// Link == 0表示指向左右孩子指针
// Thread==1表示指向前驱或者后继的线索
#define Thread 1
#define Link 0

// 二叉线索存储结点结构
typedef struct BiThrNode
{
	char data;
	struct BiThrNode *lchild, *rchild;
	int LTag;
	int RTag; // 左右标志
}BiThrNode, *BiThrTree;

char Nil = '#'; // 字符型以空格符为空

// 按前序输入二叉线索树中结点的值，构造二叉线索树T
BiThrNode* createBiThrTree()
{
	BiThrNode *tmp = NULL;
	char ch;
	scanf("%c", &ch);
	
	if (ch == '#') {
		return NULL;
	}
	else {
		tmp = (BiThrNode *)malloc(sizeof(BiThrNode));
		if (tmp == NULL) {
			return NULL;
		}
		memset(tmp, 0, sizeof(BiThrNode));
		tmp->data = ch;
		tmp->lchild = createBiThrTree(); // 递归构造左子树
		tmp->rchild = createBiThrTree();
	}
	return tmp;
}

BiThrNode *pre; // 全局变量，始终指向刚刚访问过的结点

// 中序遍历进行中序线索化
void inThreading(BiThrNode *p)
{
	if (p) {
		inThreading(p->lchild); // 递归左子树线索化
		if (!p->lchild) { // 没有左子树
			p->LTag = Thread; // 前驱线索
			p->lchild = pre;// 左孩子指向前驱
		}
		if (!pre->rchild) { // 前驱没有又孩子
			pre->RTag = Thread; // 后继线索
			pre->rchild = p; // 前驱又孩子指向后继
		}
		pre = p; // 保持pre指向p的前驱
		inThreading(p->rchild); // 递归右子树线索化
	}
}

// 中序遍历二叉树T，并将其中序线索化，thrt指向头结点
BiThrNode* inOrderThreading(BiThrTree T)
{
	BiThrNode *Thrt = NULL;

	Thrt = (BiThrNode *)malloc(sizeof(BiThrNode));
	if (!Thrt) {
		return NULL;
	}
	memset(Thrt, 0, sizeof(BiThrNode));

	Thrt->LTag = Link; // 左孩子为孩子指针
	Thrt->RTag = Thread; // 右孩子为线索化的指针
	Thrt->rchild = Thrt; // 右指针回指
	if (!T) { // 若二叉树为空，则左指针回指
		Thrt->lchild = Thrt;
	}
	else {
		Thrt->lchild = T; // 步骤1
		pre = Thrt;
		inThreading(T); // 中序遍历进行中序线索化
		pre->rchild = Thrt;// 步骤4
		pre->RTag = Thread; // 最后一个结点线索化
		Thrt->rchild = pre; // 步骤2
	}
	return Thrt;
}

/* 中序遍历二叉线索树T(头结点)的非递归算法 */
int InOrderTraverse_Thr(BiThrNode* T)
{
	BiThrNode* p;
	p = T->lchild; /* p指向根结点 */
	while (p != T)
	{
		/* 空树或遍历结束时,p==T */
		while (p->LTag == Link)
			p = p->lchild;
		printf("%c ", p->data);

		//如果中序遍历的最后一个结点的 右孩子 == T 说明到最后一个结点 ,遍历结束..
		while (p->RTag == Thread && p->rchild != T)
		{
			p = p->rchild;
			printf("%c ", p->data);
		}
		p = p->rchild;
	}
	return 0;
}

/* 中序遍历二叉线索树T(头结点)的非递归算法 */
int InOrderTraverse_Thr2(BiThrNode* T)
{
	BiThrNode* p;
	p = T->rchild; /* p指向根结点 */
	while (p != T)
	{
		/* 空树或遍历结束时,p==T */
		while (p->RTag == Link)
			p = p->rchild;
		printf("%c ", p->data);

		//如果中序遍历的最后一个结点的 右孩子 == T 说明到最后一个结点 ,遍历结束..
		while (p->LTag == Thread && p->lchild != T)
		{
			p = p->lchild;
			printf("%c ", p->data);
		}
		p = p->lchild;
	}
	return 0;
}


void operatorTree()
{
	BiThrTree T, H;
	printf("请按前序输入二叉树(如:'ABDH##I##EJ###CF##G##')\n");
	T = createBiThrTree(); // 按前序产生二叉树 
	H = inOrderThreading(T); // 中序遍历,并中序线索化二叉树 
	printf("中序遍历(输出)二叉线索树:\n");
	InOrderTraverse_Thr(H); // 中序遍历(输出)二叉线索树 
	// H D I B J E A F C G

	printf("\n逆序访问:");
	InOrderTraverse_Thr2(H);
	// G C F A E J B I D H

	printf("\n");
}

int main()
{
	operatorTree();

	return 0;
}