蓝桥杯训练1——贪心算法——地形盛水

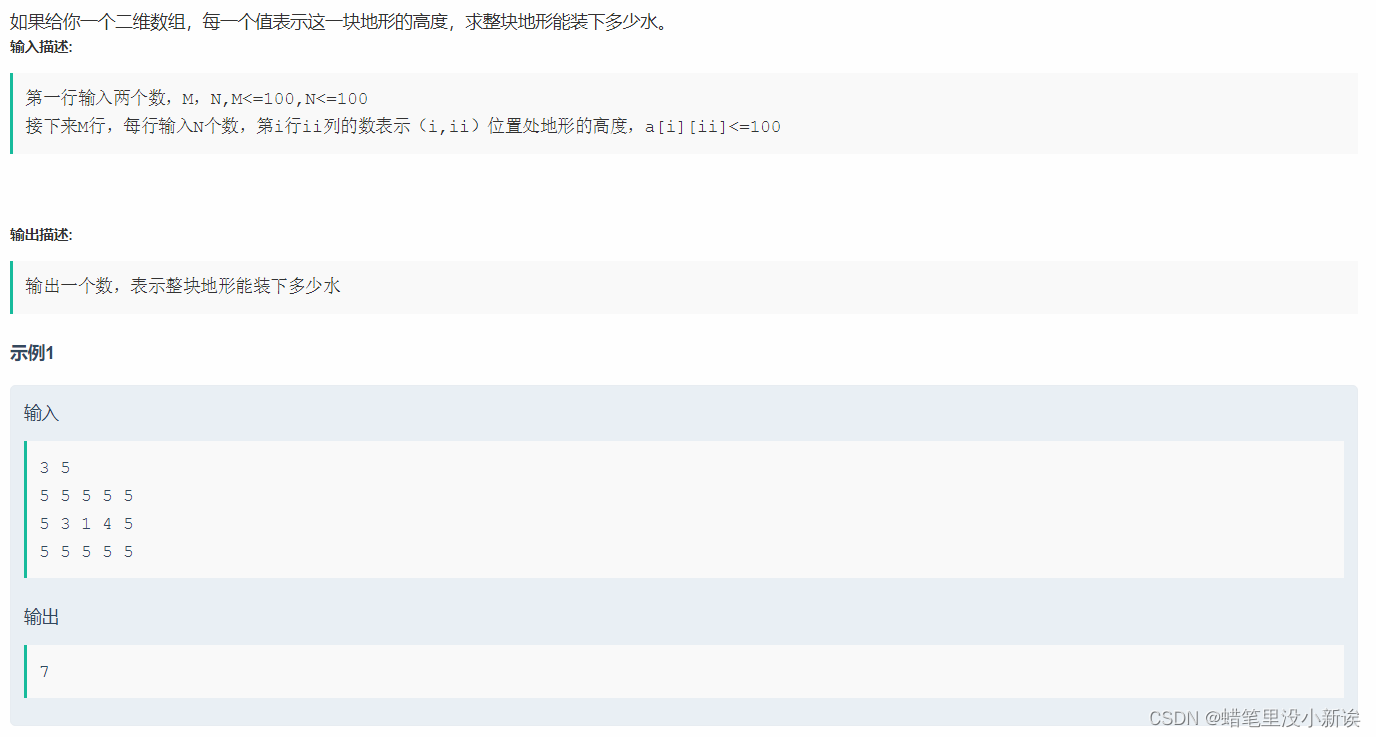
地形盛水（题目来自牛客网）

思路解读

设置变量：
bf 字符流缓冲区
n，m 矩阵的行和列
heightMap 水位二维数组
Node 每一个方框
Node.row 方框的行号
Node.col 方框的列号
Node.value 方框的水位值
ans 输出结果
max 当前水位的阀值
N，M 同 n，m
isEnter 标识是否已经进过堆的二维boolean型数组
heap 小根堆

设置小根堆，小根堆按照水位高度从小排到大，小根堆实际上就是优先级队列PriorityQueue，按照从小到大进行排列，先将整个边框进堆，即最外层的数据先进队列，然后从中挑选最小的的方格，该方格为当前的阀值，即最低点，初始设置一个最大值max，若当前挑选出来的方格的水位比最大值max高，则更新max的值为当前挑选出来的方框的水位值，然后将max与当前方框的上下左右放款进行比较，若比当前max的值小，则计算水位差，加入最终结果ans，将该方框进堆，且标志该方框为已经进过堆，即isEnter = true，若比当前max的值大，则直接进堆，并修改该方框的isEnter = true，表示已经进过堆。若堆不为空，则继续寻找最小方框，反复，直到堆为空。

AC代码

import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.util.Comparator;
import java.util.PriorityQueue;

public class Main {
	static BufferedReader bf = new BufferedReader(new InputStreamReader(System.in));

	public static void main(String[] args) throws Exception{
		String [] s = bf.readLine().split(" ");
		int n = Integer.parseInt(s[0]);
		int m = Integer.parseInt(s[1]);
		int [][] heightMap = new int[n][m];
		for(int i=0;i<n;i++) {
			s = bf.readLine().split(" ");
			for(int j=0;j<m;j++) {
				heightMap[i][j] = Integer.parseInt(s[j]);
			}
		}
		System.out.println(Main.trapRainWater(heightMap));
	}

	public static class Node {
		public int value;
		public int row;
		public int col;

		public Node(int row, int col, int value) {
			this.row = row;
			this.col = col;
			this.value = value;
		}
	}

	public static int trapRainWater(int [][] heightMap) {
		int ans = 0;
		int max = 0;
		if(heightMap == null || heightMap.length == 0 || heightMap[0] == null || heightMap[0].length == 0) {
			return 0;
		}
		int N = heightMap.length;
		int M = heightMap[0].length;
		
		boolean [][] isEnter = new boolean[N][M];
//		优先级队列就是一个小根堆
		PriorityQueue<Node> heap = new PriorityQueue<Node>(new NodeComparator()); 
		
		for(int col = 0; col < M - 1; col++) {
			isEnter[0][col] = true;
			heap.add(new Node(0,col,heightMap[0][col]));
		}
		for(int row = 0; row < N - 1; row++) {
			isEnter[row][M-1] = true;
			heap.add(new Node(row,M-1,heightMap[row][M-1]));
		}
		for(int col = M - 1; col > 0; col--) {
			isEnter[N-1][col] = true;
			heap.add(new Node(N-1,col,heightMap[N-1][col]));
		}
		for(int row = N - 1; row > 0; row--) {
			isEnter[row][0] = true;
			heap.add(new Node(row,0,heightMap[row][0]));
		}
		
		while(!heap.isEmpty()) {
			Node node = heap.poll();
			int value = node.value;
			int row = node.row;
			int col = node.col;
			if (value > max)
				max = value;
			if(row - 1 >= 0 && !isEnter[row - 1][col]) {
				isEnter[row - 1][col] = true;
				if(heightMap[row - 1][col] < max) {
					ans += max - heightMap[row - 1][col];
				}
				heap.add(new Node(row - 1, col, heightMap[row - 1][col]));
			}
			if(col - 1 >= 0 && !isEnter[row][col - 1]) {
				isEnter[row][col - 1] = true;
				if(heightMap[row][col - 1] < max) {
					ans += max - heightMap[row][col - 1];
				}
				heap.add(new Node(row, col - 1, heightMap[row][col - 1]));
			}
			if(row + 1 < N && !isEnter[row + 1][col]) {
				isEnter[row + 1][col] = true;
				if(heightMap[row + 1][col] < max) {
					ans += max - heightMap[row + 1][col];
				}
				heap.add(new Node(row + 1, col, heightMap[row + 1][col]));
			}
			if(col + 1 < M && !isEnter[row][col + 1]) {
				isEnter[row][col + 1] = true;
				if(heightMap[row][col + 1] < max) {
					ans += max - heightMap[row][col + 1];
				}
				heap.add(new Node(row, col + 1, heightMap[row][col + 1]));
			}
		}
		return ans;
	}

	public static class NodeComparator implements Comparator<Node> {

		@Override
		public int compare(Node o1, Node o2) {

			return o1.value - o2.value;
		}

	}
}