MLAPP 读书笔记 - 05-1 贝叶斯统计(Bayesian statistics)

MLAPP 读书笔记 - 05 贝叶斯统计(Bayesian statistics)

A Chinese Notes of MLAPP，MLAPP 中文笔记项目
https://zhuanlan.zhihu.com/python-kivy

转载：cycleuser

侵权立删，本意是为广大学习爱好者提供中文资料，同时在这里补充了图片，方便阅读，如果有任何法律问题，我会立即删除。

5.1 概论

之前咱们已经看到过很多不同类型的概率模型了,然后也讲了如何用这些模型拟合数据,比如讲到了如何去进行最大后验估计(MAP)参数$\hat{\theta }=\arg \max p(\theta |D)$,使用各种不同先验等等.还讲了全后验(full posterior)$p(\theta |D)$,以及一些特定情境下的后验预测密度(posterior predictive density)$p(x|D)$(后面的章节中会介绍更多通用算法).

对未知变量,使用后验分布来总结我们知道的信息,这就是贝叶斯统计学的核心思想.在本章要对这个统计学上的方法进行更详细讲解,在本书第六章,也就是下一章,会讲解另一种统计方法,也就是频率论统计,或者也叫做经典统计(frequentist or classical statistics).

5.2 总结后验分布

后验分布$p(\theta |D)$总结了我们关于未知量$\theta$的全部信息.在本节我们会讨论一些从一个概率分布,比如后验等,能推出来的简单量.这些总结性质的统计量通常都比全面的联合分布(full joint)更好理解也更容易可视化.

5.2.1 最大后验估计(MAP estimation)

通过计算后验均值(mean)/中位数(median)或者众数(mode)我们可以很容易地对一个未知量进行点估计(point
estimate).在本书5.7,会讲到如何使用决策理论(decision theory)在这些不同方法之间进行选择.通常后验均值或者中位数最适合用于对实数值变量的估计,而后验边缘分布(posterior marginals)的向量最适合对离散向量进行估计.不过后验模,也就是最大后验估计(MAP estimate)是最流行的,因为这将问题降低到了一个优化问题(optimization problem),这样就经常能有很多高效率的算法.另外,最大后验分布还可以用非贝叶斯方式(non-Bayesian terms)来阐述,将对数先验(log prior)看作是正则化工具(regularizer)(更多内容参考本书6.5).

虽然最大后验估计的方法在计算上很有吸引力,但还是有很多缺陷的,下面就要详细讲一讲.这也为对贝叶斯方法的详尽理解提供了动力,本章后文以及本书其他地方会讲到.

此处参考原书图5.1

5.2.1.1 无法测量不确定度

最大后验估计(MAP estimation)最明显的一个缺陷就在于没有对不确定性提供任何量度,其他的各种点估计比如后验均值或者中位数也都有这个问题.在很多应用中,都需要知道对一个估计值到底能信任多少.对于后验置信度的度量可以推导出来,在本书5.2.2中有.

5.2.1.2 可能导致过拟合

最大后验分布估计中进行插值可能导致过拟合.在机器学习里面,对于预测准确性往往比模型参数的可解释性更看重.不过如果对参数的不确定度不能建模的话,就可能会导致预测分布过分有信心(overconfident).在本书第三章有若干这类例子,后面还会看到更多.在风险敏感的情况下,对预测过分置信就可能很是个问题了,具体参考本书5.7.

5.2.1.3 众数(mode)是非典型点(untypical point)

选择众数(mode)来作为一个后验分布的总结通常是非常差的选择,因为众数在一个分布通常不典型的,而不像均值或者中位数那样有代表意义.这一点如图5.1(a)所示,图中是一个一维连续空间.最基本的问题是众数是在测量值为0的位置的一个点,而均值和中位数都把空间的体积(volume)考虑了进去.另外一个例子如图5.1(b)所示:这里面的众数是0,但均值则是非零的.对方差之类的参数进行推测的时候就很容易遇到这种特别完犊子的分布形态,尤其是在分层模型(hierarchical models)中.这种情况下最大后验估计(MAP)和最大似然估计(MLE)很明显都是很差的估计.

如果众数不是一个好的选择,那该怎么去对一个后验分布进行总结概括呢?答案就是使用决策理论(decision theory),在本书5.7会讲到.基本思想就是设置一个损失函数(loss function),其中的$L(\theta ,\hat{\theta })$表示的意思是在真实值是$\theta$而你估计值是$\hat{\theta }$的时候造成的损失(loss).如果使用0-1二值化量化损失,即$L(\theta ,\hat{\theta })=I(\theta \ne \hat{\theta })$,那么最优估计就是后验众数了.0-1损失函数就意味着你只使用那些没有误差的点,其他有误差的就不要了:这样这种损失函数的情况下就没有部分置信(partial credit)了.对于连续值变量,通常用平方误差损失函数$L(\theta ,\hat{\theta })=(\theta -\hat{\theta }{)}^2$;对应的最优估计就是后验均值,这也会在本书5.7讲到.或者也可以使用一个更健壮的损失函数,也就是绝对值损失函数:$L(\theta ,\hat{\theta })=|\theta -\hat{\theta }|$,这时候最佳估计就是后验中位数了.

此处参考原书图5.2

5.2.1.4 最大后验估计(MAP estimation)对重参数化(reparameterization)是可变的(not invariant)*

最大后验估计(MAP estimation)的一个更严重问题就是得到的结果依赖于如何对概率分布进行参数化.从一种参数形式转换到另一种等价的参数形式,就会改变结果,这很显然略坑,因为测量单位可以是任意的(比如说测量距离的时候用的单位可以使厘米或者英寸).

为了便于理解,假设要计算x的后验分布.如果定义$y=f(x)$,可以根据等式2.87得到y的分布,这里重复一下:
$p_y(y)=p_x(x)|\frac{dx}{dy}|$(5.1)

上面的$|\frac{dx}{dy}|$叫做雅可比项(Jacobian),衡量的是经过函数f之后单位体积的变化规模.设$\hat{x}=\arg {\max }_x{p}_x(x)$是对x的最大后验估计(MAP estimation).通常来说这并不意味着通过函数$f(\hat{x})$就能得到$\hat{y}=\arg {\max }_y{p}_y(y)$.例如,设$x\sim N(6,1),y=f(x)$,其中有:
$f(x)=\frac{1}{1+\exp (-x+5)}$(5.2)

然后使用蒙特卡罗模拟方法(Monte Carlo simulation)(参考本书2.7.1)来推导出y的分布.结果如图5.2所示.可见原来的正态分布被S型非线性函数给"压缩"了.具体来说就是变换后分布的众数和变换之前的众数是不相等的.

在最大似然估计的过程中遇到这种问题会怎么样呢?设想下面这个例子,参考资料 Michael Jordan.伯努利分布(Bernoulli distribution)通常是使用均值(mean)$\mu$来参数化的,也就是 p ( y = 1 ∣ μ ) = μ , y ∈ { 0 , 1 } p(y=1|\mu)=\mu , y\in\{0,1\} p(y=1∣μ)=μ,y∈{0,1}.假设在单位间隔(unit interval)上用一个均匀先验(uniform prior):$p_{\mu }(\mu )=1I(0\le \mu \le 1)$.如果没有数据,最大后验估计正好就是先验的众数(mode)可以在0和1之间的任意位置.不同的参数化就会在这个区间中选择任意的不同的点.

首先设$\theta =\sqrt{\mu },\mu ={\theta }^2$.新的先验就是:

$p_{\theta }(\theta )=p_{\mu }(\mu )|\frac{d\mu }{d\theta }|$(5.3)

对于$\theta \in [0,1]$,新的众数就是:

${\hat{\theta }}_{MAP}=\arg {\max }_{\theta \in [0,1]}2\theta =1$(5.4)

然后设$\varphi =1-\sqrt{1-\mu }$,新的先验就是:

$p_{\varphi }(\varphi )=p_{\mu }(\mu )|\frac{d\mu }{d\theta }|=2(1-\varphi )$(5.5)

对于$\varphi \in [0,1]$,新的众数就是:

$\hat\theta_{MAP} = \arg\max_{\theta\in[0,1]}2-2\phi =0 $(5.6)

所以最大后验估计明显是依赖参数化设置的.最大似然估计(MLE)就不会有这个问题,因为似然率函数是一个函数而不是概率密度.贝叶斯方法也不会有这个问题,因为测量过程的变化在对参数空间上进行积分的时候都考虑进去了.

这个问题的一个解决方案就是优化下面的目标函数(objective function):

$\hat{\theta }=\arg {\max }_{\theta }p(D|\theta )p(\theta )|I\theta {|}^{-\frac{1}{2}}$(5.7)

这里的$I(\theta )$就是与$p(x|\theta )$相关的费舍信息矩阵(Fisher information matrix)(具体参考本书6.2.2).这个估计与参数化相独立,具体原因如(Jermyn 2005; Druilhet and Marin 2007)所述.然而很悲剧,对等式5.7进行优化通常都很难,这就极大降低了这个方法的吸引力了.

5.2.2 置信区间

除点估计外,我们经常还要对置信度进行衡量.标准的置信度衡量值是某个(标量 scalar)值$\theta$,对应的是后验分布的"宽度(width)".这可以使用一个$100(1-\alpha )$置信区间(credible interval),是一个(连续(contiguous))区域$C=(l,u)$(这里的l和u的意思是lower和upper的缩写,表示的就是下界和上界),这个区域包含了$1-\alpha$的后验概率质量,即:

$C_{\alpha }(D)=(l,u):P(l\le \theta \le u|D)=1-\alpha$(5.8)

可能会有很多个这样的区间,我们要选一个能满足在每个尾部(tail)有$(1-\alpha )/2$概率质量的一个区间,这个区间就叫做中央区间(central interval).

此处参考原书图5.3

如果一个后验分布有已知的函数形式,就可以使用$l=F^{-1}(\alpha /2),u=F^{-1}(1-\alpha /2)$来计算得到后验中央区间,其中的F就是后验的累积密度函数(cdf).例如,如果后验是正态分布,$p(\theta |D)=N(0,1),\alpha =0.05$,这样就能得到了$l=\Phi (\alpha /2)=-1.96,u=\Phi (1-\alpha /2)=1.96$,其中的$\Phi$表示的是正态分布的累积密度函数(cdf).如图2.3©所示.这也证明了实际应用中使用$\mu \pm 2\sigma$做置信区间的可行性,其中的$\mu$表示的是后验均值,$\sigma$表示的是后验标准差,2是对1.96的一个近似.

当然了,后验分布也不可能总是正态分布的.比如对于抛硬币的那个例子来说,如果使用一个均匀先验,然后观察出N=100次试验中有$N_1=47$次人头朝上,那么后验分布就是一个$\beta$分布,即$p(\theta |D)=Beta(48,54)$.然后会发现其中95%的后验置信区间位于(0.3749,0.5673)(可以参考本书配套的PMTK3当中的betaCredibleInt,里面是单行MATLAB代码来进行这个计算).

如果我们不知道其函数形式,但可以从后验中进行取样,那么也可以使用蒙特卡罗方法近似来对后验的量进行估计:简单排序S个样品,然后找到其中一个出现在排序列表中的$\alpha /S$位置上的样本.由于$S\to \infty$,这就会收敛到真实值了.具体可以参考本书配套PMTK3当中的mcQuantileDemo.

人们总容易对贝叶斯方法置信区间(Bayesian credible intervals)和频率论的信心区间(frequentist confidence intervals)产生混淆.这两个可不是一回事,本书6.6.1会详细讲到.一般来说,贝叶斯的置信区间往往是人们要去计算的,而实际上他们通常计算的却都是频率论的信心区间,这是因为大多数人都是学习的频率论的统计学,而不是贝叶斯方法统计学.好在计算贝叶斯置信区间和计算频率论信心区间的方法都不太难,这部分可以参考本书配套PMTK3当中的betaCredibleInt来查看如何在MATLAB中进行计算.

5.2.2.1 最高后验密度区(Highest posterior density regions)*

此处参考原书图5.4

中央区间的一个问题在于可能有不在这个区间内的点却有更高的概率密度,这如图5.3(a)所示,其中左侧置信区间边界之外的点就比右侧区间外的点有更高的概率.

这也导致了另外一个有用的变量,即最高后验密度(highest posterior density,缩写为HPD)区域.这个可以定义为组成总体概率质量的$100(1-\alpha )\%$最可能的点(的集合).更正式来说,可以定义概率密度函数(pdf)上的阈值(threshold)$p^{\ast }$,满足:

$1-\alpha ={\int }_{\theta :p(\theta |D)>p^{\ast }}p(\theta |D)d\theta$(5.9)

然后就可以定义最高后验密度区(HPD)为:
C α ( D ) = { θ : p ( θ ∣ D ) > p ∗ } C_\alpha(D)=\{\theta:p(\theta|D)>p^*\} Cα​(D)={θ:p(θ∣D)>p∗}(5.10)

在一维情况下,最高后验密度区(HPD)也叫做最高密度区间(highest density interval,缩写为HDI).例如图5.3(b)所示就是一个$Beta(3,9)$分布的95%的最高密度区间(HDI),也就是(0.04,0.48).可以发现这要比置信区间(CI)要更窄一些,虽然也是包含了95%的概率质量;另外,这个区间内的每个点都比区间外的点有更高的概率.

对一个单峰分布(unimodal distribution)来说,最高密度区间(HDI)是围绕众数包含95%概率质量的最窄区间了.可以想象一些灌水的逆过程,将水平面逐渐降低,直到95%的质量暴露出来,而只有5%的部分被淹没.这就使得在一维情况下对最高密度区间(HDI)的计算有了一个很简单的算法:搜索每个点,使区间包含95%的概率质量,然后又有最小的宽度.这可以通过一维数值优化来实现,只要知道概率分布累积密度函数(cdf)的逆函数就可以了,或者如果有一部分样本的话,可以在排序过的数据点上进行搜索(具体可以参考PMTK3当中的betaHPD).

如果后验分布是多峰(multimodal)分布,那么最高密度区间(HDI)可能就不是单个连续区间了,如图5.4(b)所示.不过对多峰后验分布进行总结通常都挺难的.

5.2.3 比例差别的推导(Inference for a difference in proportions)

有时候有很多个参数,然后要计算这些参数的某些函数的后验分布.例如,假设你要从亚马逊买个东西,然后有两个不同的卖家,提供同样的价格.第一个卖家有90个好评,10个差评,第二个卖家有2个好评没有差评,那你从哪个卖家那里买呢?

此处查看原书图5.5

刚一看,好像你应该选第二个卖家,但也不见得很有信心,因为第二个卖家的评价太少了.本章咱们就用贝叶斯分析(Bayesian analysis)来处理一下这个问题.类似的方法还可以用于其他背景下的不同群体之间的比率或比值的对比.

设${\theta }_1,{\theta }_2$分别是两个卖家的可信度,都是未知的.没有啥其他信息,就都用均匀先验${\theta }_i\sim Beta(1,1)$.这样后验分布就是$p({\theta }_1|D_1)=Beta(91,11),p({\theta }_2|D_2)=Beta(3,1)$.
咱们要计算的是$p({\theta }_1>{\theta }_2|D)$.为了方便起见,这里定义一个比率的差值$\delta ={\theta }_1-{\theta }_2$.(或者也可以用对数比(log-odds ratio)).使用下面的数值积分就可以计算目标变量:

$p(\delta >0|D)={\int }_0^1{\int }_0^{1}I({\theta }_1>{\theta }_2)Beta({\theta }_1|y_1+1,N_1-y_1+1)Beta({\theta }_2|y_2+1,N_2-y_2+1)d{\theta }_{1}d{\theta }_2$(5.11)

经过计算会发现$p(\delta >0|D)=0.710$,也就意味着最好还是从第一个卖家那里买!具体可以参考本书配套的PMTK3中的amazonSellerDemo查看代码.(这个积分也可以以解析形式解出来(Cook 2005).)

解决这个问题有一个更简单的方法,就是使用蒙特卡洛方法抽样来估计后验分布$p(\delta |D)$.这就容易多了,因为在后验中${\theta }_1,{\theta }_2$两者是相互独立的,而且都遵循$\beta$分布,可以使用标准方法进行取样.分布$p({\theta }_i|D_i)$如图5.5(a)所示,而对$p(\delta |D)$的蒙特卡罗方法(MC)估计,总共95%的最高后验密度(HPD)区域如图5.5(b)所示.对$p(\delta >0|D)$的蒙特卡罗方法估计是通过计算样本中${\theta }_1>{\theta }_2$的部分,这样得到的值是0.718,和真实值已经非常接近了.(具体可以参考本书配套的PMTK3中的amazonSellerDemo查看代码.)

5.3 贝叶斯模型选择

在图1.18中,我们看到了使用过高次多项式拟合导致了过拟合,而用过低次数多项式又导致了欠拟合.类似的,在图7.8(a)中可以看到使用的归一化参数(regularization parameter)太小会导致过拟合,而太大又导致欠拟合.一般来说,面对着一系列不同复杂性的模型(比如不同的参数分布族)可选的时候,咱们该怎么选择呢?这就是所谓的模选择问题(model selection problem).

一种方法是使用交叉验证(cross-validation),估算所有备选模型的泛化误差(generalization error),然后选择最优模型.不过这需要对每个模型拟合K次,K是交叉验证的折数(CV folds).更有效率的方法是计算不同模型的后验:

$p(m|D)=\frac{p(D|m)p(m)}{{\sum }_{m\in M}}p(m,D)$(5.12)

然后就很容易计算出最大后验估计模型(MAP model),$\hat{m}=\arg \max p(m|D)$,这就叫做贝叶斯模型选择(Bayesian model selection).

如果对模型使用均匀先验,即$p(m)\propto 1$,这相当于挑选能够让下面的项目最大化的模型:

$p(D|m)=\int p(D|\theta )p(\theta |m)d\theta$(5.13)

这个量也叫做模型m的边缘似然率(marginal likelihood),积分似然率(integrated likelihood)或者证据(evidence).具体如何进行积分在本书5.3.2有讲解.不过首先来对这个量的含义给出一下直观解释.

5.3.1 贝叶斯估计的奥卡姆剃刀

有人可能会觉得使用$p(D|m)$来选择模型可能总会偏向于选择有最多参数的模型.如果用$p(D|{\hat{\theta }}_m)$来选择模型,那么确实如此,其中的${\hat{\theta }}_m$是模型m的参数的最大似然估计(MLE)或者最大后验估计(MAP),因为有更多参数的模型会对数据有更好的拟合,因此就能得到更高的似然率(higher likelihood).不过如果对参数进行积分,而不是最大化,就能自动避免过拟合了:有更多参数并不必然就有更高的边缘似然率(marginal likelihood).这就叫做贝叶斯奥卡姆剃刀效应(Bayesian Occam’s razor effect, MacKay 1995b; Murray and Ghahramani 2005),这是根据奥卡姆剃刀原则得名的,其要旨是说应该选择能解释数据的最简单模型.

理解贝叶斯奥卡姆剃刀的一种方式是将边缘似然率改写成下面的形式,基于概率论的链式规则(等式2.5):
$p(D)=p(y_1)p(y_2|y_1)p(y_3|y_{1:2})...p(y_N|y_{1:N-1})$(5.14)

上式中为了简单起见去掉了关于x的条件.这个和留一交叉验证法(leave-one-out cross-validation)估计似然率(likelihood)(本书1.4.8)看着很相似,因为也是给出了之前的全部点之后预测未来的每个点的位置.(当然了,上面表达式中,数据的顺序就没有影响了.)如果一个模型太复杂,在早期样本的时候就可能会过拟合,对后面余下的样本的预测也可能很差.

此处查看原书图5.6

另外一种理解贝叶斯奥卡姆剃刀效应的思路是参考概率总和积累起来必然是1.这样就有${\sum }_{D^{\prime }}p(D^{\prime }|m)=1$,其中的求和是在全部可能的数据点集合上进行的.复杂的模型可能进行很多预测,就必须把概率质量分散得特别细(thinkly),然后对任意给定数据就不能得到简单模型一样大的概率.这也叫做概率质量守恒原则(conservation of probability mass principle),如图5.6所示.水平方向的是所有可能的数据集,按照复杂性递增排序(以某种抽象概念来衡量).在纵轴上投下的是三个可能的概率模型:$M_1,M_2,M_3$复杂性递增.实际观测到底数据为竖直线条所示的$D_0$.图示可知,第一个模型太简单了,给$D_0$的概率太低.第三个模型给$D_0$的概率也很低,因为分布的更宽更窄.第二个模型就看上去正好,给已经观测到底数据给出了合理的置信程度,但又没有预测更多.因此第二个模型是最可选的模型.

图5.7中的数据也是贝叶斯奥卡姆剃刀的一个样例.其中的多项式次数分别为1,2,3,对于N=5个数据点.另外还展示了各个模型的后验,其中使用了正态分布先验(更多细节参考本书7.6).由于没有足够的数据,不能判断复杂模型,所以最大后验估计模型(MAP model)就是d=1.图5.8展示的是当样本规模扩大到N=30的时候的情况.这时候就很明显了d=2是最佳模型(实际上这时候的数据就是用一个二次函数生成的).

另一个例子是图7.8©,其中是对数投图的$\log p(D|\lambda )$和$\log (\lambda )$,对应的是多项式岭回归模型(polynomial ridge regression model),其中的$\lambda$和交叉验证试验中用的值有相同的范围.可见最大证据(maximum evidence)大概就出现在测试的均方误差(MSE)最小的时候,也就是对应着交叉验证所选择的点.

当使用贝叶斯方法的时候,我们不仅可以仅对有限数值网格来计算证据(evidence).可以用数值优化来找到${\lambda }^{\ast }=\arg {\max }_{\lambda }p(D|\lambda )$.这个方法也叫做经验贝叶斯(empirical Bayes)或者二类最大似然估计(type II maximum likelihood)(参考本书5.6).样例可以参考本书图7.8(b):可以看到曲线和交叉验证估计的形状相似,但计算效率要更高.

此处查看原书图5.7

5.3.2 计算边缘似然率(证据)

当我们讨论推导一个混合模型的参数的时候,通常会写:
$p(\theta |D,m)\propto p(\theta |m)p(D|\theta ,m)$(5.15)

然后忽略掉归一化常数$p(D|m)$.因为$p(D|m)$相对于$\theta$来说是恒定的,所以这样也有效.不过如果对比模型的话,需要知道如何去计算边缘似然率(marginal likelihood)$p(D|m)$.一般来说这就挺麻烦,因为必须要对所有可能的参数值来进行积分,但是如果有了一个共轭先验,就很容易计算了.

设$p(\theta )=q(\theta )/Z_0$是先验,然后$q(\theta )$是一个未归一化的分布(unnormalized distribution),而$Z_0$是针对这个先验的归一化常数.设$p(D|\theta )=q(D|\theta )/Z_l$是似然率(likelihood),其中的$Z_l$包含了似然函数中的任意常数项.最终设$p(\theta |D)=q(\theta |D)/Z_N$是后验,其中的$q(\theta |D)=q(D|\theta )q(\theta )$是未归一化的后验,而$Z_N$是这个后验的归一化常数.则有:
$$\begin{array}{rlr}p(\theta |D)& =\frac{p(D|\theta )p(\theta )}{p(D)}& \text{(5.16)}\\ \frac{q(\theta |D)}{Z_N}& =\frac{q(D|\theta )q(\theta )}{Z_l{Z}_{0}p(D)}& \text{(5.17)}\\ p(D)& =\frac{Z_N}{Z_0{Z}_l}& \text{(5.18)}\end{array}$$

所以只要归一化常数能算出来,就可以很简单地计算出边缘似然率了.接下来会给出一些例子.

此处查看原书图5.8

5.3.2.1 $\beta$-二项模型(Beta-binomial model)

先把上面的结论用到$\beta$-二项模型上面.已知了$p(\theta |D)=Beta(\theta |a^{\prime },b^{\prime }),a^{\prime }=a+N_1,b^{\prime }=b+N_0$.这个后验的归一化常数是$B(a^{\prime },b^{\prime })$.因此有:

$$\begin{array}{rlr}p(\theta |D)& =\frac{p(D|\theta )p(\theta )}{p(D)}& \text{(5.19)}\\ & =\frac{1}{p(D)}[\frac{1}{B(a,b)}{\theta }^{a-1}(1-\theta {)}^{b-1}][\left(\genfrac{}{}{0ex}{}{N}{N-1}\right){\theta }^{N_1}(1-\theta {)}^{N_0}]& \text{(5.20)}\\ & =\left(\genfrac{}{}{0ex}{}{N}{N-1}\right)\frac{1}{p(D)}\frac{1}{B(a,b)}[{\theta }^{a+N_1-1}(1-\theta {)}^{b+N_0-1}]& \text{(5.21)}\end{array}$$

因此有:

$$\begin{array}{rlr}\frac{1}{B(a+N_1,b+N_0)}& =\left(\genfrac{}{}{0ex}{}{N}{N-1}\right)\frac{1}{p(D)}\frac{1}{B(a,b)}& \text{(5.22)}\\ p(D)& =\left(\genfrac{}{}{0ex}{}{N}{N-1}\right)\frac{B(a+N_1,b+N_0)}{B(a,b)}& \text{(5.23)}\end{array}$$

$\beta$-伯努利分布模型(Beta-Bernoulli model)的边缘似然函数和上面的基本一样,唯一区别就是去掉了$\left(\genfrac{}{}{0ex}{}{N}{N-1}\right)$这一项.

5.3.2.2 狄利克雷-多重伯努利模型(Dirichlet-multinoulli model)

和上面$\beta$-伯努利模型类似,狄利克雷-多重伯努利模型(Dirichlet-multinoulli model)的边缘似然函数如下所示:
$p(D)=\frac{B(N+\alpha )}{B(\alpha )}$(5.24)
其中的
$B(\alpha )=\frac{{\prod }_{k=1}^K\Gamma ({\alpha }_k)}{\Gamma ({\Sigma }_k{\alpha }_k))}$(5.25)
把上面两个结合起来写成如下所示形式:
$p(D)=\frac{\Gamma ({\Sigma }_k{\alpha }_k)}{\Gamma (N+{\Sigma }_k{\alpha }_k)}{\prod }_k\frac{\Gamma (N_k+{\alpha }_k)}{\Gamma ({\alpha }_k)}$(5.26)
这个等式在后文中会有很多用处.

5.3.2.3 高斯-高斯-威沙特分布(Gaussian-Gaussian-Wishart model)

设想使用了一个共轭正态逆威沙特分布(NIW)的多元正态分布(MVN).设$Z_0$是先验的归一化项(normalizer),$Z_N$是后验的归一化项,$Z_t=(2\pi {)}^{ND/2}$是似然函数的归一化项.然后很明显就能发现:

$$\begin{array}{rlr}p(D)& =\frac{Z_N}{Z_0{Z}_1}& \text{(5.27)}\\ & =\frac{1}{{\pi }^{ND/2}}\frac{1}{2^{ND/2}}\frac{(\frac{2\pi }{k_N}{)}^{D/2}|S_N{|}^{-v_N/2}{2}^{(v_0+N)D/2}{\Gamma }_D(v_N/2)}{(\frac{2\pi }{k_0}{)}^{D/2}|S_0{|}^{-v_0/2}{2}^{v_{0}D/2}{\Gamma }_D(v_0/2)}& \text{(5.28)}\\ & =\frac{1}{{\pi }^{ND/2}}(\frac{k_0}{k_N}{)}^{D/2}\frac{|S_0{|}^{-v_0/2}{\Gamma }_D(v_N/2)}{|S_N{|}^{-v_N/2}{\Gamma }_D(v_0/2)}& \text{(5.29)}\end{array}$$

这个等式后面也会用得上.

5.3.2.4 对数边缘似然函数的贝叶斯信息标准估计(BIC approximation to log marginal likelihood)

一般来说,直接计算等式5.13里面的积分还挺难的.一种简单又流行的近似方法是使用贝叶斯信息量(Bayesian information criterio,缩写为BIC),形式如下所示(Schwarz 1978):

$BIC\stackrel{△}{=}\log p(D|\hat{\theta })-\frac{dof(\hat{\theta })}{2}\log N\approx \log p(D)$(5.30)

上式中的$dof(\hat{\theta })$是模型中的自由度个数(number of degrees of freedom),而$\hat{\theta }$是模型的最大似然估计(MLE).这有一种类似惩罚对数似然函数(penalized log likelihood)的形式,其中的惩罚项(penalty term)依赖于模型的复杂度.具体信息可以从本书8.4.2查看贝叶斯信息量评分的推导过程.

以一个线性回归为例.如本书7.3所示,最大似然估计为$\hat{w}=(X^{T}X{)}^{-1}{X}^{T}y$, ${\hat{\sigma }}^2=RSS/N$,$RSS={\sum }_{i=1}^N(y_i-{\hat{w}}_{mle}^T{x}_i{)}^2$.对应的对数似然函数为:

$\log p(D|\hat{\theta })=-\frac{N}{2}\log (2\pi {\hat{\sigma }}^2)-\frac{N}{2}$(5.31)

因此对应的贝叶斯信息量(BIC)评分为(去掉了常数项):
$BIC=-\frac{N}{2}\log ({\hat{\sigma }}^2)-\frac{D}{2}\log (N)$(5.32)

其中的Ｄ是模型中的变两个数．在统计学中，通常对BIC有另外的一种定义,称之为贝叶斯信息量损失(BIC cost,因为目的是将其最小化):
$BIC-cost\stackrel{△}{=}-2\log p(D|\hat{\theta })+dof(\hat{\theta })\log (N)\approx -2\log p(D)$(5.33)

在线性回归的情况下,这就变成了:
$BIC-cost=N\log ({\hat{\sigma }}^2)+D\log (N)$(5.34)

贝叶斯信息量(BIC)方法非常类似于最小描述长度原则(minimum description length,缩写为MDL),这个原则是根据模型拟合数据的程度以及定义复杂度来对模型进行评分.更多细节参考(Hansen and Yu 2001).

还有一个和BIC/MDL非常相似的概念叫做赤池信息量(Akaike information criterion,缩写为AIC),定义如下所示:
$AIC(m,D)\stackrel{△}{=}\log p(D|{\hat{\theta }}_{MLE})-dof(m)$(5.35)

这个概念是从频率论统计学的框架下推导出来的,不能被解释为对边缘似然函数的近似.虽然它的形式和BIC很相似.可以看出AIC当中的惩罚项(penalty)要比BIC里面小.这就导致了AIC会挑选比BIC更复杂的模型.不过这也会导致更好的预测精度.具体参考(Clarke et al. 2009, sec 10.2)来了解更多讨论以及这类信息量.

5.3.2.5 先验的效果

有时候咱也不知道该怎么设置先验.在进行后验推导的时候,先验的细节可能也不太重要,因为经常是似然率(likelihood)总会覆盖了先验.不过当计算边缘似然函数的时候,先验扮演的角色就重要多了,因为要对所有可能的参数设定上的似然函数进行平均,然后用先验来做权重.

图5.7和5.8所示的是线性回归的模型选择问题,使用了先验$p(w0=N(0,{\alpha }^{-1}I)$.其中的$\alpha$是一个用来控制先验强度的调节参数.这个参数效果很大,具体参考本书7.5所属.只管来说,如果$\alpha$很大,意味着权重被"强迫"降低,所以对于一个复杂模型需要使用很多小参数来拟合数据(比如高维度多项式拟合).反过来如果$\alpha$很小,就更倾向于使用简单模型,因为每个参数都可以放大很多倍.

如果先验未知,那么正确的贝叶斯过程就是先对先验给出一个先验.也就是对超参数(hyper-parameter)$\alpha$和参数w给出一个先验.要计算边缘似然函数,就要对所有未知量进行积分,也就是要计算:

$p(D|m)=\int \int p(D|w)p(w|\alpha ,m)p(\alpha |m)dwd\alpha$(5.36)

当然,这就需要实现制定一个超先验(hyper-prior,即对先验的先验).好在在贝叶斯层次(Bayesian hierarchy)中越高的层次就对先验设置越不敏感.所以通常就是用无信息的超先验.

计算的一个捷径就是对$\alpha$进行优化,而不是去积分.也就是用下面的近似:

$p(D|m)\approx \int p(D|w)p(w|\hat{\alpha },m)dw$(5.37)

其中的

$\hat{\alpha }=\arg {\max }_{\alpha }p(D|\alpha ,m)=\arg {\max }_{\alpha }\int p(D|w)p(w|\alpha ,m)dw$(5.38)

这个方法就叫做经验贝叶斯(empirical Bayes,缩写为EB),更多相关细节在本书5.6.这正是图5.7和5.8中所用的方法.

贝叶斯因数(Bayes factor,BF(1,0))	解析
BF<1/100	$M_0$决定性证据
BF<1/10	$M_0$强证据
1/10<BF<1/3	$M_0$中等证据
1/3<BF<1	$M_0$弱证据
1<BF<3	$M_1$弱证据
3<BF<10	$M_1$中等证据
BF>10	$M_1$强证据
BF>100	$M_1$决定性证据

表格5.1 Jeffrey 对贝叶斯因数的证据规模解析

5.3.3 贝叶斯因数(Bayes factors)

设模型先验是均匀分布的,即$p(m)\propto 1$.那么这时候模型选择就等价于选择具有最大边缘似然率的模型了.接下来假设有两个模型可选,分别是空假设(null hypothesis)$M_0$和替换假设(alternative hypothesis)$M_1$.然后就可以定义边缘似然函数之比就叫做贝叶斯因数(Bayes factor):

$B{F}_{1,0}\stackrel{△}{=}\frac{p(D|M_1)}{p(D|M_0)}=\frac{p(M_1|D)}{p(M_0|D)}/\frac{p(M_1)}{p(M_0)}$(5.39)

(这个跟似然率比值(likelihood ratio)很相似,区别就是整合进来了参数,这就可以对不同复杂度的模型进行对比了.)如果$B{F}_{1,0}>1$,我们就优先选择模型1,反之就选择模型0.

当然了,也可能这个$B{F}_{1,0}$就只比1大一点点.这时候也不能确信模型1就一定更好.Jeffreys(1961)提出了一系列的证据范围来解析贝叶斯因数的不同值,如表格5.1所示.这个大概就相当于频率论统计学中的p值(p-value)在贝叶斯统计学中的对应概念.或者也可以把这个贝叶斯因数转换成对模型的后验.如果$p(M_1)=p(M_0)=0.5$,则有:

$p(M_0|D)=\frac{B{F}_{0,1}}{1+B{F}_{0,1}}=\frac{1}{B{F}_{1,0}+1}$(5.40)

5.3.3.1 样例:测试硬币是否可靠

加入我们观察了一些抛硬币试验,然后想要判断所用硬币是否可靠,可靠的意思就是两面朝上的概率都是一半,即有$\theta =0.5$,不可靠就是$\theta$可以在[0,1]中间的任意位置取值了.咱们把两种模型表示为$M_0,M_1$.$M_0$下的边缘似然函数为:

$p(D|M_{)}=(\frac{1}{2}{)}^N$(5.41)

其中的N就是抛硬币次数.然后$M_1$下的边缘似然函数使用一个$\beta$分布先验:

$p(D|M_1)=\int p(D|\theta )p(\theta )d\theta =\frac{B({\alpha }_1+N_1,{\alpha }_0+N_0)}{B({\alpha }_1,{\alpha }_0)}$(5.42)

此处参考原书图5.9

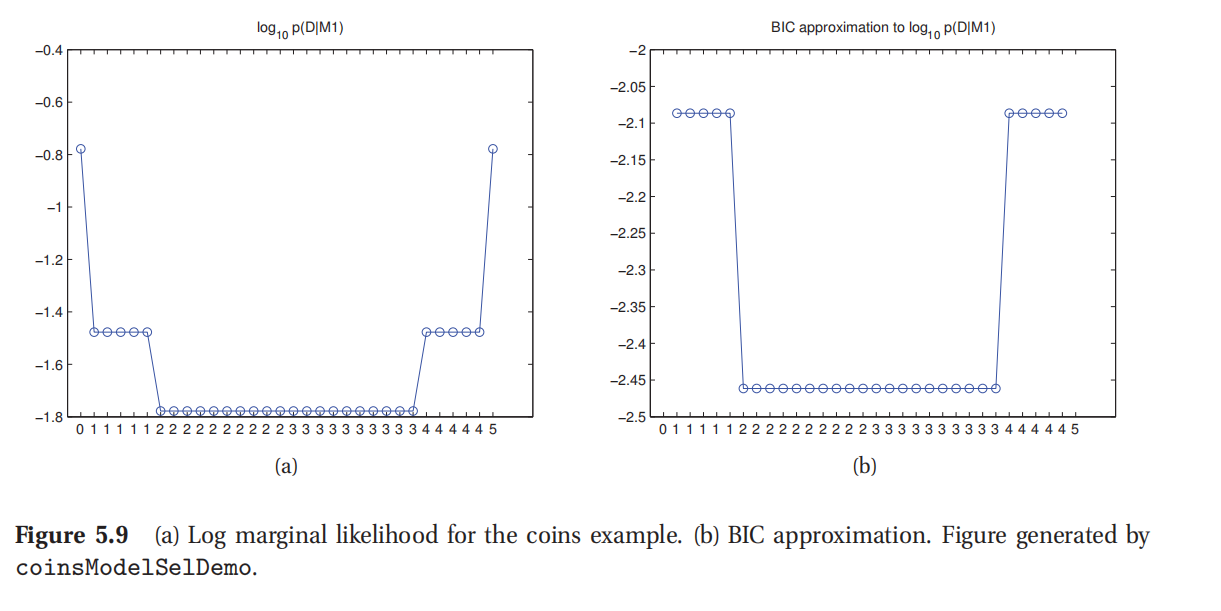
对$\log p(D|M_1)$和人头朝上次数$N_1$的关系进行投图得到了图5.9(a),设$N=5,{\alpha }_1={\alpha }_0=1$.(这个曲线的形状对${\alpha }_0,{\alpha }_1$并不敏感,因为这两个相等了.)如果观察到了两次或者三次人头朝上,那么就更倾向认为硬币没问题,即$M_0$的概率大于$M_1$,因为$M_0$是个更简单的模型(没有自由参数).如果硬币有问题而出现人头背面各自一半情况只是碰巧就是很可疑的巧合了.不过随着次数越来越极端,就可能更倾向硬币有问题的假设了.如果把贝叶斯因数的对数函数$\log B{F}_{1,0}$投图,会发现有一样的形状,因为$\log p(D|M_0)$是一个常量(constant).参考练习3.18.

图5.9(b)是对$\log p(D|M_1)$的贝叶斯信息量(BIC)估计,这个不可靠的硬币样例参考本书5.3.3.1.很明显这个曲线几乎和对数边缘似然函数的形状一模一样,这对于模型选择的目的来说就足够用了,因为绝对范围都没有影响.具体来说就是倾向于用更简单的模型,除非数据本身特别支持更复杂的模型.

5.3.4 杰弗里斯 - 林德利悖论(Jeffreys-Lindley paradox)*

当使用不适当先验(improper priors,比如积分不为1的先验)来进行模型选择和假设测试的时候,会遇到各种问题,即便这些先验对于其他目的来说可能还是可用的.例如,假如测试假设$M_0:\theta \in {\Theta }_0$和$M_1:\theta \in {\Theta }_1$.要定义在$\theta$上的边缘分布密度(marginal density),使用下面的混合模型:

$p(\theta )=p(\theta |M_0)p(M_0)+p(\theta |M_1)p(M_1)$(5.43)

只有当$p(\theta |M_0),p(\theta |M_1)$都是适当(归一化)的密度函数的时候,上式才有意义.这种情况下,后验为:

$$\begin{array}{rlr}p(M_0|D)& =\frac{p(M_0)p(D|M_0)}{p(M_0)p(D|M_0)+p(M_1)p(D|M_1)}& \text{(5.44)}\\ & =\frac{p(M_0){\int }_{{\Theta }_0}p(D|\theta )p(\theta |M_0)d\theta }{p(M_0){\int }_{{\Theta }_0}p(D|\theta )p(\theta |M_0)d\theta +p(M_1){\int }_{{\Theta }_1}p(D|\theta )p(\theta |M_1)d\theta }& \text{(5.45)}\end{array}$$

然后假设使用了不适当先验,即有$p(\theta |M_0)\propto c_0,p(\theta |M_1)\propto c_1$.则:

$$\begin{array}{rlr}p(M_0|D)& =\frac{p(M_0)c_0{\int }_{{\Theta }_0}p(D|\theta )d\theta }{p(M_0)c_0{\int }_{{\Theta }_0}p(D|\theta )d\theta +p(M_1)c_1{\int }_{{\Theta }_1}p(D|\theta )d\theta }& \text{(5.46)}\\ & =\frac{p(M_0)c_0{l}_0}{p(M_0)c_0{l}_0+p(M_1)c_1{l}_1}& \text{(5.47)}\end{array}$$

上式中$l_i={\int }_{{\Theta }_i}p(D|\theta )d\theta$是模型i的整合/边缘似然函数(integrated or marginal likelihood).然后设$p(M_0)+p(M_1)=\frac{1}{2}$.则有:

$p(M_0|D)=\frac{c_0{l}_0}{c_0{l}_0+c_1{l}_1}=\frac{l_0}{l_0+(c_1/c_0)l_1}$(5.48)

然后就可以任意选择$c_1,c_0$来改变后验.要注意,如果使用了适当(proper)但很模糊(vague)先验也能导致类似问题.具体来说,贝叶斯因数总会倾向于选择更简单的模型,因为使用非常分散的先验的复杂模型观察到数据的概率是非常小的.这就叫做杰弗里斯 - 林德利悖论(Jeffreys-Lindley paradox).

所以在进行模型选择的时候选择适当先验是很重要的.不过还是要注意,如果$M_0,M_1$在参数的一个子集上分享了同样的先验,那么这部分先验就可能是不适当的,因为对应的归一化常数会被约掉无效.