手术的最优化分配（5）——随机规划模型的上下界

上篇实现了随机规划模型后，这篇谈一谈如何收缩随机规划的解空间以加快求解速率。首先为了便于理解我们将手术分配的表格绘制出来：

	X1=	X2=	X3=	X4=
y1
y2
y3
y4
y5
y6
y7				​
y8
y9
y10
加班时长	o11=	o12=	o13=	o14=
	o21=	o22=	o23=	o24=
	o33=	o32=	o33=	o34=

有颜色的格子是决策变量，随机规划的目的是找到一种分配方式，使得所有场景下的总成本最小，此时每种场景都对应着一种不同的加班方案。

首先，在确定性模型(DORA)中的打破对称性方法适用于随机规划版本，打破对称性详见“手术的最优化分配（2）——打破对称性的约束(Symmetry-Breaking Constraints) (qq.com)”。

手术室开放数的上下限

与“手术的最优化分配（3）——手术室开放数目上下限及手术分配的启发式算法 (qq.com)”中原理类似，随机规划模型中手术室开放的上下限为：

其中，\overline{d_i} (di上划线) 表示此时所有场景中每个d_i对应的最大取值，\underline{d_i} (di下划线)表示所有场景中d_i的最小取值，例如在上一章的例子中，十台手术三个场景，则第五行和第六行分别为此时的\overline{d_i}和\underline{d_i}：

d1	210	151	148	167	149	245	235	233	229	180
d2	133	199	119	283	136	87	235	250	258	199
d3	120	123	187	167	242	163	214	207	235	85
_di	210	199	187	283	242	245	235	250	258	199
di_	120	123	119	167	136	87	214	207	229	85

由于原理与确定模型中上下限基本类似，此处不再赘述。

目标函数(成本)的上下限

此时假设μi为第i台手术在所有场景下的平均值，例如上表中μ_1为（210+133+120）/ 3  =154.33，则此时总成本的上下限为：

不等式的左侧很好理解,c^f为开放一间手术室的固定成本，其他部分为开放手术室数目的下限，即此时假设开放最少的手术室且不带有任何加班，当然成本是最小的。

不等式的最右侧则可以理解为只开放一间手术室，且所有手术都在加班时完成，故而成本最大。

右侧的证明过程如下：

从(19)到(20)的主要思想为：任何场景下，仅开放一间手术室的成本都是最高的。假如在某场景下需要开2间以上的手术室，则只开放一间手术室会导致大量的加班；某场景下最优解只需要开放一间手术室，则成本等于开放一间手术室(什么废话文学?)。此时仅开放一间手术室的数学表示为

手术室开放数目的上限2

手术室开放数目的第二个上限为

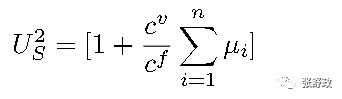
证明过程如下：

根据目标函数z的表达式和上一部分推导出的目标函数上限，可写出下式：

此处m^*为最优的手术室开放数目，则不等式左边为成本的上限，右侧为最优的成本。红框内为加班成本x期望加班时长，为非负数​。所以不等式右侧减去一个非负数依然小于左侧。

将剩下的不等式左右两侧同时÷c^f,则可得出

即为U_s^2

将以上四个式子和打破对称性约束加入随机规划模型后，可以大大提高求解效率​。篇幅所限就不在这里展示了，从下一篇开始我们会进入文中真正的重头戏——鲁棒优化部分​。虽然我还没有学相关内容，但是敬请期待​！