伽罗华域(Galois Field，GF，有限域)乘法运算

最近在做毕设，在看RS编码原理时，关于其乘法运算一直没看明白，文献也没有细说，今天发现一篇博客，看完之后豁然开朗，特地将此博客转载了过来，略作补充，红色为补充内容。

原文地址：http://blog.csdn.net/mengboy/article/details/1514445

GF(2^m)域

当m=8时，本原多项式为P(x) = x⁸ + x⁴ +x³ + x² + 1 .

这个很重要，因为一切化解都来源与此式。

在伽罗华域中,加法等同于对应位异或,所以

现在把α定义为P(x) = 0的根，即
　　　　α⁸＋α⁴＋α³＋α²＋1 = 0
　　　　即可以得到 α⁸=α⁴＋α³＋α²＋1，因为在珈罗华域中加法为模2加法，实际上是异或操作，所有有此2个等式同时成立。

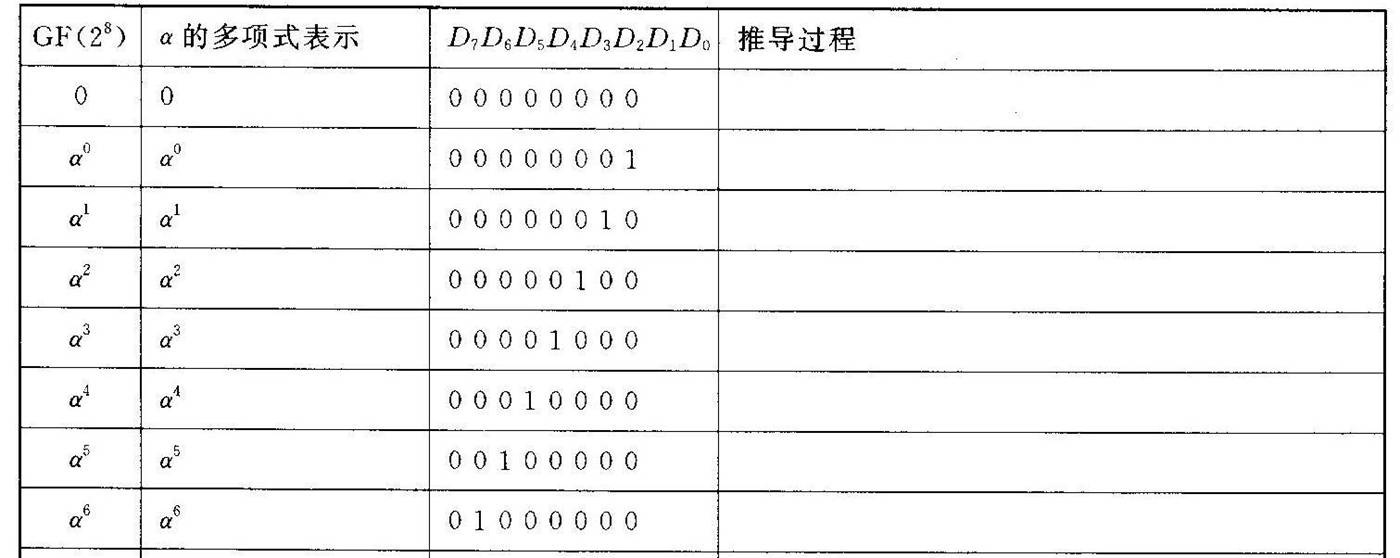
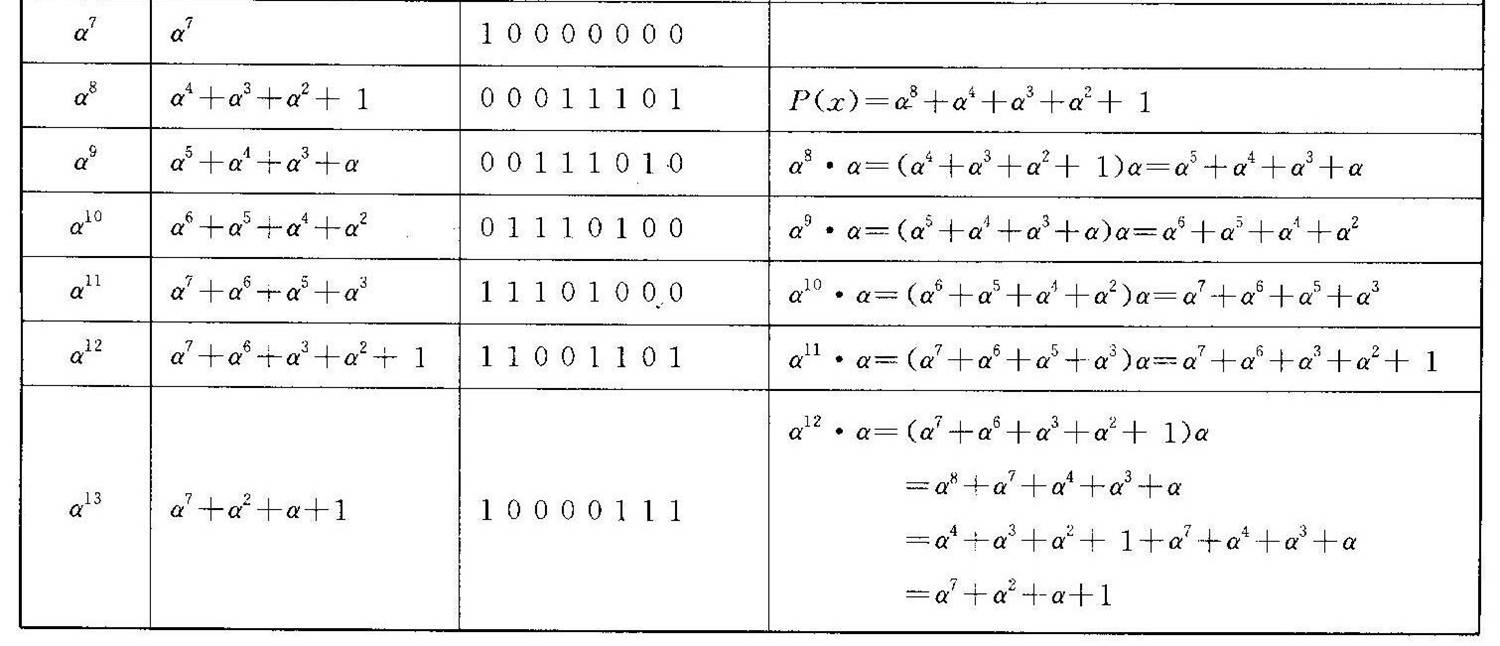
接着先给出下表付推导过程

 

 下面就按以下规则进行乘法运算 

  0=000   就是0     
  1=001   就是1   
  2=0010就是x+0=x   （此处及下文的x，其实就是表中的primitive element α）
  3=0011就是x+1   
  4=00100就是x^2   
  然后对于两个变量   
  u,v   
  可以先计算两个对应多项式的乘积（需要注意的是加法是模2的，或者说是异或运算），   
  比如   
  3*7=(x+1)*(x^2+x+1)=x*x^2+x*x+x+x^2+x+1=x^3+1   (模2运算中x+x=0   and   x^2+x^2=0)   
  所以3*7=9   （伽罗华域中乘法运算其实是域中元素对应的多项式的乘法运算，相加时为模2加法）
  在乘积得出来的多项式次数大于7时，我们需要对多项式在GF(2)上关于h(x)（h(x)就是本原多项式P(x)）求余数，也就是   
  129*5=(x^7+1)*(x^2+1)=x^9+x^7+x^2+1   
  将上面的函数加上x*h(x) （h(x)就是本原多项式P(x)）可以消去x^9,（其实就是手工除法过程，只是现在每一次商总是0或1），所以   
  129*5=x^9+x^7+x^2+1+x^9+x^5+x^4+x^3+x=x^7+x^5+x^4+x^3+x^2+x+1   
  =0010111111=191