GF(2m)域
当m=8时,本原多项式为P(x) = x8 + x4 +x3 + x2 + 1
在伽罗华域中,加法等同于对应位异或
现在把α定义为P(x) = 0的根,即
α8+α4+α3+α2+1 = 0即可以得到α8=α4+α3+α2+1乘法运算
3*7=(x+1)*(x^2+x+1)=x*x^2+x*x+x+x^2+x+1=x^3+1(模2运算中x+x=0 and x^2+x^2=0)
所以3*7=9在乘积得出来的多项式次数大于7时,我们需要对多项式在GF(2)上关于h(x)求余数,也就是
129*5=(x^7+1)*(x^2+1)=x^9+x^7+x^2+1
将上面的函数加上x*h(x)可以消去x^9,(h(x)即为p(x)),所以
129*5=x^9+x^7+x^2+1+x^9+x^5+x^4+x^3+x=x^7+x^5+x^4+x^3+x^2+x+1=0010111111=191
- 计算:{57} • {83} = {c1}
最后一步,先+x^5*p(x),按照异或规则消去x^13,x^9,x^8,x^6,x^5后再+x^3*p(x),消去x^11等,最后得到结果








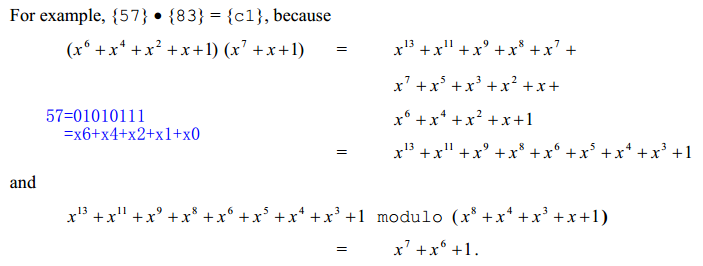
















 4万+
4万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








