距离和相似性度量

最新推荐文章于 2025-05-09 10:32:43 发布

beta2

最新推荐文章于 2025-05-09 10:32:43 发布

阅读量2.1w

点赞数 1

文章标签： distance 算法文档搜索引擎任务扩展

本文链接：https://blog.csdn.net/beta2/article/details/5045020

版权

本文介绍了距离和相似性度量在聚类、搜索引擎等任务中的重要性，并详细讨论了欧氏距离、余弦相似性、Pearson相关系数、Jaccard指数、编辑距离等常见度量方法。这些度量方法在处理向量、文档、字符串等问题时具有广泛应用，例如在搜索引擎的查询与文档匹配中，以及文本重复检测中。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

相似性度量或者距离函数对于像聚类，邻域搜索这样的算法是非常重要的。前面也提到，网页去重复也是相似性应用的一个例子。然而，如何定义个合适的相似或者距离函数，完全依赖于手头的任务是什么。一般而言，定义一个距离函数d(x,y),需要满足以下几个准则：

1. d(x,x) = 0 ;//到自己的距离为0
2. d(x,y)>=0 // 距离要非负
3. 对称性，d(x,y) = d(y,x) //如果A到B距离是a，那么B到A的距离也应该是a
4. 三角形法则(两个之和大于第三边） d(x,k)+ d(k,y) >= d(x,y)

满足这4个条件的距离函数很多，一般有几类是比较常见的，通常来自比较直观的形象，如平面的一个两点的直线距离。下面讨论应用比较广泛的几类距离或相似性度量函数，欧拉距离，余弦函数cosine，Pearson函数，Jaccard index，edit distance。如果一个对象d(如：一篇文档）表示成一个n维的向量（d1,d2,….,dn),每一个维度都为对象的一个特征，那么这些度量函数极容易得到应用。

1.范数和欧拉距离
欧拉距离，来自于欧式几何（就是我们小学就开始接触的几何学），在数学上也可以成为范数。如果一个对象对应于空间的一个点，每一个维度就是空间的一个维度。特殊情况，如果n=1，那么，小学我们就学过，直线上两个点的距离是|x1-x2|。推广到高纬情况，一个很自然的想法是，把每一个维度的距离加起来不就可以呢。这就形成了传说中的一范数：

$= /sum_{i=1}^n /left| x_i - y_i /right|$

看，是不是很简单。有一范数就有二范数，三范数。。。无穷范数。其实，二范数来的更加直观，我们都知道二维空间，三维空间的两点的距离公式。他就是二范数，在二维三维上的形式了。

$= /left( /sum_{i=1}^n /left| x_i - y_i /right|^2 /right)^{1/2}$

好了，一鼓作气,p范数(p-norm)

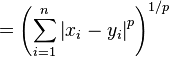
$= /left( /sum_{i=1}^n /left| x_i - y_i /right|^p /right)^{1/p}$
无穷范数：
$= /lim_{p /to /infty} /left( /sum_{i=1}^n /left| x_i - y_i /right|^p /right)^{1/p}$ $= /max /left(|x_1 - y_1|, |x_2 - y_2|, /ldots, |x_n - y_n| /right).$

空间两点的距离公式（2-范数），是最常用的距离公式，他就是传说中的欧拉距离。多简单。

2. cosine similarity
cosine similarity是备受恩宠啊，在学向量几何的时候，应该接触过这个神奇的公式

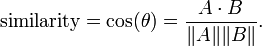
$/text{similarity} = /cos(/theta) = {A /cdot B /over /|A/| /|B/|}.$

分子是两个向量的点积，||A||是向量的长度，这个公式神奇的地方是，随着角度的变化的，函数是从-1，1变化的。向量夹角的余弦就是两个向量的相似度。cosine similarity 说，如果两个向量的夹角定了，那么无论一个向量伸长多少倍，他们的相似性都是不变的。所以，应用cosine 相似性之前，要把对象的每一个维度归一化。在搜索引擎技术中，cosine 相似性在计算查询和文档的相似性的时得到了很好的应用。对查询语句而言（如：“明天天气如何”），它的每一个维度是对应词的tf-idf.

cosine similarity的一个扩展是，Tonimoto系数：

$T(A,B) = {A /cdot B /over /|A/|^2 +/|B/|^2 - A /cdot B}.$

其实也没什么大不了。T（A,B）的分母是大于等于 cos similarity的分母，但且仅仅但 A,B长度一样是才相等。这就意味着，Tonimoto系数考虑了两个向量的长度差异，长度差异越大相似性约小。

3. Jacard index

Jacard 相似性直观的概念来自，两个集合有多相似，显然，Jacard最好是应用在离散的变量几何上。先看公式（不要头晕）

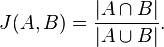
$J(A,B) = {{|A /cap B|}/over{|A /cup B|}}.$

分子是集合交集，分母是集合并集，画个图，马上就明白咋回事了。

和Jacard index 相似的一个公式是Dice‘ coefficient, 它也很直观，

$s = /frac{2 | X /cap Y |}{| X | + | Y |}$

4. Pearson correlation coefficient

学过概率论的人都知道，有均值，反差，还有相关系数，相关系数就是就是描述两组变量是否线性相关的那个东西。相关系数的优点是，它跟变量的长度无关，这个都点像cosine相似性。有一个应用是，比如一个商品推荐系统，要给用户A推荐相应的产品，首先要通过对商品的打分，找到与A相似k个用户。但是有些人，可能天生喜欢打高分，有些人偏向于打低分，为了消除这个问题相关系数是一个很好的度量方法。列公式，

$/rho_{X,Y}={/mathrm{cov}(X,Y) /over /sigma_X /sigma_Y} ={E[(X-/mu_X)(Y-/mu_Y)] /over /sigma_X/sigma_Y},$

这个公式貌似和cosine 是有点关系的。至于如何关联，我就不讨论了。参看correlation

5. 编辑距离或者Levenshtein distance

编辑距离说的两个字符串的相似程度。串A通过删除，增加，和修改变成串B的可以度量函数（一般是是通过多少步能将A变成B 也可以对每一个编辑步骤加权）wikipedia上有非常好的描述，这里就不再赘述。Levenshtein Distance. 与之相关的字符串相似性方法还有Jaro-Winkler distance。

6 SimRank 相似

SimRank来自图论，说两个变量相似，因为他们链接了同一个或相似的节点。这个算法需要需要重点讨论。下次在说。