概述
实际中很多应用不是寻找最优解,而是寻找一个根满足给定的约束条件,如果有n个非线性等式约束,就是本节介绍的非线性方程问题,本节主要介绍
1. 非线性方程的问题形式
2. 非线性方程的求解算法
3. 总结
非线性方程的问题形式
问题形式,寻找满足n个非线性等式的根,即
r(x)=0
其中 r(x)=[r1(x),...rn(x)]T
该问题可以转换为求解 min∑i=1...nr2i(x) ,根据最优化条件可知,最优解应该满足: ∇f(x∗)=0=>J(x∗)r(x∗)=0 。
1.该最小化问题等价于最小二乘问题,可以采用非线性最小二乘的求解算法,不同点在于有n个非线性等式。
2. 根据最优性条件,如果雅克比矩阵J(x)是非奇异的,则最优解就是该非线性方程的根;否则最优解可能不会满足r(x)=0
3. 如果对于病态的J(x),即如果秩为n-1或者n-2则最优化算法得到的解会比较差。
4. 最优化问题往往最优解只能得到一个,对于非线性方程可能存在唯一解、有限解、无穷解或者无解。
非线性方程的求解算法
该问题求解算法,主要思路是转换为最优化问题,利用类牛顿方法进行求解。
牛顿方法
类似于最优化问题的牛顿方法,寻找牛顿方向,然后不断迭代。算法如下:
算法流程
1. 每次寻找满足牛顿方程的方向进行迭代。
2. 牛顿方程来源,对r(x)进行泰勒展开,有r(x+p)=r(x)+J(x)p相当于定义一个线性模型近似该目标,即M(p)=r(x)+J(x)p
3. 牛顿方程来源二,看做是最优问题minf(x)=12||r(x)||2





 这篇博客介绍了非线性方程问题的形式和求解算法,包括牛顿方法及其局限性,改进算法如非精确牛顿方法、Broyden方法和Tensor方法,以及实际应用中的线搜索、信赖域策略和连续方法。重点讨论了如何通过最优化问题来解决非线性方程,并分析了各种方法在处理雅克比矩阵奇异或病态情况下的表现。
这篇博客介绍了非线性方程问题的形式和求解算法,包括牛顿方法及其局限性,改进算法如非精确牛顿方法、Broyden方法和Tensor方法,以及实际应用中的线搜索、信赖域策略和连续方法。重点讨论了如何通过最优化问题来解决非线性方程,并分析了各种方法在处理雅克比矩阵奇异或病态情况下的表现。
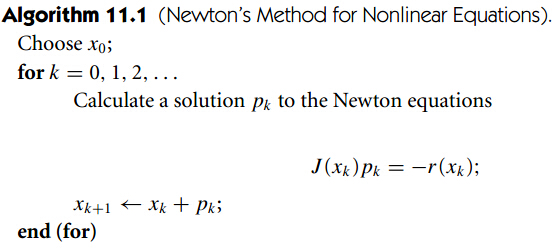
 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章


















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








