前言
在对我的数据科学与人工智能小组的新人进行小规模授课时讲课内容整理,有改动和删减.这可能是目前网络上最全面也最简单易懂的有关朴素贝叶斯的文章
有关贝叶斯的一些闲谈
无论是在生活中还是我们的科学理论中,经常会估计概率.比如,我们计算一下明天下雨的概率,或者中彩票的概率,或者其他概率.概率就是可能性.
但是在人工智能领域关于概率的问题却产生了两个不同的流派,那就是贝叶斯派和频率学派.频率学派认为万物发展尤其内在规律,我们要做的是找到那个固有的频率.而贝叶斯派则认为概率服从一定的分布,我们可以通过数据估计出来.不过这些差异并不算什么重点.我们今天要学贝叶斯派,简单点来说就是因为它有用,有用之处在哪里呢?
有用之处就在于我们可以求出逆向的概率,也就是我们知道了一个盒子里有三个白球,两个红球,另一个盒子里有三个红球,两个白球,我们随便从一个盒子里面拿出了一个红球,就可以反向求出这个红球最有可能是那个盒子里的.换个说法也就是你知道今天下雨了,那么你也就可以推测出昨天什么天气.当然了,除非你失忆了,不然你基本上知道昨天什么天气.——-不管话说回来,在现实情况中我们经常不知道一件事情的原因是什么,那么这个时候贝叶斯定理就有用了.而且是非常的有用.
前向概率与逆向概率
各位大一的萌新还没有学概率论,不过有些东西你们一定知道,那就是一个盒子里边有三个白球,两个红球,那么拿出一颗球,白球的概率是多少,红球的概率是多少.
答案很显然,白球五分之三,红球五分之二.五分之三加五分之二等于一,也就是百分之百会拿出来白球或者红球
那么又有一个箱子,里面有三个红球,两个白球,请问从两个箱子里拿出一个球,白球概率是多少,红球概率是多少.
答案也很显然,白球是(五加五)分之(三加二)等于二分之一,红球一样也是二分之一.
那么现在我们就可以反过来求球球了,假设我们拿出来了一颗白球,那么从第一个箱子里面拿出来白球的概率是多少?从第二个箱子里拿出来的概率是多少?
这个也很好算,反过来第一个箱子有三个白球,第二个箱子里边有两个白球,一共有五个白球,那么来自第一个箱子的概率也就是(三加二 )分(三),第二个箱子也就是五分之二.
那么这个白球最有可能从哪个盒子里拿出来呢?—第一个
这个时候,我们的贝叶斯定理其实就已经出来了,下面我们就可以把刚刚求逆概的语言抽象为数学语言,也就是数学公式表现出来了.
白球来自第一个盒子的概率 = 第一个盒子中白球的数量 / 所有白球的数量
这个时候我们要注意的是,我们虽然是使用数量来求解的,为了能够让这个公式更通用,我们把他转换为概率
p(白球来自第一个盒子) = p(第一个盒子中的白球) / p(白球)
然后我们再抽象一次,球的颜色是b,盒子是a,那么白球就是b1,盒子一就是a1.
但是仅仅是换个符号还是不够的,我们把盒子和白球的关系也用数学形式表现出了,比如白球来自于第一个盒子,也就是在 白球 的情况下,球来自第一个盒子的概率,我们记座盒子一|白球也就是a1|b1反过来第一个盒子中白球的比例也就是b1|a1,如果要具体求解的话,就使用乘法公式:p(b1|a1) = p(a1)*p(b1)
然后是第一个白球中的数量 ?(也就是全部球的数量 × 盒子一的比例 × 盒子一中白球的比例) / (全部球的数量 × 所有球中白球的比例)
数学公式也就是 n*p(a1)*p(b1|a1)/(n*p(b1) = p(a1)*p(b1|a1)/p(b1)
那么可得:
p(a1|b1) = p(a1)*p(b1|a1)/p(b1) = ((1/2) * (3/5)) / (1/2) = 3/5
这个时候我们的朴素贝叶斯定理已经出来一半了,那另一半是什么呢?那当然是朴素一下了,不过在那之前我们还是把上面的公式再抽象一下比较好
比如把a1抽象为xi,也就是任意特征,b1抽象为yi,也就是任意结果这样原公式也就可以计算无论多少个盒子多少个球的情况了,同时又因为我们要求的是概率最大的那个盒子,那么原公式也就可以改写为一下形式
y = arg max(y) P(yi)* p(x|yi)/p(x)
# 因为要挑选出的是概率最大的元素,那么这个时候坟墓p(x)起始就可以省略了.而假如有很多个属性呢? 这时候朴素贝叶斯的朴素的地方也就表现出来了,直接假设各个x是独立同分布的,也就是简单来说,扔钢镚,扔第一个钢镚正反面的概率都是二分之一,那么扔完了第一个钢镚,再扔第二个钢镚,正反面的概率还是二分之一,和第一个钢镚到底是正是反没有关系.那么俩钢镚同时扔反面的概率也就是二分之一乘以二分之一等于四分之一.
对应到我们的xi上来说,也就是管你x1是什么,x2的概率与你无关,这个时候我们要求计算他们的联合概率也就是相乘就可以了.那么这个时候我们就可以得到
拉普拉斯曾经说过:”概率论不过是对常识的数学抽象”
“拉普拉斯说的有道理”—-渥·兹基硕德
概率分布
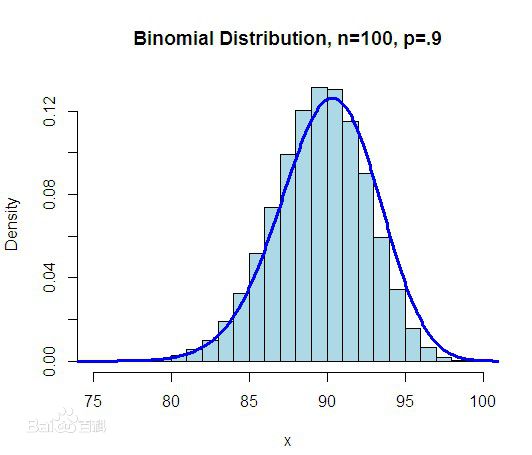
概率分布也就是y随x的变化规律,比如二项分布就是扔硬币的实验,要么为0,要么为1 ,而随着次数的变化,其规律也是在不断变化的.其变化方式大概是这样的.
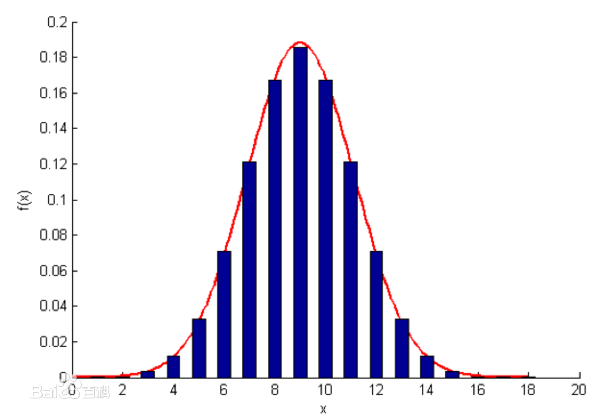
除此之外分布模式还有,高斯分布,其分布不仅与x有关与方差均值有关
以及多项分布,之前的小球的例子就是符合多项分布的例子,其概率是数量的直接比,
二项分布就是重复n次独立的伯努利试验。在每次试验中只有两种可能的结果,而且两种结果发生与否互相对立,并且相互独立,与其它各次试验结果无关,事件发生与否的概率在每一次独立试验中都保持不变,则这一系列试验总称为n重伯努利实验,当试验次数为1时,二项分布服从0-1分布。
朴素贝叶斯的极大似然估计与概率分布
大家现在可以观察一下,我们刚刚的贝叶斯公式,请问有没有发现什么问题.
很显然的问题就在于实际情况中,从x -> y的条件概率,其分布方式我们并不知道.
虽然p(y)我们可以直接得到,但是p(x|y)也就是在y的条件下,x证明分布我们并不清楚,可能x与y的关系是二项分布的,也可能是多项分布或者高斯分布的.这个时候我们就需要自己选择一个分布方式进行计算了.
那概率分布有那些呢?二项分布,多项分布,高斯分布.我们假设此时先验概率为多项式分布,那么此时参数 \theta_y 使用平滑过的最大似然估计法来估计,即相对频率计数:
图中特别的地方在于其中n个分子每个分子加了个参数a,分母也加了na,这是为了避免分子也就是n个x相乘的时候恰巧摸个x为零这种情况.因为这个时候会导致最后的结果为零,产生了误差.
但是恰好我们需要的最后结果为最大概率,按照公式的求解方式,我们给每个x加个a,分母加个na,那么最终大小关系不变,嗯哼,所以我们就采取了这种方式来解决误差问题.而当a等于1时,这种方式被称为拉普拉斯平滑.
“这是我说的”-拉普拉斯
“这话不是我说的”-鲁迅
至于其他的条件概率求解,则按照其他概率分布公式求得,比如高斯分布,参数 \sigma_y 和 \mu_y 使用最大似然法估计。:
亦或是二项分布:
那么问题来了,什么是极大似然估计呢???
其实极大似然估计就是按照现有观察数据中数量最多的数据作为结果.比如高斯分布中,虽然我们不知道方差和均值到底是多少,但是我们把我们观察到的数据当做实际需要的方差和均值来计算就好了.
比如我们扔硬币,扔一个很特别的硬币.正面的可能性为0.6,假如我们连扔了十次为一次实验,一共做四次实验,出现的实验结果为{3,5,7,8},虽然这个时候实际的概率还是0.6 ,但是问题就在于这个0.6我们是没有办法观察到的,假如上帝存在的话,那么可能上帝能做到,但是凡人有凡人的方式,我们可以使用我们的实验结果来估计这个概率,(3+5+7+8)/(10*4) =5.75,根据极大似然估计也就是最大可能性估计,我们就认为这个5.75是实际的概率.这样我们可以得到一个不错的近似结果
而随着实验的增加 我们的近似结果自然也会越来越靠近真实的概率.
误差分析
虽然我们之前所讲的朴素贝叶斯算法已经非常的优秀,在很多领域都有着出色的表现,然而其除了机器学习基本的常见误差以外,朴素贝叶斯本身的误差其实还是蛮大的.首先比如第一个,连乘误差.
我们的条件概率的分子是很多小数相乘,那么就可能会造成连乘误差,导致溢出.那么当特征值过多时,我们就可以采用对数似然,也就是log(y) = log(p(xi|y)然后各个相乘的小数就可以变成—>log(abc) = log(a)* log(b) * log(c)这样就没有小数连乘的误差问题了.
除此之外,算法本身的误差也是很大的,比如最基本的假设,”朴素”—>也就是特征的独立同分布,如果特征之间存在依赖关系,那么我们就可能需要其他的算法了.比如TAN,SPODE,AODE等等.
sklearn中的朴素贝叶斯分类器
sklearn文档原话如下:
相比于其他更复杂的方法,朴素贝叶斯学习器和分类器非常快。 分类条件分布的解耦意味着可以独立单独地把每个特征视为一维分布来估计。这样反过来有助于缓解维度灾难带来的问题。
另一方面,尽管朴素贝叶斯被认为是一种相当不错的分类器,但却不是好的估计器(estimator),所以不能太过于重视从
predict_proba 输出的概率。
sklearn中的朴素贝叶斯分类器
sklearn中的三种朴素贝叶斯分类器分别为高斯朴素贝叶斯分类器,多项分布朴素贝叶斯分类器,以及伯努利朴素贝叶斯分类器(对应二线分布)
其使用方法如下:
from sklearn.naive_bayes import GaussianNB
gnb = GaussianNB()
y_pred = gnb.fit(iris.data, iris.target).predict(iris.data)要注意的是其中,高斯朴素贝叶斯分类器没有参数可以调整,但是支持导入样本权重sample_weight函数,多项分布朴素贝叶斯分类器有一个参数先验平滑因子a,伯努利朴素贝叶斯分类器有先验平滑因子a与一个二值化参数binarize.
同时他们都支持增量训练方法:partial_fit函数
参考
[1] 机器学习 周志华教授
[2] sklearn 官方文档








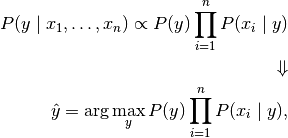
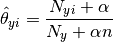
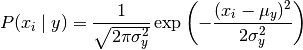
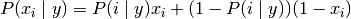

















 171
171

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










