吴恩达《深度学习工程师》Part1.Week3 浅层神经网络

3.1 神经网络概览
第2周的课程重点讲解了logistic回归模型，这周开始学习神经网络模型。神经网络的原理与logistic类似，只不过节点更多，且会重复多层。

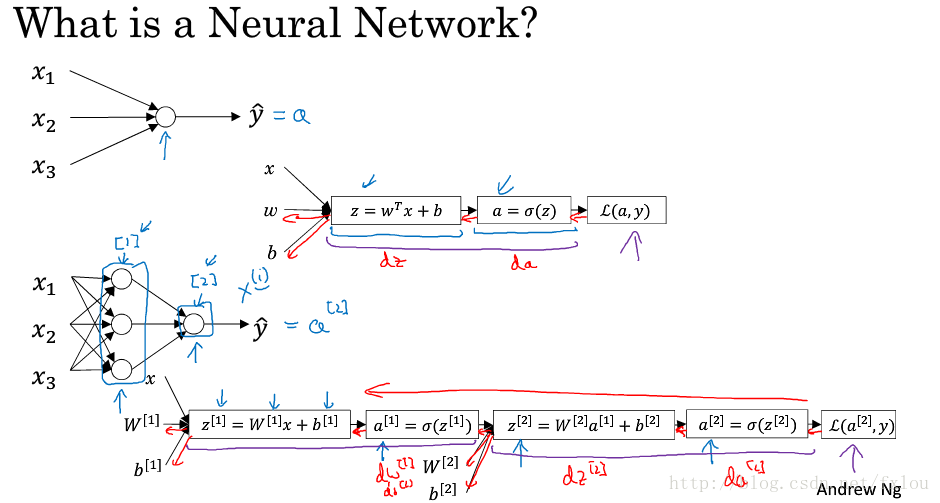
图1 logistic模型和神经网络模型

图1上面两个图是logistic模型，样本数据$x_1,x_2,x_3$输入到一个节点中，前向传播分别计算$z,a$以及损失函数$L(a,y)$。反向传播计算$da,dz,dw,db$，并用梯度下降法对$w$和$b$进行训练。

图1下面两个图是一个简单的神经网络模型，样本数据$x_1,x_2,x_3$输入到第一层的三个节点中，前向传播计算出$z^{[1]},a^{[1]}$，再进入到第二层的一个节点中，计算出$z^{[2]},a^{[2]}$，最后计算出损失函数$L(a,y)$。反向传播依次计算$da^{[2]},dz^{[2]}，dW^{[2]},db^{[2]}$，再计算$da^{[1]},dz^{[1]}，dW^{[1]},db^{[1]}$，用梯度下降法对$W^{[1]},b^{[1]},W^{[2]},b^{[2]}$进行更新。

3.2 神经网络表示
图2是个简单的神经网络模型。

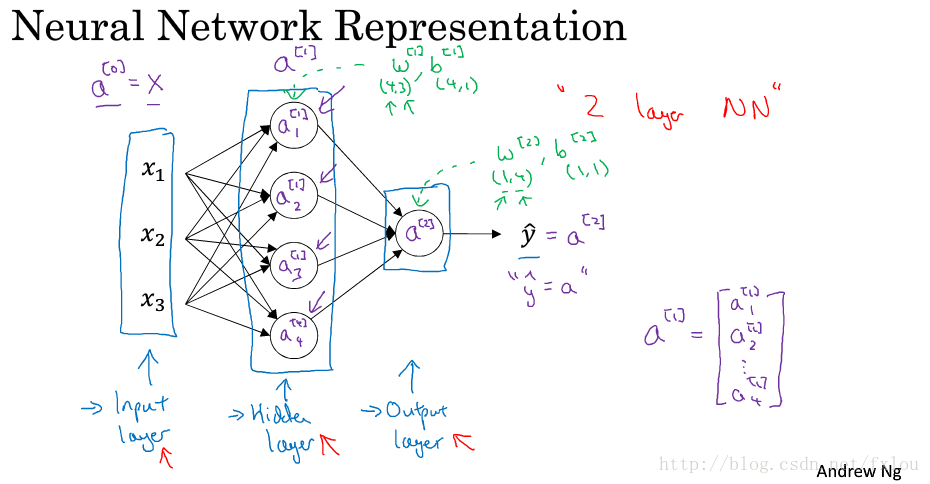
图2 神经网络模型
从左向右依次是输入层、隐藏层和输出层，每层的输出分别用 $a^{[0]},a^{[1]},a^{[2]}$表示，由于只有隐藏层和输出层有参数，而输入层一般不认为是一个标准层，在论文中常把这种神经网络模型归为2层神经网络。

3.3 计算神经网络的输出
单个训练样本的神经网络输出见图3所示。

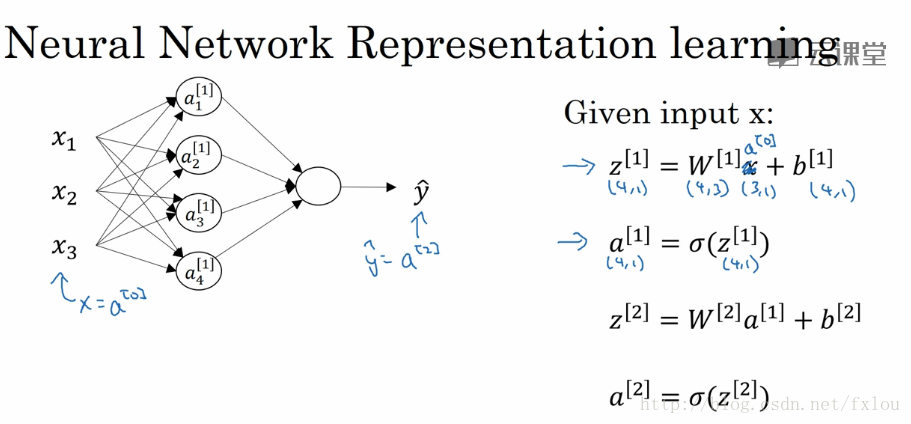
图3 神经网络输出的计算
各层的激活值计算见图3右侧公式
3.4 多个例子中的向量化
略
3.5 向量化实现的解释
略
3.6 激活函数
前面构建的神经网络使用的激活函数都是sigmoid函数。
$$sigmoid(z)=\frac{1}{1+e^{-z}}$$

实际上还有其他的激活函数，例如tanh函数。

$$tanh(z)=\frac{e^z-e^{-z}}{e^z+e^{-z}}$$

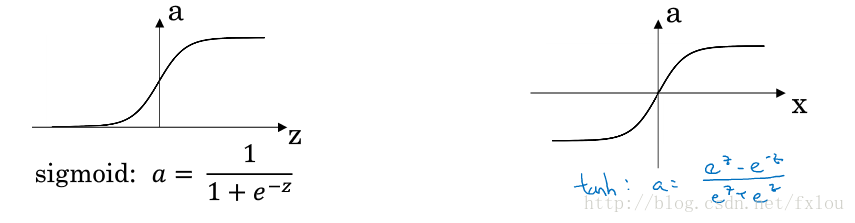
图4 sigmoid函数和tanh函数

tanh函数在各方面的表现都比sigmoid函数出色，tanh函数的平均值为0，如果需要数据均值为0的话，tanh函数更合适。在实际构建的神经网络中，很少将sigmoid函数用在隐藏层，而多采用tanh函数，除非最后的输出层要进行二分类的话，才会用sigmoid函数，因为sigmoid函数的输出值区间为0到1，更适合二分类问题。

无论是sigmoid函数还是tanh函数，当z值过大或过小时，两个函数的斜率都趋近于0，即进入饱和状态，用于梯度下降时，模型的训练效率极低。

一个更高效的激活函数时ReLU函数。

$$ReLU(z)=max(0,z)$$
当 $z<0$时，斜率为0，当 $z>0$时，斜率为1。当不确定隐藏层选取哪种激活函数时，可以考虑用ReLU函数。尽管ReLU函数在一半的z空间中斜率为0，但在实际训练时，效率还是很高的
还有一种函数是带泄漏的（Leaky）ReLU函数。
$$Leaky ReLU(z)=max(0.01z,z)$$
这种函数比ReLU函数效果更好，虽然使用没有那么高。

3.7 为什么需要非线性激活函数
如果不对每层的z采用非线性激活函数的话，无论构建的神经网络有多少次，最后的输出仍然时输入的线性组合，则整个神经网络将失效。

3.8 激活函数的导数
略

3.9 神经网络的梯度下降法
如图2所示的两层神经网络模型在进行前向传播时，有以下四个公式：
$Z^{[1]}=W^{[1]}\cdot X+b^{[1]}$
$A^{[1]}=g(Z^{[1]})$
$Z^{[2]}=W^{[2]}\cdot A^{[1]}+b^{[2]}$
$A^{[2]}=g(Z^{[2]})$
在进行反向传播时，有以下六个公式：
$dZ^{[2]}=A^{[2]}-Y$
$dW^{[2]}=\frac{1}{m}dZ^{[2]}\cdot A^{[1]T}$
$db^{[2]}=\frac{1}{m}\sum_1^mdZ^{[2]}$
$dZ^{[1]}=W^{[2]T}dZ^{[2]}\cdot g^{'}Z^{[1]}$
$dW^{[1]}=\frac{1}{m}dZ^{[1]}\cdot X^{T}$
$db^{[1]}=\frac{1}{m}\sum_1^mdZ^{[1]}$

3.10 直观理解反向传播
略

3.11 随机初始化
在初始化偏置时，如果简单地将其全部设置为0时，则每层的隐藏单元都是对称的，无论后期经过多少次的训练，各节点得到的函数都相同，实际上，我们想要不同的节点训练不同的函数，从而实现复杂的分析。

因此，可以采用随机初始化操作，用以下代码实现：

w_1=np.random.randn((n_1,n_x))*0.01
b_1=np.zeros((n_1,1))
'''
w_1是第一层隐藏层的权重，n_1是第一层的节点数，n_x是输入数据的纬度，
b_1是第一层隐藏层的偏置，由于偏置不存在对称性问题，可以将其初始化为0
'''

以上代码中的0.01是为了使得非线性函数的输入控制在距离0较小的范围，如果激活函数为sigmoid函数或tanh函数的话，这么做可以防止过大和过小的数值导致的梯度趋近于0的现象，如果激活函数时ReLU函数的话，就没有这个必要了。

在训练浅层神经网络时，0.01数值的设置没有什么问题，但是如果训练深层神经网络的话，可能需要多试几组其它的数值。