======================================================================
本系列博客主要参考 Scikit-Learn 官方网站上的每一个算法进行,并进行部分翻译,如有错误,请大家指正
转载请注明出处
======================================================================
K-means算法分析与Python代码实现请参考之前的两篇博客:
接下来我主要演示怎么使用Scikit-Learn完成K-means算法的调用
注明:本例分析是固定输入K值和输入k个初始中心点,这样做具有很大的局限性,容易陷入局部最优,可以利用其他算法(如canopy算法)进行粗聚类估计,产生n个簇,作为k-means的K值,这里不做详细说明
一:K-means聚类算法
1:K-means算法简介
聚类算法,数据挖掘十大算法之一,算法需要接受参数k和k个初始聚类中心,即将数据集进行聚类的数目和k个簇的初始聚类“中心”,结果是同一类簇中的对象相似度极高,不同类簇中的数据相似度极低
2:K-means算法思想和描述
思想: 以空间中k个中心点进行聚类,对最靠近他们的对象归类,通过迭代的方法,逐次更新各聚类中心
描述:
(1)适当选择C个类的初始中心
(2)在第K此迭代中,对任意一个样本,求其到C各中心的距离,将该样本归到距离最短的中心所在的类
(3)利用均值等方法更新该类的中心值
(4)对于所有的C个聚类中心,如果利用(2)(3)的迭代法更新后,值保持不变,则迭代结束,否则继续迭代
3:集合实例的简单介绍
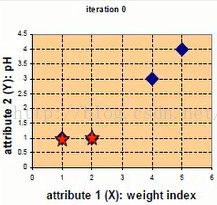
例如现在有四种药物A,B,C,D,他们分别有两个属性。如下图
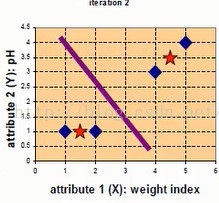
将他们表示在坐标轴上为:
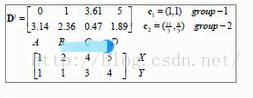
第一次迭代,随机选取两个点作为初始中心点,eg c1,c2作为初始中心点,D0中分别为四个点到两个样本点的距离,X,Y为横纵坐标
A点离第一个点最近,所以group-1行A点置1,剩下的三个点离第二个中心点最近,所以group-2行置1
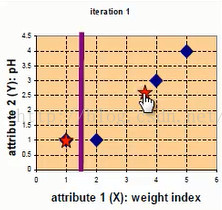
此时应该更新样本点,c1不变,c2更新为((2+4+5)/3,(1+3+4)/3)=(11/3,8/3),更新后的数据中心点如下图红点所示
第二次迭代,以(11/3,8/3)作为样本中心点,分别计算四个点到样本中心点的距离,如下:
A,B点距离第一个中心点最近,C,D点距离第二个中心点最近,所以group-1行,A,B置1,group-2行C,D置1
此时重新更新样本中心点,c1=((1+2)/2,(1+1)/2)=(3/2,1),c2=((4+5)/2,(3+4)/2)=(9/2,7/2),更新后的数据中心点如下图红点所示
第三次迭代,计算同上,略过,此时数据的样本中心点不再发生变化,所以可以停止迭代,最终聚类情况如下:
4:下边看一个使用sklearn.Kmeans的实例(实例来源)
实例说明:利用sklearn.datasets.make_blobs产生1500条两维的数据集进行不同情况下的聚类示例,代码如下
<span style="font-size:18px;">#coding:utf-8
'''
Created on 2016/4/25
@author: Gamer Think
'''
import numpy as np #科学计算包
import matplotlib.pyplot as plt #python画图包
from sklearn.cluster import KMeans #导入K-means算法包
from sklearn.datasets import make_blobs
plt.figure(figsize=(12, 12))
'''
make_blobs函数是为聚类产生数据集
产生一个数据集和相应的标签
n_samples:表示数据样本点个数,默认值100
n_features:表示数据的维度,默认值是2
centers:产生数据的中心点,默认值3
cluster_std:数据集的标准差,浮点数或者浮点数序列,默认值1.0
center_box:中心确定之后的数据边界,默认值(-10.0, 10.0)
shuffle :洗乱,默认值是True
random_state:官网解释是随机生成器的种子
更多参数即使请参考:http://scikit-learn.org/dev/modules/generated/sklearn.datasets.make_blobs.html#sklearn.datasets.make_blobs
'''
n_samples = 1500
random_state = 170
X, y = make_blobs(n_samples=n_samples, random_state=random_state)
# Incorrect number of clusters
y_pred = KMeans(n_clusters=2, random_state=random_state).fit_predict(X)
plt.subplot(221) #在2图里添加子图1
plt.scatter(X[:, 0], X[:, 1], c=y_pred) #scatter绘制散点
plt.title("Incorrect Number of Blobs") #加标题
# Anisotropicly distributed data
transformation = [[ 0.60834549, -0.63667341], [-0.40887718, 0.85253229]]
X_aniso = np.dot(X, transformation) #返回的是乘积的形式
y_pred = KMeans(n_clusters=3, random_state=random_state).fit_predict(X_aniso)
plt.subplot(222)#在2图里添加子图2
plt.scatter(X_aniso[:, 0], X_aniso[:, 1], c=y_pred)
plt.title("Anisotropicly Distributed Blobs")
# Different variance
X_varied, y_varied = make_blobs(n_samples=n_samples,
cluster_std=[1.0, 2.5, 0.5],
random_state=random_state)
y_pred = KMeans(n_clusters=3, random_state=random_state).fit_predict(X_varied)
plt.subplot(223)#在2图里添加子图3
plt.scatter(X_varied[:, 0], X_varied[:, 1], c=y_pred)
plt.title("Unequal Variance")
# Unevenly sized blobs
X_filtered = np.vstack((X[y == 0][:500], X[y == 1][:100], X[y == 2][:10]))
y_pred = KMeans(n_clusters=3, random_state=random_state).fit_predict(X_filtered)
plt.subplot(224)#在2图里添加子图4
plt.scatter(X_filtered[:, 0], X_filtered[:, 1], c=y_pred)
plt.title("Unevenly Sized Blobs")
plt.show() #显示图</span>
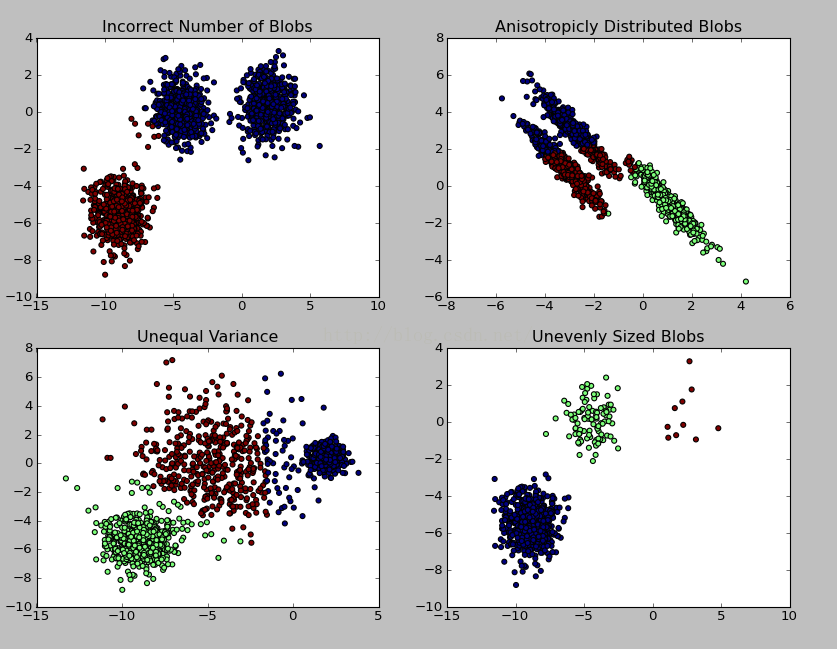
结果图示:
二:Mini Batch K-Means算法
scikit-learn官网上对于Mini Batch K-Means算法的说明如下:
Mini Batch K-Means算法是K-Means算法的变种,采用小批量的数据子集减小计算时间,同时仍试图优化目标函数,这里所谓的小批量是指每次训练算法时所随机抽取的数据子集,采用这些随机产生的子集进行训练算法,大大减小了计算时间,与其他算法相比,减少了k-均值的收敛时间,小批量k-均值产生的结果,一般只略差于标准算法。
该算法的迭代步骤有两步:
1:从数据集中随机抽取一些数据形成小批量,把他们分配给最近的质心
2:更新质心
与K均值算法相比,数据的更新是在每一个小的样本集上。对于每一个小批量,通过计算平均值得到更新质心,并把小批量里的数据分配给该质心,随着迭代次数的增加,这些质心的变化是逐渐减小的,直到质心稳定或者达到指定的迭代次数,停止计算
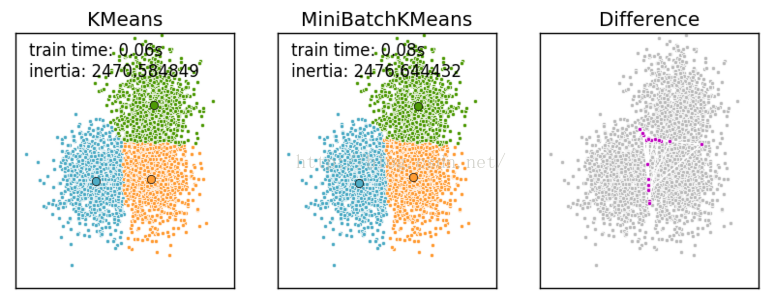
Mini Batch K-Means比K-Means有更快的 收敛速度,但同时也降低了聚类的效果,但是在实际项目中却表现得不明显
这是一张k-means和mini batch k-means的实际效果对比图
下边给出显示上边这副图的代码,也是对K-Means和Mini Batch K-Means算法的一个比较:
<span style="font-size:18px;">#coding:utf8
'''
Created on 2016/4/26
@author: Gamer Think
'''
import time
import numpy as np
import matplotlib.pyplot as plt
from sklearn.cluster import MiniBatchKMeans, KMeans
from sklearn.metrics.pairwise import pairwise_distances_argmin
from sklearn.datasets.samples_generator import make_blobs
##############################################################################
# Generate sample data
np.random.seed(0)
batch_size = 45
centers = [[1, 1], [-1, -1], [1, -1]] #初始化三个中心
n_clusters = len(centers) #聚类的数目为3
#产生3000组两维的数据,以上边三个点为中心,以(-10,10)为边界,数据集的标准差是0.7
X, labels_true = make_blobs(n_samples=3000, centers=centers, cluster_std=0.7)
##############################################################################
# Compute clustering with Means
k_means = KMeans(init='k-means++', n_clusters=3, n_init=10)
t0 = time.time() #当前时间
k_means.fit(X)
#使用K-Means 对 3000数据集训练算法的时间消耗
t_batch = time.time() - t0
##############################################################################
# Compute clustering with MiniBatchKMeans
mbk = MiniBatchKMeans(init='k-means++', n_clusters=3, batch_size=batch_size,
n_init=10, max_no_improvement=10, verbose=0)
t0 = time.time()
mbk.fit(X)
#使用MiniBatchKMeans 对 3000数据集训练算法的时间消耗
t_mini_batch = time.time() - t0
##############################################################################
# Plot result
#创建一个绘图对象, 并设置对象的宽度和高度, 如果不创建直接调用plot, Matplotlib会直接创建一个绘图对象
'''
当绘图对象中有多个轴的时候,可以通过工具栏中的Configure Subplots按钮,
交互式地调节轴之间的间距和轴与边框之间的距离。
如果希望在程序中调节的话,可以调用subplots_adjust函数,
它有left, right, bottom, top, wspace, hspace等几个关键字参数,
这些参数的值都是0到1之间的小数,它们是以绘图区域的宽高为1进行正规化之后的坐标或者长度。
'''
fig = plt.figure(figsize=(8, 3))
fig.subplots_adjust(left=0.02, right=0.98, bottom=0.05, top=0.9)
colors = ['#4EACC5', '#FF9C34', '#4E9A06']
# We want to have the same colors for the same cluster from the
# MiniBatchKMeans and the KMeans algorithm. Let's pair the cluster centers per
# closest one.
k_means_cluster_centers = np.sort(k_means.cluster_centers_, axis=0)
mbk_means_cluster_centers = np.sort(mbk.cluster_centers_, axis=0)
k_means_labels = pairwise_distances_argmin(X, k_means_cluster_centers)
mbk_means_labels = pairwise_distances_argmin(X, mbk_means_cluster_centers)
order = pairwise_distances_argmin(k_means_cluster_centers,
mbk_means_cluster_centers)
# KMeans
ax = fig.add_subplot(1, 3, 1) #add_subplot 图像分给为 一行三列,第一块
for k, col in zip(range(n_clusters), colors):
my_members = k_means_labels == k
cluster_center = k_means_cluster_centers[k]
ax.plot(X[my_members, 0], X[my_members, 1], 'w',
markerfacecolor=col, marker='.')
ax.plot(cluster_center[0], cluster_center[1], 'o', markerfacecolor=col,
markeredgecolor='k', markersize=6)
ax.set_title('KMeans')
ax.set_xticks(())
ax.set_yticks(())
plt.text(-3.5, 1.8, 'train time: %.2fs\ninertia: %f' % (
t_batch, k_means.inertia_))
# MiniBatchKMeans
ax = fig.add_subplot(1, 3, 2)#add_subplot 图像分给为 一行三列,第二块
for k, col in zip(range(n_clusters), colors):
my_members = mbk_means_labels == order[k]
cluster_center = mbk_means_cluster_centers[order[k]]
ax.plot(X[my_members, 0], X[my_members, 1], 'w',
markerfacecolor=col, marker='.')
ax.plot(cluster_center[0], cluster_center[1], 'o', markerfacecolor=col,
markeredgecolor='k', markersize=6)
ax.set_title('MiniBatchKMeans')
ax.set_xticks(())
ax.set_yticks(())
plt.text(-3.5, 1.8, 'train time: %.2fs\ninertia: %f' %
(t_mini_batch, mbk.inertia_))
# Initialise the different array to all False
different = (mbk_means_labels == 4)
ax = fig.add_subplot(1, 3, 3)#add_subplot 图像分给为 一行三列,第三块
for k in range(n_clusters):
different += ((k_means_labels == k) != (mbk_means_labels == order[k]))
identic = np.logical_not(different)
ax.plot(X[identic, 0], X[identic, 1], 'w',
markerfacecolor='#bbbbbb', marker='.')
ax.plot(X[different, 0], X[different, 1], 'w',
markerfacecolor='m', marker='.')
ax.set_title('Difference')
ax.set_xticks(())
ax.set_yticks(())
plt.show()</span>更多内容请参考官方网址:http://scikit-learn.org/dev/modules/clustering.html#clustering











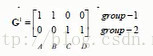















 1076
1076











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








