折线平行线的计算方法

给定一个简单多边形，多边形按照顺时针或者逆时针的数许排列

内部等距离缩小或者外部放大的多边形，实际上是由距离一系列平行已知多边形的边，并且距离为L的线段所构成的。

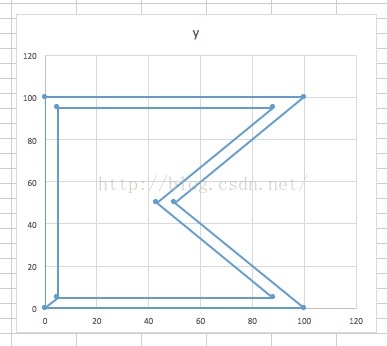
外围的是原多边形，内侧是新的多边形

算法构造

多边形的相邻两条边，L1和L2，交于Pi点

做平行于L1和L2，平行线间距是L的，并且位于多边形内部的两条边，交于Qi

我们要计算出Qi的坐标

如图，

PiQi向量，显然是等于平行四边形的两个相邻边的向量v1和v2的和的

而v1和v2向量的方向，就是组成多边形的边的方向，可以用顶点差来表示

v1和v2向量的长度是相同的，等于平行线间距L与两个线段夹角的sin值的除法。

即： Qi ＝ Pi ＋ (v1 + v2)

    Qi = Pi + L / sinθ * ( Normalize(v2) + Normalize(v1))

    Sin θ = |v1 × v2 | /|v1|/|v2|

计算步骤：

⑴、获取多边形顶点数组PList;

⑵、计算DPList[V_i+1-V_i];

⑶、单位化NormalizeDPList,得到NDP[DP_i];（用同一个数组存储）

⑷、Sinα = Dp(i+1) X DP(i);

⑸、Qi = Pi + d/sinα (NDP_i+1-NDP_i)

⑹、这样一次性可以把所有顶点计算完。

注意，交换Qi表达式当中NDP_i+1-NDP_i的顺序就可以得到外部多边形顶点数组。

用Swift实现的代码如下，在playground可直接运行

import Foundation

class Point2D  {

    var x:Double =0

    var y:Double =0

    init(_ x:Double,_ y:Double){self.x=x;self.y=y}

    init( point:Point2D){x=point.x;y=point.y}

}

//func += (inout left:Point2D, right:Point2D )     { left.x+=right.x;left.y += right.y;}

func +  (left:Point2D, right:Point2D)->Point2D   {return Point2D(left.x+right.x, left.y+right.y)}

func -  (left:Point2D, right:Point2D)->Point2D   {return Point2D(left.x-right.x, left.y-right.y)}

func *  (left:Point2D, right:Point2D)->Double    {return left.x*right.x + left.y*right.y}

func *  (left:Point2D, value:Double )->Point2D   {return Point2D(left.x*value, left.y*value)}

// 自定义的向量差乘运算符号，

infix operator ** {}

func ** (left:Point2D, right:Point2D)->Double {return left.x*right.y - left.y*right.x}

var pList   = [Point2D]()  // 原始顶点坐标， 在initPList函数当中初始化赋值

var dpList  = [Point2D]() // 边向量dpList［i＋1］－ dpLIst［i］ 在 initDPList函数当中计算后赋值

var ndpList = [Point2D]() // 单位化的边向量， 在initNDPList函数当中计算后肤质，实际使用的时候，完全可以用dpList来保存他们

var newList = [Point2D]()  // 新的折线顶点，在compute函数当中，赋值

// 初始化顶点队列

func initPList(){

    pList  = [ Point2D(0,0),

               Point2D(0,100),

               Point2D(100,100),

               Point2D(50,50),

               Point2D(100,0),

             ]

}

// 初始化dpList  两顶点间向量差

func initDPList()->Void{

    print("计算dpList")

    var index  : Int

    for index=0; index<pList.count; ++index{

        dpList.append(pList[index==pList.count-1 ? 0: index+1]-pList[index]);

        print("dpList[\(index)]=(\(dpList[index].x),\(dpList[index].y))")

    }

}

// 初始化ndpList，单位化两顶点向量差

func initNDPList()->Void{

    print("开始计算ndpList")

    var index=0;

    for ; index<dpList.count; ++index {

        ndpList.append(dpList[index] * ( 1.0 /sqrt(dpList[index]*dpList[index])));

        print("ndpList[\(index)]=(\(ndpList[index].x),\(ndpList[index].y))")

    }

}

// 计算新顶点， 注意参数为负是向内收缩， 为正是向外扩张

func computeLine(dist:Double)->Void{

    print("开始计算新顶点")

    var index = 0

    let count = pList.count;

    for ; index<count; ++index {

        var point:Point2D

        let startIndex = index==0 ? count-1 : index-1

        let endIndex   = index

        

        let sina =ndpList[startIndex] **ndpList[endIndex]

        let length = dist / sina

        let vector =ndpList[endIndex] -ndpList[startIndex]

        point = pList[index] + vector*length

        newList.append(point);

        print("newList[\(index)] = (\(point.x),\(point.y))")

    }

}

// 整个算法的调用顺序

func run()->Void {

    initPList();

    initDPList()

    initNDPList()

    computeLine(-5)  // 负数为内缩， 正数为外扩。 需要注意算法本身并没有检测内缩多少后折线会自相交，那不是本代码的示范意图

}

run()