0 预备知识
l 设离散型随机变量X的分布律为
则称 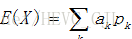
l 设连续型随机变量X的概率密度函数(PDF)为
其数学期望定义为
l 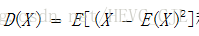
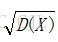
l 正态分布 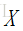
概率密度函数
l 设(X, Y)为二维随机变量,若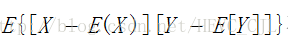
 本文介绍了高斯混合模型(GMM)及其与单高斯模型(SGM)的区别,详细阐述了GMM的参数估计过程,包括EM算法的E步和M步。同时,还讲解了K-means算法的聚类步骤和收敛条件,帮助理解两种不同的数据建模方法。
本文介绍了高斯混合模型(GMM)及其与单高斯模型(SGM)的区别,详细阐述了GMM的参数估计过程,包括EM算法的E步和M步。同时,还讲解了K-means算法的聚类步骤和收敛条件,帮助理解两种不同的数据建模方法。
l 设离散型随机变量X的分布律为
则称 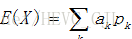
l 设连续型随机变量X的概率密度函数(PDF)为
其数学期望定义为
l 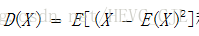
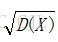
l 正态分布 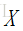
概率密度函数
l 设(X, Y)为二维随机变量,若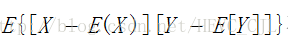

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?


