点在多边形内算法——判断一个点是否在一个复杂多边形的内部

新页面（new page）介绍了将样条曲线添加到此技术的内容。也可以访问多边形内最短路径页（shortest-path-through-polygonpage）！

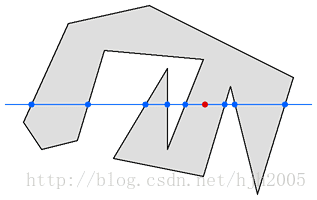
图 1

图1显示了一个具有14条边的凹多边形。我们要判断红色点是否在多边形内。

解决方案是将测试点的Y坐标与多边形的每一个点进行比较，我们会得到一个测试点所在的行与多边形边的交点的列表。在这个例子中有8条边与测试点所在的行相交，而有6条边没有相交。如果测试点的两边点的个数都是奇数个则该测试点在多边形内，否则在多边形外。在这个例子中测试点的左边有5个交点，右边有三个交点，它们都是奇数，所以点在多边形内。

（注意：这个算法适用于顺时针和逆时针绘制的多边形。）

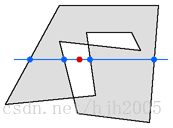
图 2

图2显示了多边形自交的情况。在这个例子中多边形的10条边有些互相交叉。这种情况很像汇编语言中的“异或”（XOR）。多边形中重叠的部分剔除。因此测试点在多边形的外面，我们从它的左右两边各有两个交点也可以看出来。

图 3

图3中多边形没有重叠，但是有两条边相交。这种情况下算法也没有问题，任然可以正常工作。

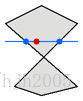
图 4

图4显示了当我们要测试的点所在的扫描行正好穿过多边形的一个顶点，因此扫描行与边a有一个交点，与边b也有一个交点，一共有两个角点，测试点的右边也是同样的情况，那按照我们的算法得到：测试点在多边形外的结论，但这显然是错误的！

要解决这种情况遇到的问题非常简单。边上的点是否与扫描行相交，我们要看边的两个端点是否是在扫描行的两侧，在扫描行上或上方的端点我们把它认为是同一种情况，那图4中边a的一个端点在扫描线的下方，另一个点在扫描线上或上方，所以边a与扫描线相交，而边b的两个端点都在扫描线上或上方，所以边b与扫描线不相交。

图 5

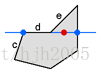
图5显示的多边形上一条边完全与扫描行重合的情况。根据图4中具体描述的边c的一个端点在扫描线的下方另一个端点在扫描线上或上方，所以边c与扫描线有一个交点，而边d的两个端点都在扫描线上或以上，所以无交点，边e也是两个端点都在扫描线上或以上，所以也没交点。

图 6

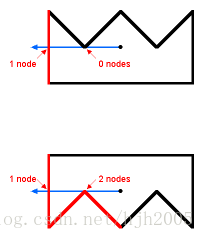
图6说明了一种特殊的情况（由加州州立理工大学的John David Munch指出）。多边形的一个角刚好落在扫描线上。其实这也没问题，上面的图中只有红色的边与扫描线相交产生交点，所以第一张图有1个交点第二张图有3个交点，交点的个数任然是奇数个，所以测试点在多边形内部。

多边形的边

如果测试点刚好在多边形的边上，则这种算法得到的结果是不确定的；例如结果可能是“在里面”或“不在里面”，这取决于很多不定的因素例如多边形在坐标系统中的方向。（不过这也没啥影响，因为多边形的边是无限小的，and points that fall right on the edge can go either way withouthurting the look of the polygon）

 

C代码例子

// Globals which should be set before calling this function:
//
// int    polySides  =  how many cornersthe polygon has
// float  polyX[]    =  horizontalcoordinates of corners
// float  polyY[]    =  verticalcoordinates of corners
// float  x,y       =  point to be tested
//
// (Globals are used in this example for purposes of speed.  Change as
// desired.)
//
//  Thefunction will return YES if the point x,y is inside the polygon, or
//  NOif it is not.  If the point is exactly on the edge of the polygon,
// then the function may return YES or NO.
//
// Note that division by zero is avoided because the division is protected
//  bythe "if" clause which surrounds it.

bool pointInPolygon() {

  int   i,j=polySides-1 ;
  bool  oddNodes=NO     ;

  for (i=0;i<polySides; i++) {
    if(polyY[i]<y && polyY[j]>=y
    ||  polyY[j]<y&& polyY[i]>=y) {
      if(polyX[i]+(y-polyY[i])/(polyY[j]-polyY[i])*(polyX[j]-polyX[i])<x) {
        oddNodes=!oddNodes;}}
    j=i;}

  returnoddNodes; }

 

下面是由Nathan Mercer提供的效力比较的的版本，蓝色的代码eliminatescalculations on sides that are entirely to the right of the test point.。虽然对某些多边形来说可能不是最快的方法，但是大多数情况下是最快的。

// Globals which should be set before calling this function:
//
// int    polySides  =  how many cornersthe polygon has
// float  polyX[]    =  horizontalcoordinates of corners
// float  polyY[]    =  verticalcoordinates of corners
// float  x,y       =  point to be tested
//
// (Globals are used in this example for purposes of speed.  Change as
// desired.)
//
//  Thefunction will return YES if the point x,y is inside the polygon, or
//  NOif it is not.  If the point is exactly on the edge of the polygon,
// then the function may return YES or NO.
//
// Note that division by zero is avoided because the division is protected
//  bythe "if" clause which surrounds it.

bool pointInPolygon() {

  int   i,j=polySides-1 ;
  bool  oddNodes=NO     ;

  for (i=0;i<polySides; i++) {
    if((polyY[i]< y && polyY[j]>=y
    ||   polyY[j]<y && polyY[i]>=y)
    &&  (polyX[i]<=x || polyX[j]<=x)){
      if(polyX[i]+(y-polyY[i])/(polyY[j]-polyY[i])*(polyX[j]-polyX[i])<x) {
        oddNodes=!oddNodes;}}
    j=i;}

  returnoddNodes; }

这里是由提供了另一个高效的版本。内部的if语句消除或替代了异或操作。

// Globals which should be set before calling this function:
//
// int    polySides  =  how many cornersthe polygon has
// float  polyX[]    =  horizontalcoordinates of corners
// float  polyY[]    =  verticalcoordinates of corners
// float  x,y       =  point to be tested
//
// (Globals are used in this example for purposes of speed.  Change as
// desired.)
//
//  Thefunction will return YES if the point x,y is inside the polygon, or
//  NOif it is not.  If the point is exactly on the edge of the polygon,
// then the function may return YES or NO.
//
// Note that division by zero is avoided because the division is protected
//  bythe "if" clause which surrounds it.

bool pointInPolygon() {

  int   i,j=polySides-1 ;
  bool  oddNodes=NO     ;

  for (i=0;i<polySides; i++) {
    if((polyY[i]< y && polyY[j]>=y
    ||   polyY[j]<y && polyY[i]>=y)
    && (polyX[i]<=x || polyX[j]<=x)) {
      oddNodes^=(polyX[i]+(y-polyY[i])/(polyY[j]-polyY[i])*(polyX[j]-polyX[i])<x);}
    j=i;}

  returnoddNodes; }

 

整型问题

假如你试图画一个像下图中蓝色的多边形，但是出来的却是有横线和竖线组成的边的多边形，如下图中的红色的多边形。出现这种情况可能是将多边形的顶点坐标变量定义成了整型而非浮点型，仔细地检查你的代码确保多边形的顶点是以浮点型定义且传递的。

图 7