判断点是否在多边形内的算法

如果判断点是否在凸多边形内，则有多种方法，方法简单，计算速度也快，直接使用物理引擎做判断也行

但实际问题中遇到的多边形不一定是凸多边形,它可能是凹边行或者复合多边形

判断一个点在多边形内或多边形外，射线法是个不错的选择

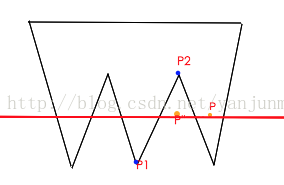
射线法，判断一点是否在多边形内或多边形外，只要从这点起，作一条射线，例如，沿x向直到负无穷，如果越过的边数是单数，这点就在多边形内，越过的边数是偶数，这点就在多边形外。

如图

注意到如果从P作水平向左的射线的话，如果P在多边形内部，那么这条射线与多边形的交点必为奇数，如果P在多边形外部，则交点个数必为偶数（0也在内）。所以，我们可以顺序考虑多边形的每条边，求出交点的总个数。还有一些特殊情况要考虑。假如考虑边(P1,P2)，
1)如果射线正好穿过P1或者P2,那么这个交点会被算作2次，处理办法是如果P的从坐标与P1,P2中较小的纵坐标相同，则直接忽略这种情况
2)如果射线水平，则射线要么与其无交点，要么有无数个，这种情况也直接忽略。
3)如果射线竖直，而P0的横坐标小于P1,P2的横坐标，则必然相交。

4)再判断相交之前，先判断P是否在边(P1,P2)的上面，如果在，则直接得出结论：P再多边形内部

计算X轴坐标

//计算交点逻辑

tanα = b /  c;

tanα = d / a;

d = b*a / c;

代码：

bool HelloWorld::IsPointInsideShape(Vec2 pos,std::vector<Vec2>& m_vAllShape)
{
    int nCross = 0;
    int nCount = (int)m_vAllShape.size();
    Vec2 p = pos;
    for (int i = 0; i < nCount; i++)
    {
        Vec2 p1 = m_vAllShape[i];
        Vec2 p2 = m_vAllShape[(i + 1) % nCount];
        // 求解 y=p.y 与 p1p2 的交点
        if (p1.y == p2.y)
        {// p1p2 与 y=p0.y平行
            continue;
        }
        if (p.y < MIN(p1.y, p2.y))
        {// 交点在p1p2延长线上
            continue;
        }
        if (p.y >= MAX(p1.y, p2.y))
        {// 交点在p1p2延长线上
            continue;
        }
        // 求交点的 X 坐标 --------------------------------------------------------------
        double x = (double)(p.y - p1.y) * (double)(p2.x - p1.x) / (double)(p2.y - p1.y) + p1.x;
        if (x > p.x){
            nCross++; // 只统计单边交点
        }
    }
    // 单边交点为偶数，点在多边形之外
//    if (nCross % 2 == 1) {
//        log("在多边形内");
//    }
//    if (nCross % 2 == 0) {
//        log("在多边形外");
//    }
    return (nCross % 2 == 1);
}