对称加密与公钥加密(下)

在本篇博文中，我将讲解公钥密码以及公钥密码与对称称密码的比较

一.公钥密码

1、什么是公钥密码

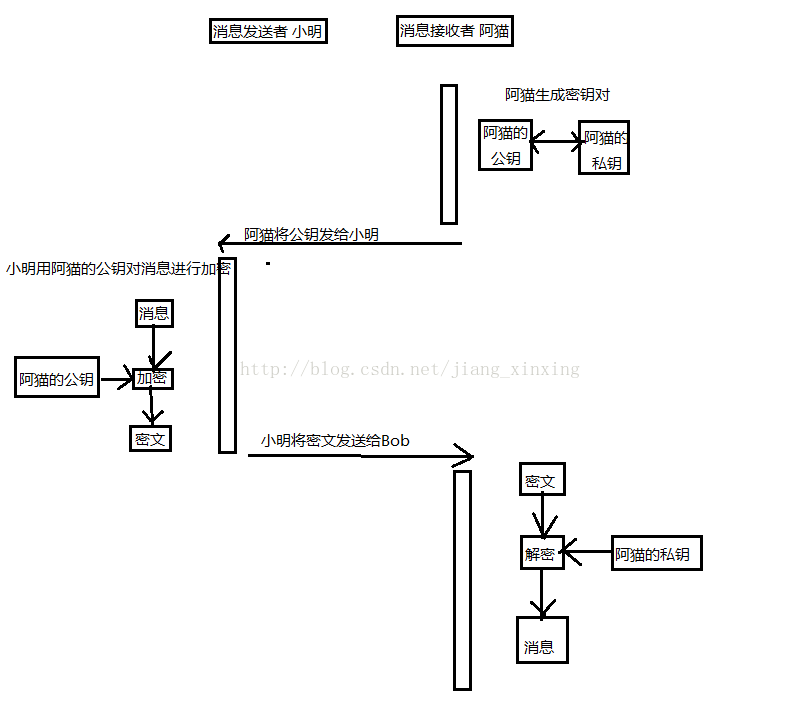
公钥密码这种，密钥分为两种，加密密钥与解密密钥，发送用加密密钥对消息进行加密，接收者用解密密钥对密文进行解密。一般情况下，加密密钥是公开的，称为公钥，解密密钥是非公开的，称为私钥。公钥与私钥是一一对应的。

这样，阿狗可能拥有阿猫的公钥，但公钥并不是解密的密钥，故而阿狗无法完成解密操作

2.公钥密码存在的问题

公钥密码解决了密钥配送问题，但并不意味着它能解决所有的问题，因为我们要判断所得到的公钥是否正确合法，这个问题被称为公钥认证问题。这个问题这里我并不打算解决，若想知道答案，最好的方法是关注下面的博客

此外，公钥密码还有一个问题就是，它的处理速度只有对称密码的几百分之一，关于这个问题，，关注博客吧，下一篇博客会讲。

3.RSA

RSA是一种广泛使用的公钥密码，可以被用于公钥密码和数字签名

3.1.RSA加密
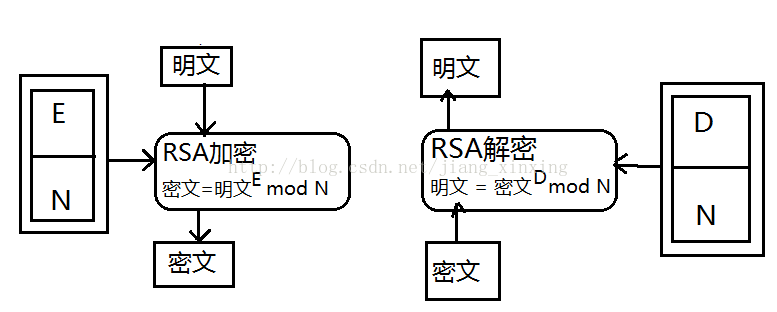
在RSA中，明文、密钥、密文，RSA可以用下面这个公式来加密

E和N是RSA的加密密钥，也就是说，E和N组合就是公钥，一般会写成“公钥是(E, N)或者“公钥{(E, N}”

3.2.RSA的解密

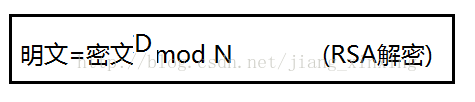
RSA的解密和加密一样简单，也是一个公式

D和N的组合是私钥，只有知道D和N两个数组合起来才能够完成解密运算

3.3生成密钥对
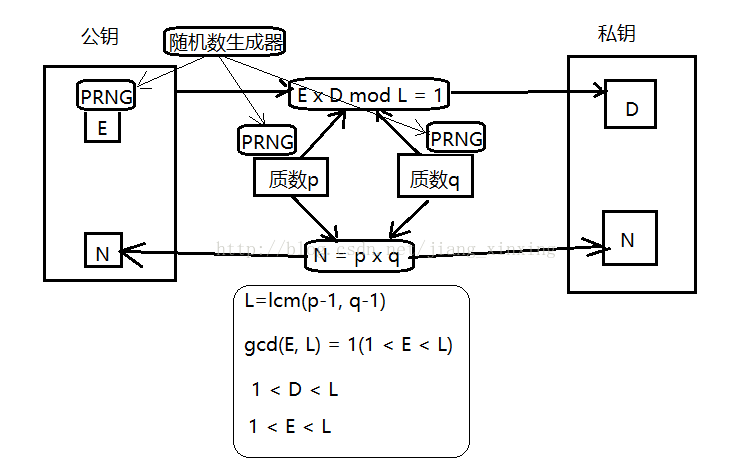
E和N是公钥，D和N是私钥，因此求E、D和N这三个数就是生成密钥。RSA密钥生成步骤如下
(1).求N
(2).求L
(3).求E
(4).求D

(1).求N
a.准备两个很大的质数p和q (用伪随机数生成器生成)
b.N = p x q (p和q为质数)

(2).求L
L=lcm(p-1, q-1) (L是p-1和q-1的最小公倍数)

(3).求E
gcd(E, L) = 1(1 < E < L)    E和L的最大公约数必须为1(E和L互质)
到目前为止我们已经求出E和N,也就是说我们已经生成密钥中的公钥

(4).求D
数D是由数E计算得到的。D、E和L必须具备以下关系
1 < D < L
E x D mod L = 1
到此为止我们也可以生成私钥啦。整个过程如下图

4.对RSA的攻击
咱们先来整理一下攻击者知道那些信息，不知道那些信息
【攻击者知道的信息】
密文:可以通过窃听来获取
数字E和N:公开的信息，因此破译者知道E和N
【密码破译者不知道的信息】
明文:需要破译的内容
数字D:私钥中至少D是不知道的东西
其他:p、q和L
破解方式一
暴力破解D:D的长度足够长的话，想找D的值难度很大，这种方法不现实。
破解方式二
通过E和N求出D:E x D mod L = 1; L = lcm(p-1, q-1),p和q无法知道，N=p x q，可以对N做质因数分解，但是如果N是大整数，现在还没有很好的算法，这种方法不现实；但如果质因数分解求q和p，恭喜你，你已经破解RSA啦
破解方式三
通过推测p和q:这还是有可能的，如果推测出来，也恭喜你，你已经破解RSA啦

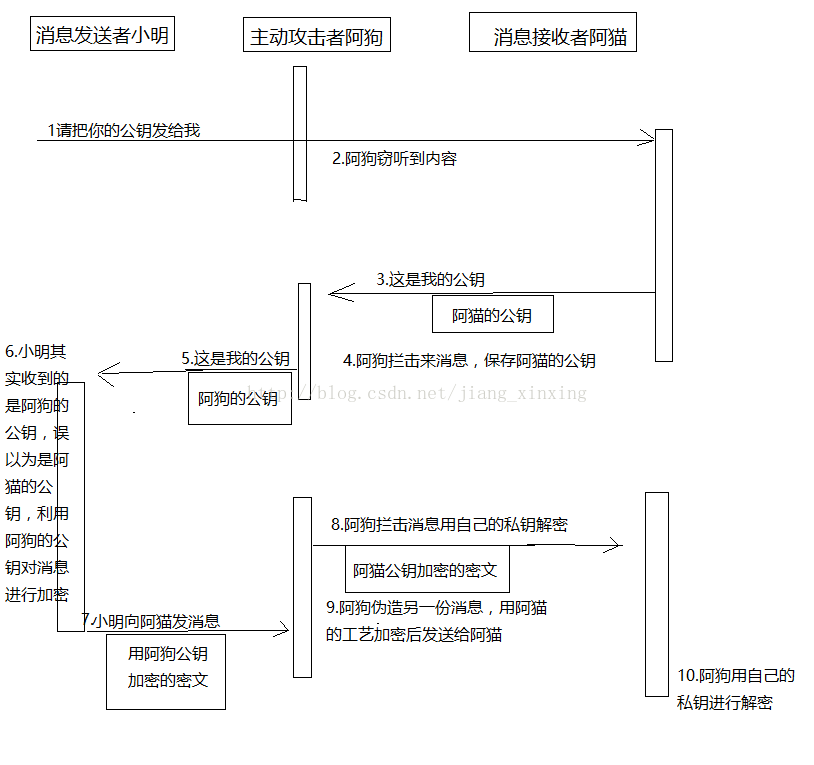
5.中间人攻击
这种方法虽然不能破解RSA,但却是一种针对机密性的有效攻击，看下图你就明白

6.选择密文攻击
选择密文攻击一般是通过提示信息去尝试解密，使用RSA-OAEP，RSA-OAEP会在加密明文前生成一些认证信息，包括明文的散列值和一定数量的0，然后再对填充后的明文用RSA加密。这样攻击者就无法得到解密提示的相关信息

7.其他公钥密码
(1)ElGamal方式
(2)Rabin方式
(3)椭圆曲线密码