今天做了一道网易的笔试题——数列还原。里面用到了全排列的想法,因此学习并总结了一下全排列算法。
1、全排列问题描述
输入一个字符串或者序列,打印出该字符串或序列中字符或元素的所有排列。例如输入字符串abc,则输出由字符a,b,c所能排列出来的所有字符串abc,acb,bac,bca,cab和cba。
2、解决思路
查了一些资料,很多都是利用递归的思想解决的。递归算法有以下几个特点:
- 必须有可达到的终止条件,否则程序陷入死循环
- 子问题在规模上比原问题小
- 子问题可通过再次递归调用求解
- 子问题的解应能组合成整个问题的解
对于字符串全排列问题,如果能生成n-1个元素的全排列,就能生成n个元素的全排列。对于只有一个元素的集合,可以直接生成全排列。所以全排列的递归终止条件很明确:只有一个元素时。我们可以分析一下全排列的过程:
(1)首先,我们固定第一个字符a,求后面两个字符bc的排列;
(2)当两个字符bc排列求好之后,我们把第一个字符a和后面的b交换,得到bac,接着我们固定第一个字符b,求后面两个字符ac的排列;
(3)现在是把c放在第一个位置的时候了,但是记住前面我们已经把原先的第一个字符a和后面的b做了交换,为了保证这次c仍是和原先处在第一个位置的a交换,我们在拿c和第一个字符交换之前,先要把b和a交换回来。在交换b和a之后,再拿c和处于第一位置的a进行交换,得到cba。我们再次固定第一个字符c,求后面两个字符b、a的排列;
(4)既然我们已经知道怎么求三个字符的排列,那么固定第一个字符之后求后面两个字符的排列,就是典型的递归思路了。
可以根据下面这张图来理解递归的过程:
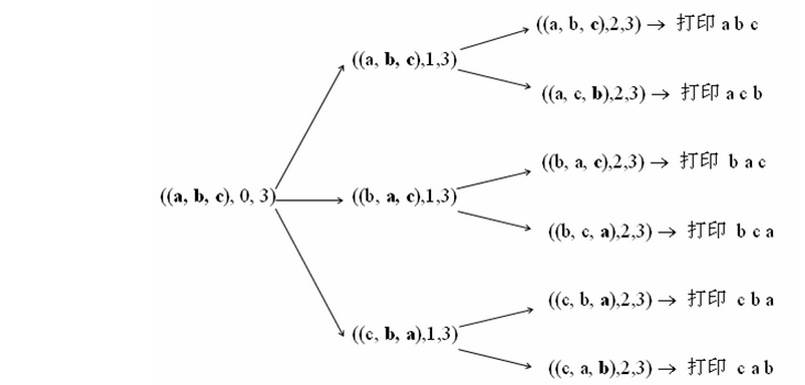
3、编程实现
程序1:字符串实现
#include<iostream>
#include<string>
#include<vector>
using namespace std;
void Permutation(string *s,int len)
{
if(len == (*s).length())
cout<<(*s)<<endl;
else
{
for(int i = len;i<(*s).length();++i)
{
swap((*s)[len],(*s)[i]);
Permutation(s,len+1);
swap((*s)[len],(*s)[i]);
}
}
}
int main()
{
string s;
cin>>s;
Permutation(&s,0);
return 0;
}
#include<iostream>
using namespace std;
void Permutation(char* pStr, char* pBegin)
{
if(*pBegin == '\0')
printf("%s\n",pStr);
else
{
for(char* pCh = pBegin; *pCh != '\0'; pCh++)
{
swap(*pBegin,*pCh);
Permutation(pStr, pBegin+1);
swap(*pBegin,*pCh);
}
}
}
int main()
{
char str[] = "abc";
Permutation(str,str);
return 0;
} #include<iostream>
#include<vector>
using namespace std;
bool find(vector<int> v,int n) //查询v中是否存在整数n
{
for(int i = 0;i<v.size();++i)
if(v[i]==n)
return true;
return false;
}
vector<vector<int>> pv; //全局变量
void Perm(vector<int> &v,int st) //对v中的数字进行全排列
{
if(st == v.size())
pv.push_back(v);
else
{
for(int i = st;i<v.size();++i)
{
swap(v[i],v[st]);
Perm(v,st+1);
swap(v[i],v[st]);
}
}
}
void change(vector<int> &v,vector<int> subv,vector<int> vpos)//将v中的0用全排之后的数字分别代替
{
for(int i = 0;i<vpos.size();++i)
v[vpos[i]] = subv[i];
}
int cal(vector<int> v) //计算顺序对的个数
{
int cnt = 0;
for(int i = 0;i<v.size()-1;++i)
for(int j = i+1;j<v.size();++j)
if(v[i]<v[j])
++cnt;
return cnt;
}
int main()
{
int n,k,tmp;
while(cin>>n>>k)
{
vector<int> v,subv,vpos;
for(int i = 0;i<n;++i)
{
cin>>tmp;
v.push_back(tmp);
}
for(int i = 0;i<v.size();++i)
if(v[i]==0)
vpos.push_back(i); //记录下vector<int>中0的位置
for(int i = 1;i<=n;++i)
if(!find(v,i))
subv.push_back(i);
Perm(subv,0);
vector<int> vcnt;
for(int i = 0;i<pv.size();++i)
{
change(v,pv[i],vpos);
vcnt.push_back(cal(v));
}
int vcntk = 0;
for(int i = 0;i<vcnt.size();++i)
if(vcnt[i]==k)
++vcntk;
cout<<vcntk<<endl;
}
return 0;
}4、含重复元素的全排列
上述思路解法有个缺陷:对于有重复元素的全排列,排列结果会有重复。这里直接给出全排列中去掉重复的规则:去重的全排列就是从第一个数字起,每个数分别与它后面非重复出现的数字交换。
上述第一段代码核心部分修正如下:
bool cmp(string s,int len,int i)
{
for(int ii = len;ii<i;++ii)
if(s[ii]==s[i])
return true;
return false;
}
void Permutation(string *s,int len)
{
if(len == (*s).length())
cout<<(*s)<<endl;
else
{
for(int i = len;i<(*s).length();++i)
{
if(!cmp(*s,len,i))
{
swap((*s)[len],(*s)[i]);
Permutation(s,len+1);
swap((*s)[len],(*s)[i]);
}
}
}
}此外全排列问题还有非递归的实现以及利用STL中的next_permutation()函数,具体见参考资料第一篇博客。
参考资料:
























 237
237

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








