傅里叶变换就是将满足一定条件的某个函数表示成三角函数(正弦/余弦)或其积分的线性组合。傅里叶变换可以看出一种工具,将一个连续的信号(不方便处理)转换成一个个小信号的叠加(好处理)。就是将信号完成从时域表示到频域表示。信号本质没有变,转换后有助于后续处理。来看一个图,原图1-4及代码转自http://fashionxu.bokee.com/4632908.html ,第5个图是我加的。
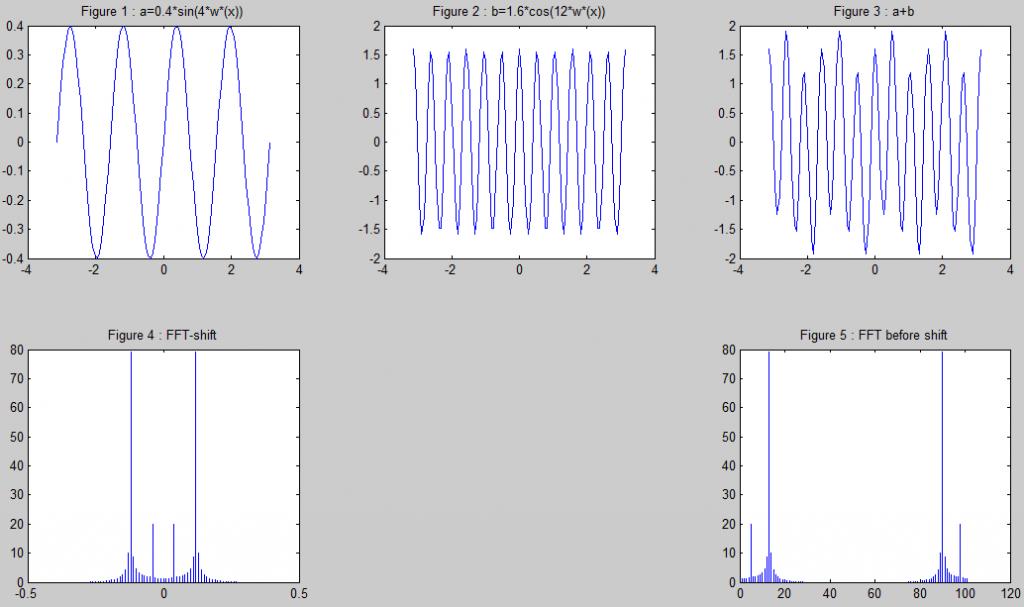
图3是由图1和图2两个三角函数波合成的,但是在时域表示下,很难对图3进行分析,于是,对图3执行傅里叶变换,转换到频域表示,如图5,就很明显。又但是,因为MATLAB FFT函数直接转换出来的数据与频率坐标是不对应的,所以用ffshift函数将零频点移到频谱中间,如图4,这样方便观看。图5的横坐标表示频率,纵坐标表示幅值。不看负频部分,从正频部分来看,里0点近的表示频率小,幅值小,对应图1中的a;离0点远的表示频率大,幅值大,对应图2中的b(请自动忽略图5的横坐标)。
PS:在信号在时域无限(一直连续)的情况下,图5应该是2高2低的4条谱线;但由于时域是有限的,所以存在一些其他频率的点。
再PS:关于如何








 傅里叶变换是将连续信号转化为正弦/余弦函数组合的过程,便于分析和处理。它将信号从时域转换到频域,帮助解析复杂信号的组成。通过MATLAB的FFT函数,可以观察到信号的频域表示,其中相位和幅度揭示了信号的特征。在图像处理中,FFTShift有助于将低频部分移至中心,便于观察。傅里叶变换在电信和信号处理等领域有广泛应用。
傅里叶变换是将连续信号转化为正弦/余弦函数组合的过程,便于分析和处理。它将信号从时域转换到频域,帮助解析复杂信号的组成。通过MATLAB的FFT函数,可以观察到信号的频域表示,其中相位和幅度揭示了信号的特征。在图像处理中,FFTShift有助于将低频部分移至中心,便于观察。傅里叶变换在电信和信号处理等领域有广泛应用。
 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章

















 5136
5136

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








