支持向量机(Support Vector Machine,SVM),可以完成对数据的分类,包括线性可分情况和线性不可分情况。
1、线性可分
首先,对于SVM来说,它用于二分类问题,也就是通过寻找一个分类线(二维是直线,三维是平面,多维是超平面)可以将数据分为两类。 并用线性函数f(x)=w·x +b来构造这个分类器(如下图是一个二维分类线)
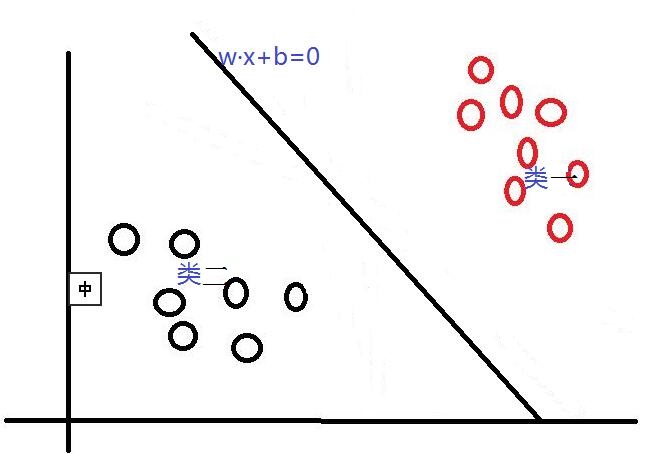
其中,w是权重向量,x为训练元组(X=(x1,x2…xn),n为特征个数,xi为每个X在属性i上对应的值),b为偏置,w·x是w和x的点积。当某数据被分类时,就会代入此函数,通过计算f(x)的值来确定所属的类别,当f(x)>0时,此数据被分为类一,当f(x)<0时,此数据被分为类二。通过观察,我们可以发现,如果我们平移或者旋转一下此分类线,同样可以完成数据的分类(如下图),那么,选择哪一个分类线才是最好的呢?

对于这个问题,SVM是通过搜索“最大边缘距离分类线”(面)来解决的。那么,什么是边缘距离,为什么要寻找最大的边缘距离呢?如下图所示,如果我们将某一分类线向右平移,在平移到右侧最大限度,又能确保此时的这个被平移的线仍然能将数据分为两类时,也就是如下图(线一)所示的:右侧与类一中某个或某些数据(实心点)相交的位置。此时正好,在线右侧和线上的数据是类一,在线左侧的数据是类二;同理,如果我们将这个分类线向左移动,也是移动到左侧最大限度(如下图线二),此时这条线刚好也与类二中的某个或某些(实心点)数据相交,线上和线左侧的数据是类二,线右侧的数据是类一。对于这两条“极限边界线”,我们可以称之为支持线,或者对于面来说,就是支持面,而确定这些支持面或者支持线的那些数据点,我们称之为支持向量。两个支持线或支持面之间的这个距离,就是我们所说的边缘距离。
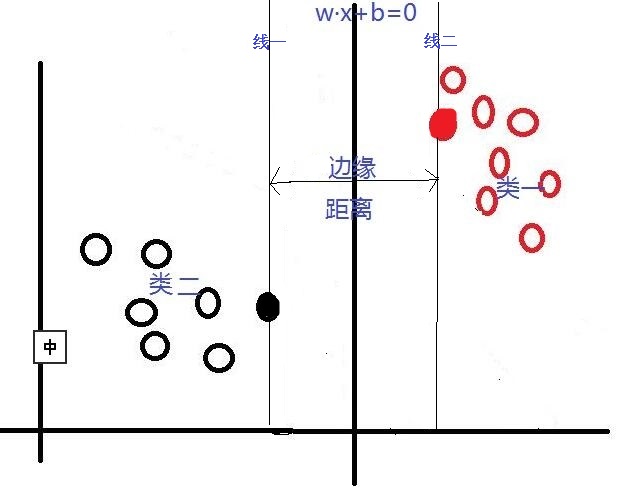
在这里我们可以发现,不同的分类线(面)会对应不同的支持线(面),支持线(面)之间的边缘距离也是不同的,并且,我们认为:边缘距离越大的分类线,对分类精度更有保证,所以,我们要找的”最好的“分类线(面),就是拥有最大边缘距离的那个分类线(面)。也就是说:对于线性可分的情况,SVM会选择最大化两类之间边缘距离的那个分类线(面)来完成二分类问题。并且此分类线(面)平行于两个支持线(面),平分边缘距离。下图是一个与上图相比,拥有更大边缘距离的分类线(面)。
2、线性不可分
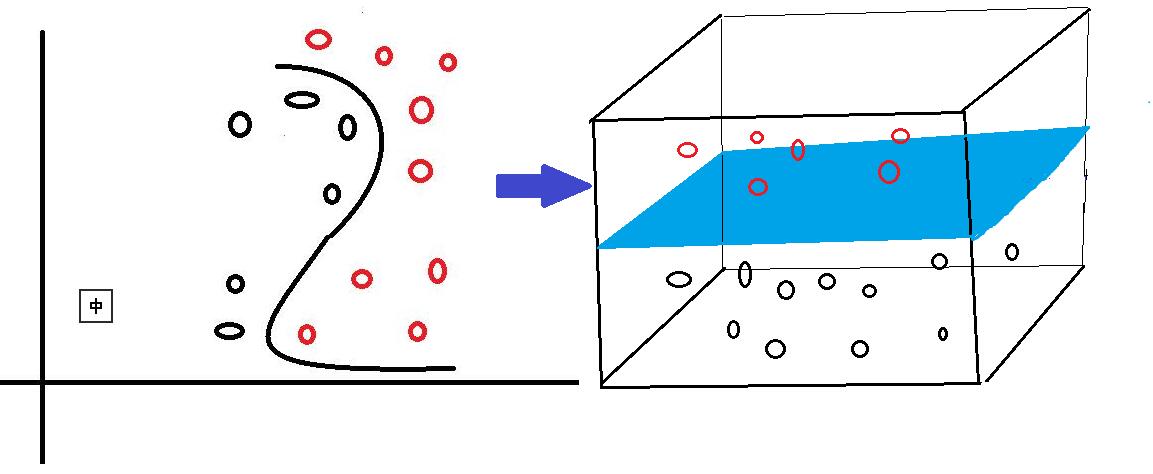
对于线性可分的情况,我们上面说到,可以通过一个线性函数f(x)=w·x +b来构造一个分类器,寻找一个有着最大边缘距离的分类线(面)来完成对数据的分类。但是,我们还会遇到另一个问题,就是,如果数据是线性不可分的情况,用一个二维直线,三维平面或者多维超平面不能完成二分类,又该如何呢?对于线性不可分问题,SVM采取的方法是将这些线性不可分的原数据向高维空间转化,使其变得线性可分。就像下图所示,对于一些数据,他们是线性不可分的,那么,通过将他们向高维转化,也许就像图中所示,将二维数据转化到三维,就可以通过一个分类面将这些数据分为两类。所以说,SVM通过将线性不可分的数据映射到高维,使其能够线性可分,再应用线性可分情况的方法完成分类。
而在这个高维转化过程中,SVM实际上并没有真正的进行高维映射,而是通过一种技巧来找出这个最大边缘分类面,即将一个叫做核函数的函数,应用于原输入数据上。这个技巧首先允许我们不需要知道映射函数是什么,只将选定的核函数应用到原输入数据上就行;其次,所有的计算都在原来的低维输入数据空间进行,避免了高维运算。对于这个核函数,可选项有好几种,包括多项式核函数,高斯径向基函数核函数,S型核函数等等。
下面写了两个matlab程序,来简单的看了一下matlab自带的SVM分类器的分类效果。在这里主要应用两个函数来完成而分类问题:
(1)svmtrain函数,其是一个训练分类模型的函数:SVMStruct = svmtrain(Training,Group,Name,Value),其输入参数为(训练数据,训练数据相应组属性,可选参数名,可选参数的值),输出为一个结构体。
可选参数有很多,包括boxconstraint,kernel_function,kernelcachelimit,kktviolationlevel,method,kktviolationlevel,mlp_params,options,polyorder,rbf_sigma,showplot,tolkkt,这里我介绍一下我下面例子中要用到的两个可选输入参数:
1、kernel_function(核函数类型):可选的核函数有linear,quadratic,polynomial,rbf,mlp,@kfun ,如果不设置核函数类型,那么默认的选用线性核函数linear。
2、showplot(绘图):是一个布尔值,用来指示是否绘制分类数据(这里是训练数据)和分类线。但是这个绘图功能只支持绘制有两个特征值的数据,也就是二维的点数据。(默认为false),在svmtrain函数中,如果将showplot设置为true,程序会自动在figure中用不同的颜色绘制出训练数据中两个类的点以及通过训练数据获得的分类线,并标注出哪些点是支持向量。(如下图是一组训练数据在通过svmtrain函数训练后,应用showplot绘制出的图形,其中,红色的+代表训练集类1中的数据,绿色的星号代表训练集类2中的数据。支持向量被O圈起。)

3、boxconstraint
svmtrain函数输出的结构体中包含训练出的分类器的信息,包括支持向量机,偏置b的值等等。
(2)svmclassify函数,其实一个应用训练的分类模型和测试数据进行分类测试的函数:Group = svmclassify(SVMStruct,Sample,’Showplot’,true),其最多只有这四个输入参数,包括(训练出的分类模型结构体,测试数据,绘图显示,’true’)。在svmclassify函数中用Showplot绘图,会绘制出svmclassify函数中输入的测试数据点,如下图所示,粉色的+为被分到类1中的测试数据,蓝色星号是被分到类2中的测试数据)
对于svmclassify函数的输出Group,其是一个n*1的数组,里面的n为测试数据个数,数组中每个元素记录的是对应顺序下的测试数据被分类后的类属性。
测试1代码:
function [ classification ] = SVM_L( train,test )
% 进行SVM线性可分的二分类处理
% 1、首先需要一组训练数据train,并且已知训练数据的类别属性,在这里,属性只有两类,并用1,2来表示。
% 2、通过svmtrain(只能处理2分类问题)函数,来进行分类器的训练
% 3、通过svmclassify函数,根据训练后获得的模型svm_struct,来对测试数据test进行分类
train=[0 0;2 4;3 3;3 4;4 2;4 4;4 3;5 3;6 2;7 1;2 9;3 8;4 6;4 7;5 6;5 8;6 6;7 4;8 4;10 10]; %训练数据点
group=[1,1,1,1,1,1,1,1,1,1,2,2,2,2,2,2,2,2,2,2]'; %训练数据已知分类情况
%与train顺序对应
test=[3 2;4 8;6 5;7 6;2 5;5 2]; %测试数据
%训练分类模型
svmModel = svmtrain(train,group,'kernel_function','linear','showplot',true);
%分类测试
classification=svmclassify(svmModel,test,'Showplot',true);
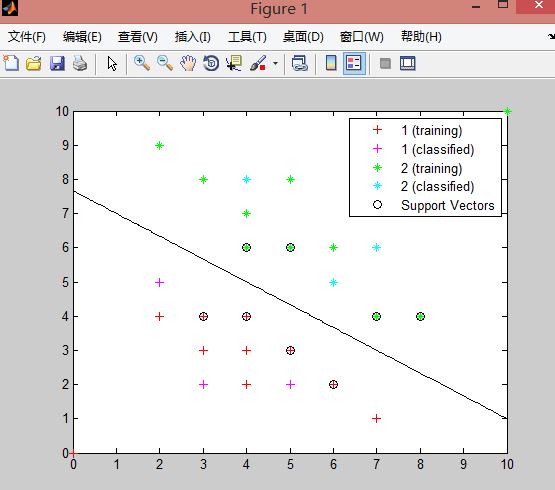
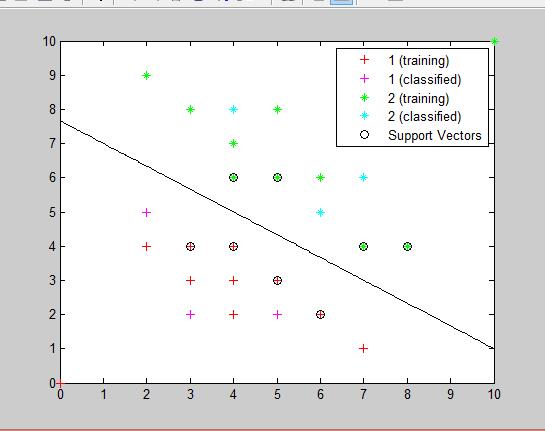
end线性可分实验结果如下图,输出的测试数据分类情况为(1 2 2 2 1 1),全部正确
测试2代码:
function [ classfication ] = SVM_NL( train,tast )
%SVM对线性不可分的数据进行处理
%在选择核函数时,尝试用linear以外的rbf,quadratic,polynomial等,观察获得的分类情况
%训练数据
train=[5 5;6 4;5 6;5 4;4 5;8 5;8 8;4 5;5 7;7 8;1 2;1 4;4 2;5 1.5;7 3;10 4;4 9;2 8;8 9;8 10];
%训练数据分类情况
group=[1,1,1,1,1,1,1,1,1,1,2,2,2,2,2,2,2,2,2,2];
%测试数据
test=[6 6;5.5 5.5;7 6;12 14;7 11;2 2;9 9;8 2;2 6;5 10;4 7;7 4];
%训练分类模型
svmModel = svmtrain(train,group,'kernel_function','rbf','showplot',true);
%分类
classification=svmclassify(svmModel,test,'Showplot',true);
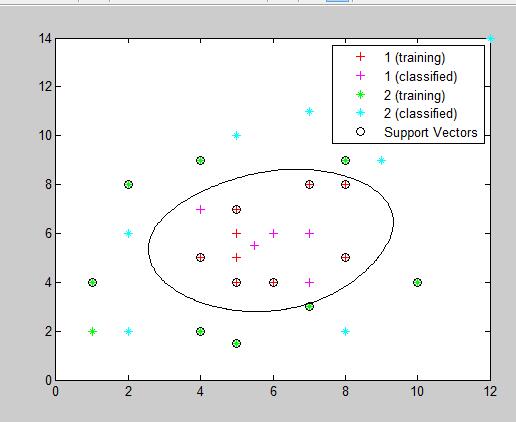
end线性不可分(使用rbf核函数)的实验结果如下图,输出的测试数据分类情况为(1 1 1 2 2 2 2 2 2 1 1),全部正确
因为实验数据是二维的(有两个特征值),可以通过Showplot显示出数据点的分类情况以及最大边界分类线,,且实验数据间干扰较小,分类效果很好。下面的实验将选用matlab提供的一组分类数据来测试一下特征数量对实验精度的影响
测试3代码:
function [ classfication ] = SVM2_2( train,test )
%使用matlab自带的关于花的数据进行二分类实验(150*4),其中,每一行代表一朵花,
%共有150行(朵),每一朵包含4个属性值(特征),即4列。且每1-50,51-100,101-150行的数据为同一类,分别为setosa青风藤类,versicolor云芝类,virginica锦葵类
%实验中为了使用svmtrain(只处理二分类问题)因此,将数据分为两类,51-100为一类,1-50和101-150共为一类
%实验先选用2个特征值,再选用全部四个特征值来进行训练模型,最后比较特征数不同的情况下分类精度的情况。
load fisheriris %下载数据包含:meas(150*4花特征数据)
%和species(150*1 花的类属性数据)
meas=meas(:,1:2); %选取出数据前100行,前2列
train=[(meas(51:90,:));(meas(101:140,:))]; %选取数据中每类对应的前40个作为训练数据
test=[(meas(91:100,:));(meas(141:150,:))];%选取数据中每类对应的后10个作为测试数据
group=[(species(51:90));(species(101:140))];%选取类别标识前40个数据作为训练数据
%使用训练数据,进行SVM模型训练
svmModel = svmtrain(train,group,'kernel_function','rbf','showplot',true);
%使用测试数据,测试分类效果
classfication = svmclassify(svmModel,test,'showplot',true);
%正确的分类情况为groupTest,实验测试获得的分类情况为classfication
groupTest=[(species(91:100));(species(141:150))];
%计算分类精度
count=0;
for i=(1:20)
if strcmp(classfication(i),groupTest(i))
count=count+1;
end
end
fprintf('分类精度为:%f\n' ,count/20);
end选取数据中前两个特征值,进行实验获得的实验精度为0.80,如下图:
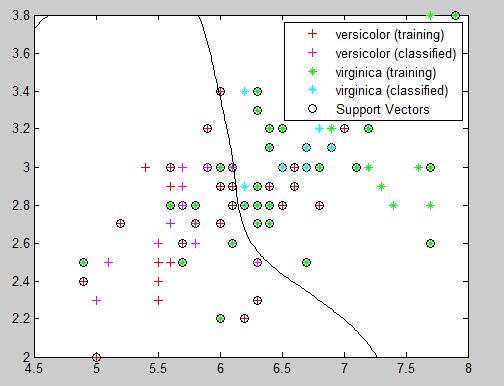
将上面实验3中的代码”meas=meas(:,1:2); “改为“meas=meas(:,1:4);” 也就是选取了全部四个特征值,此时的分类结果不能再用showplot打印出,但是,获得的分类精度为1.0 ,这说明,选择适当的特征数量,对分类模型的准确度是有很大影响的。





 本文详细介绍了支持向量机(SVM)的工作原理及其在不同数据集上的应用。涵盖了线性可分与线性不可分两种情况下的分类方法,并通过Matlab程序演示了SVM在实际数据集上的分类效果。
本文详细介绍了支持向量机(SVM)的工作原理及其在不同数据集上的应用。涵盖了线性可分与线性不可分两种情况下的分类方法,并通过Matlab程序演示了SVM在实际数据集上的分类效果。

















 2656
2656

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








