机器学习：主题模型：PLSA

http://blog.csdn.net/pipisorry/article/details/42560877
* 概率潜在语义分析简称pLSA(Probabilisticlatent semantic analysis)
* 概率潜在语义分析与标准潜在语义分析的不同是，标准潜在语义分析是以共现表（就是共现的矩阵）的奇异值分解的形式表现的，而概率潜在语义分析却是基于派生自LCM的混合矩阵分解。考虑到word和doc共现形式，概率潜在语义分析基于多项式分布和条件分布的混合来建模共现的概率。所谓共现其实就是W和D的一个矩阵，所谓双模式就是在W和D上同时进行考虑。基于概率统计的PLSA模型，用EM算法学习模型参数。

---

PLSA的推导

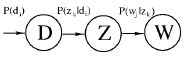
• D是文档；Z代表主题；W代表观察到的单词
• $p(d_i)$ 是单词出现的在文档$d_i$ 的概率
• $p(z_k|d_i)$ 是文档$d_i$中出现主题$z_k$的概率
• $p(w_j|z_k)$是给定主题词$z_k$出现单词 $w_j$的概率
  （每个主题在所有词项上服从Multinomial分布，每个文档在所有文档上服从Multinomial分布）
• 文档的生成过程：
  
  1. 以$p(d_i)$的概率选择文档$d_i$
  2. 以$p(z_k|d_i)$的概率选择主题
  3. 以$p(w_j|z_k)$的概率产生一个单词

观察到的数据是：$(d_j,w_j)$

$p(d_i,w_j) = p(d_i)d(w_j|d_i)$
$p(w_j|d_i)=\sum_{k=1}^K p(w_j|z_k)p(z_k|d_i)$

其中：$p(z_k|d_i)和p(w_j|z_k)$分别对应了两组Multinomial分布，需要去估计参数

---

PLSA的EM算法估计参数

• 需要去估计的参数是：$p(z_k|d_i)，p(w_j|z_k)$

直接使用MLE估算参数

$L = \prod_{i=1}^N \prod_{j=1}^M p(d_i,w_j)$
$=\prod_{i} \prod_j p(d_i,w_j)^{n(d_i,w_j)}$ ……..$(n(d_i,w_j))$是单词 $w_j$出现在文档$d_i$的次数
$l=\sum_{i=1}^N\sum_{j=1}^M n(d_i,w_j) logp(d_i,w_j)$
$=\sum_i\sum_j n(d_i,w_j) logp(d_i,w_j)$
$=\sum_i\sum_j n(d_i,w_j)logp(w_j|d_i)p(d_i)$
$=\sum_i\sum_j n(d_i,w_j) log(\sum_{k=1}^Kp(w_j|z_k)p(z_k|d_j)p(d_i))$

上式是关于$p(z_k|d_i)和p(w_j|z_k)$的函数；对于上述包括隐变量或者是缺失数据的公式采用EM算法

EM算法求解步骤

PLSA中，incomplete data是观察到的$(d_i,w_j)$，隐含主题是$z_k$，完整的数据是$(d_j, w_j, z_k)$

(1)E步骤：求含隐变量Givern当前估计的参数条件下的后验概率。
(2)M步骤：最大化Complete data对数似然函数的期望，此时使用E步骤计算隐含变量的后验概率，得到新的参数
两部迭代直到收敛

• E步骤：假设 $p(z_k|d_j), p(w_j|z_k)$已知,初始化时随机赋值

$p(z_k|d_i,w_j)=\frac{p(w_j|z_k)p(z_k|d_i)}{\sum_{l=1}^kp(w_j|z_l)p(z_l|d_i)}$

• M步骤：最大化 Complete data对数似然函数的期望

$l = \sum_i \sum_j n(d_i,w_j)$
$= \sum_i \sum_j n(d_i,w_j) log(p(w_j|d_i)p(d_i))$
$=\sum_i \sum_j n(d_i,w_j)(log p(w_j|d_i)+logp(d_i))$
$=(\sum_i\sum_j n(d_i,w_j)log p(w_j|d_i))+(\sum_i \sum_j n(d_i,w+j)logp(d_i))$
=>
$l_{new} = (\sum_i\sum_j n(d_i,w_j)log p(w_j|d_i))$
$E(l_{new}=\sum_i \sum_j n(d_i,w_j) \sum_{k=1}^K p(z_k|d_i,w_j) log p(w_j,z_k|d_i)$
$=\sum_i\sum_j n(d_i,w_j)\sum_{k=1}^K p(z_k|d_i,w_j)log p(w_j,z_k)p(z_k,d_i)$

---

目标函数的建立

关于参数$p(z_k|d_i), p(w_j|z_k)$的函数E，且其约束：
$\sum_{j=1}^Mp(w_j|z_k) =1$
$\sum_{k=1}^K p(z_k|d_i) =1$

$E=\sum_i\sum_j n(d_i,w_j)\sum_{k=1}^K p(z_k|d_i,w_j)log p(w_j,z_k)p(z_k,d_i)$

转换为：求等式约束的极值。

---

结论

M步:

$p(w_j|z_k) = \frac{\sum_i n(d_i,w_j)p(z_k|d_i,w_j)}{\sum_{m=1}^M n(d_i,w_j)p(z_k|d_i,w_j)}$

$p(z_k|d_i) = \frac{\sum_j n(d_i,w_j)p(z_k|d_i,w_j)}{\sum_{k=1}^K \sum_j n(d_i,w_j)p(z_k|d_i,w_j)}$

E步骤：

$p(z_k|d_i,w_j) = \frac{p(w_j|z_k)p(z_k|d_i)}{\sum_{l=1}^K p(w_j|z_l)p(z_l|d_i)}$