无聊的递归过程

最新推荐文章于 2023-11-27 16:42:38 发布

竹影半墙

最新推荐文章于 2023-11-27 16:42:38 发布

阅读量2.9k

点赞数 2

文章标签： c语言二叉树遍历递归

本文链接：https://blog.csdn.net/misskissc/article/details/14003789

版权

碚大专栏收录该内容

410 篇文章 7 订阅

订阅专栏

编写递归函数的关键是退出递归函数的条件与递归的过程。更好诠释递归过程的是《C与指针》第7章 7.5.2节递归与迭代。

1 解递归

偶尔可能会遇到这样的题目，一个递归函数的调用叫咱求结果。假如有以下递归函数，问加入n = 5时，函数返回值为多少。

 int sum( int n)  
 {
        if(n <= 2){
              return n;
        }
        return sum(n-1) + sum(n-2);  
}

解如此的递归函数可以用笔画画，把握“C语句单步执行”和“函数调用”两规则就能够解此类递归题目。（好吧，我指的是笔试）。解此递归函数过程如下：

n = 5，n > 2，故而执行returnsum( n -1 ) + sum( n - 2)语句：

调用sum( n -1 )函数。
sum(n -1 )完毕后调用sum( n -2 )函数。
返回两个函数的和。

注：先屏蔽掉编译器的左右执行顺序，总之有一个函数先被调用，不妨假设编译器从左向右执行。不影响最后的结果。

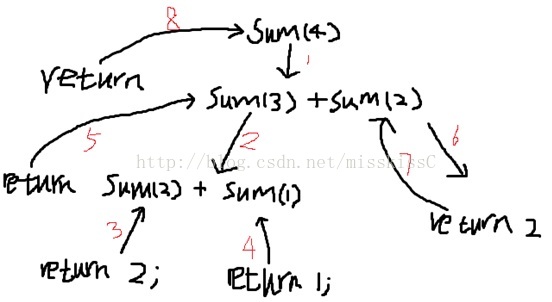
sum (n-1)的调用过程：

Figure1：sum(4)调用过程

函数调用过程跟图中序号一致，每个伴着箭头往下指的序号代表sum()函数被调用一次。得到sum(4) = 5，sum(3) = 3。

sum(3)的值也可以根据相同的过程求得，一般比较大的递归包含了较小的递归值。所以此递归解为8。

if(n <= 2){ return n; } 是递归不永久下去的关键语句，分支跳出语句。

2 递归操作过程

从递归解那里看出似乎递归先是一条道走到黑后再陆续返回去走其他的路。跟二叉树的先序遍历一个样。

在遇到递归函数时小生往往都有点搞不清楚它对对象给予了种什么操作过程。尤其是在函数中多次调用函数本身时，这种递归更让人产生扑朔迷离的感觉。因为递归函数每被调用一次后它总是要执行到递归函数的分支跳出语句后才能一层一层的返回，再执行下一条语句。这种函数对于读代码的人来说还是有那么点小可怕的。

闲着没事，分析一下快速排序递归法对序列的实际操作过程。如有序列[3，1，2，4，5，1]现用快速排序递归法将其从小到大排列，将递归语句一条条的执行一番：

分序列函数

//Part a sort to tow partion
//l is the first index of the array
//h is the max index of the array
//Retrun the l or the h
int PartSort( INT4 a[], int l, int h )
{
	if( IS_NEGATIVE(l) || IS_NEGATIVE(h) || MAX(l, h) ){
		return ;
	}
	
	INT4 temp;
	
	//Because not know the length of the a,
	//Choose the first element be the key value
	temp	= a[l];
	
	while( l < h){
		//Check elements in back
		while(h > l && a[h] >= temp){
			--h;
		}
	
		//The back element which less than the key value
		a[l]	= a[h];
	
	
		while(l < h && a[l] <= temp){
			++l;
		}
	
		a[h]	= a[l];
	}
	
	//l = h
	a[l]	= temp;

	return l;
}

递归实现

//Shell recursive
void QuickRecursive( INT4  a[],  int  l,  int  h)
{
	int m;
	if( l < h ){
		//Part array
		m	= PartSort(a, l, h);
		//Left recursive
		QuickRecursive(a, l, m - 1);
		//Right recursive
		QuickRecursive(a, m + 1, h);
	}
}

进入QuickRecursive(a, 0, 5); (1)

0< 5 调用m = PartSort(a, 0, 5);

改变的序列：

1 1 2 3 5 4

m = 3。

QuickRecursive(a,0, 2); (2)

0 < 2调用PartSort(a, 0, 2);

改变的序列：

1 1 2

m = 0;

调用QuickRecursive(a, 0, - 1); (3) 0 <-1不成立不再进入调用函数

调用QuickRecursive(a, 1, 2); (3)第3层调用排右序列

1 < 2调用PartSort(a, 1, 2);

改变的序列：

1 2

m = 1;

调用QuickRecursive(a, 1, 0); (4) 1 < 0不成立，不再进入调用函数

调用QuickRecursive(a, 2, 2); (4) 2 <2不成立，不再进入调用函数

到这里，一趟完整的递归调用完成，开始返回。一层层返回，标号为(4)的返回给标号为(3)层所调用它们的函数，标号为3的函数返回到调用它们的标号为(2)的函数。保留所有的操作排序过程。

此时函数返回到QuickRecursive(a, 0, 2); (2)

m = 3;h = 5;

开始执行下一条语句：QuickRecursive(a, 4, 5); (2)

4 < 5调用PartSort(a, 4, 5);

改变的序列：

4 5

m = 5;

函数调用QuickRecursive(a, 4, 4); (3) 4 <4不成立，不再进入调用函数

函数调用QuickRecursive(a, 5, 5); (3) 5< 5不成立，不再进入调用函数

此时，函数开始返回个上一层(2)调用他们的函数QuickRecursive(a, 4, 5);此时函数执行完毕即第(1)层的语句执行完毕返回。

此过程中得到的序列如下：

当序列较少时分析一个递归操作过程不是那么的复杂。但若序列十分的庞大，再要是需要分析出这样一个过程只怕是很难。也不必执着于递归操作过程的每一个细节，在这里我们验证了快速递归排序法操作的宏观过程：整个序列被分为两部分序列，一部分比某个数都小，另一部分比某个数都大。然后以递归所选择的递归顺序（先左序列后右序列）以相同的方划分序列，所得到的子序列仍以左子序列为先继续划分序列。直到子序列被划分为单个元素后再返回同级的右序列之上以左序列优先的顺序将同级的有序列的序列划分为单个序列。然后层层返回，再层层以左序列优先的顺序划分序列。最后得到将整个序列都划分为了单个元素的结果，即整个序列有序。好绕口，这个笔记还不如不笔记。不如一幅图来的清晰。