回溯法概述—BackTracking

1.问题的解空间

  复杂问题常常有很多的可能解，这些可能解构成了问题的解空间。解空间也就是进行穷举的搜索空间，所以，解空间中应该包括所有的可能解。确定正确的解空间很重要，如果没有确定正确的解空间就开始搜索，可能会增加很多重复解，或者根本就搜索不到正确的解。
对于任何一个问题，可能解的表示方式和它相应的解释隐含了解空间及其大小。
  例如，对于有n个物品的0/1背包问题，其可能解的表示方式可以有以下两种：
（1）可能解由一个不等长向量组成，当物品i(1≤i≤n)装入背包时，解向量中包含分量i，否则，解向量中不包含分量i，当n=3时，其解空间是：
{ ( ), (1), (2), (3), (1, 2), (1, 3), (2, 3), (1, 2, 3)}
（2）可能解由一个等长向量{x1, x2, …, xn}组成，其中xi=1(1≤i≤n)表示物品i装入背包，xi=0表示物品i没有装入背包，当n=3时，其解空间是：
{(0, 0, 0), (0, 0, 1), (0, 1, 0), (1, 0, 0), (0, 1, 1), (1, 0, 1), (1, 1, 0), (1, 1, 1) }
  为了用回溯法求解一个具有n个输入的问题，一般情况下，将其可能解表示为满足某个约束条件的 等长向量 X=(x1, x2, …, xn)，其中分量xi (1≤i≤n)的取值范围是某个有限集合Si={ai1, ai2, …, airi}，所有可能的解向量构成了问题的解空间。
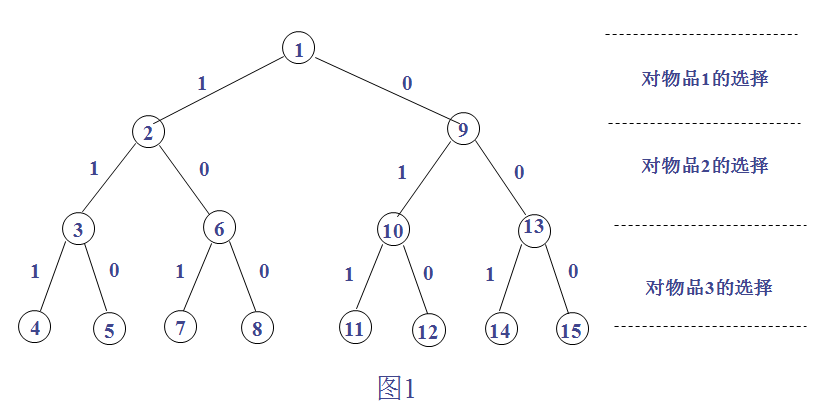
  问题的解空间一般用解空间树（Solution Space Trees,也称状态空间树）的方式组织，树的根结点位于第1层，表示搜索的初始状态，第2层的结点表示对解向量的第一个分量做出选择后到达的状态，第1层到第2层的边上标出对第一个分量选择的结果，依此类推，从树的根结点到叶子结点的路径就构成了解空间的一个可能解。
  对于n=3的0/1背包问题，其解空间树如图1所示，树中的8个叶子结点分别代表该问题的8个可能解。

  对于n=4的TSP问题，其解空间树如图2所示，树中的24个叶子结点分别代表该问题的24个可能解，例如结点5代表一个可能解，路径为1→2→3→4→1，长度为各边代价之和。