题目详情:有个长度为2n的数组{a1,a2,a3,…,an,b1,b2,b3,…,bn},希望排序后{a1,b1,a2,b2,….,an,bn},请考虑有无时间复杂度o(n),空间复杂度0(1)的解法。
问题描述
题目详情:有个长度为2n的数组{a1,a2,a3,…,an,b1,b2,b3,…,bn},希望排序后{a1,b1,a2,b2,….,an,bn},请考虑有无时间复杂度o(n),空间复杂度0(1)的解法。
题目来源:此题是2013年UC的校招笔试题,看似简单,按照题目所要排序后的字符串蛮力变化即可,但若要完美的达到题目所要求的时空复杂
度,则需要我们花费不小的精力。OK,请看下文详解,一步步优化。
解法一、蛮力变换
题目要我们怎么变换,咱们就怎么变换。此题@陈利人也分析过,在此,引用他的思路进行说明。为了便于分析,我们取n=4,那么题目要求我们把
a1,a2,a3,a4,b1,b2,b3,b4
变成
a1,b1,a2,b2,a3,b3,a4,b4
1.1、步步前移
仔细观察变换前后两个序列的特点,我们可做如下一系列操作:
确定b1的位置,即让b1跟它前面的a2,a3,a4交换: a1,b1,a2,a3,a4,b2,b3,b4
接着确定b2的位置,即让b2跟它前面的a3,a4交换: a1,b1,a2,b2,a3,a4,b3,b4
b3跟它前面的a4交换位置: a1,b1,a2,b2,a3,b3,a4,b4
b4已在最后的位置,不需要再交换。
如此,经过上述3个步骤后,得到我们最后想要的序列。但此方法的时间复杂度为O(N^2),我们得继续寻找其它方法,看看有无办法能达到题目所预期的O(N)的时间复杂度。
1.2、中间交换
当然,除了如上面所述的让b1,b2,b3,b4步步前移跟它们各自前面的元素进行交换外,我们还可以每次让序列中最中间的元素进行交换达到目的。还是用上面的例子,针对a1,a2,a3,a4,b1,b2,b3,b4
- 交换最中间的两个元素a4,b1,序列变成(待交换的元素用粗体表示):
a1,a2,a3,b1,a4,b2,b3,b4 让最中间的两对元素各自交换: a1,a2,b1,a3,b2,a4,b3,b4
交换最中间的三对元素,序列变成:a1,b1,a2,b2,a3,b3,a4,b4
同样,此法同解法1.1、步步前移一样,时间复杂度依然为O(N^2),我们得下点力气了。
解法二、完美洗牌算法
玩过扑克牌的朋友都知道,在一局完了之后洗牌,洗牌人会习惯性的把整副牌大致分为两半,两手各拿一半对着对着交叉洗牌,如下图所示
如果这副牌用a1 a2 a3 a4 b1 b2 b3 b4表示(为简化问题,假设这副牌只有8张牌),然后一分为二之后,左手上的牌可能是a1 a2 a3 a4,右手上的牌是b1 b2 b3 b4,那么在如上图那样的洗牌之后,得到的牌就可能是b1 a1 b2 a2 b3 a3 b4 a4。
技术来源于生活,2004年,microsoft的Peiyush Jain在他发表一篇名为:“A Simple In-Place Algorithm for In-Shuffle”的论文
中提出了完美洗牌算法。
这个算法解决一个什么问题呢?跟本题有什么联系呢?
完美洗牌算法解决的就是一个完美洗牌问题。什么是完美洗牌问题呢?即给定一个数组a1,a2,a3,…an,b1,b2,b3..bn,最终把它置换成b1,a1,b2,a2,…bn,an。读者可以看到,这个完美洗牌问题本质上与本题完全一致,只要在完美洗牌问题的基础上对它最后的序列swap两两相邻元素即可。
即:a1,a2,a3,…an,b1,b2,b3..bn
通过完美洗牌问题,得到:
b1,a1,b2,a2,b3,a3… bn,an
再让上面相邻的元素两两swap,即可达到本题的要求:
a1,b1,a2,b2,a3,b3….,an,bn
也就是说,如果我们能通过完美洗牌算法(时间复杂度O(N),空间复杂度O(1))解决了完美洗牌问题,也就间接解决了本题。
虽然网上已有不少文章对上篇论文或翻译或做解释说明,但对于初学者来说,理解难度实在太大,再者,若直接翻译原文,根本无法看出这个算法怎么一步步得来的,故下文将从完美洗牌算法的最基本的原型开始说起,以让读者能对此算法一目了然。
2.1、位置置换pefect_shuffle1算法
为方便讨论,我们设定数组的下标从1开始,下标范围是[1..2n]。 还是通过之前n=4的例子,来看下每个元素最终去了什么地方。
起始序列:a1 a2 a3 a4 b1 b2 b3 b4
数组下标:1 2 3 4 5 6 7 8
最终序列:b1 a1 b2 a2 b3 a3 b4 a4
从上面的例子我们能看到,前n个元素中,
第1个元素a1到了原第2个元素a2的位置,即1->2;
第2个元素a2到了原第4个元素a4的位置,即2->4;
第3个元素a3到了原第6个元素b2的位置,即3->6;
第4个元素a4到了原第8个元素b4的位置,即4->8;
那么推广到一般情况即是:前n个元素中,第i个元素去了 第(2 * i)的位置。
上面是针对前n个元素,那么针对后n个元素,可以看出:
第5个元素b1到了原第1个元素a1的位置,即5->1;
第6个元素b2到了原第3个元素a3的位置,即6->3;
第7个元素b3到了原第5个元素b1的位置,即7->5;
第8个元素b4到了原第7个元素b3的位置,即8->7;
推广到一般情况是,后n个元素,第i个元素去了第 (2 * (i - n) ) - 1 = 2 * i - (2 * n + 1) = (2 * i) % (2 * n + 1) 个位置。
再综合到任意情况,任意的第i个元素,我们最终换到了 (2 * i) % (2 * n + 1)的位置。为何呢?因为:
当0< i
// 时间O(n),空间O(n) 数组下标从1开始
void pefect_shuffle1(int *a,int n) {
int n2 = n * 2, i, b[N];
for (i = 1; i <= n2; ++i) {
b[(i * 2) % (n2 + 1)] = a[i];
}
for (i = 1; i <= n2; ++i) {
a[i] = b[i];
}
}但很明显,它的时间复杂度虽然是O(n),但其空间复杂度却是O(n),仍不符合本题所期待的时间O(n),空间O(1)。我们继续寻找更优的解法。
与此同时,我也提醒下读者,根据上面变换的节奏,我们可以看出有两个圈,
一个是1 -> 2 -> 4 -> 8 -> 7 -> 5 -> 1;
一个是3 -> 6 -> 3。
2.2、分而治之perfect_shuffle2算法
熟悉分治法的朋友,包括若看了此文的读者肯定知道,当一个问题规模比较大时,则大而化小,分而治之。对于本题,假设n是偶数,我们试着把数组从中间拆分成两半(为了方便描述,只看数组下标就够了):
- 原始数组的下标:1….2n,即(1 .. n/2, n/2+1..n)(n+1 .. n+n/2, n+n/2+1 .. 2n)
- 前半段(1 .. n/2, n/2+1..n)和后半段(n+1 .. n+n/2, n+n/2+1 .. 2n)的长度皆为n。
接下来,我们把前半段的后n/2个元素(n/2+1 .. n)和后半段的前n/2个元素(n+1..n+n/2)交换,得到 - 新的前n个元素A:(1..n/2 n+1.. n+n/2)
新的后n个元素B:(n/2+1 .. n n+n/2+1 .. 2n)
换言之,当n是偶数的时候,我们把原问题拆分成了A,B两个子问题,继而原n的求解转换成了n‘ = n/2 的求解。
可当n是奇数的时候呢?我们可以把前半段多出来的那个元素a先拿出来放到末尾,后面所有元素前移,于此,新数列的最后两个元素满足已满足要求,只需考虑前2*(n-1)个元素即可,继而转换成了n-1的问题。针对上述n分别为偶数和奇数的情况,下面举n=4和n=5两个例子来说明下。
n=4时,原始数组即为 a1 a2 a3 a4 b1 b2 b3 b4 按照之前n为偶数时的思路,把前半段的后2个元素a3 a4同后半段的前2个元素b1 b2交换,可得: a1 a2 b1 b2 a3 a4 b3 b4
因此,我们只要用pefect_shuffle1算法继续求解A(a1 a2 b1 b2)和B(a3 a4 b3 b4)两个子问题就可以了。当n=5时,原始数组则为 a1 a2 a3 a4 a5 b1 b2 b3 b4 b5
还是按照之前n为奇数时的思路,先把a5先单独拎出来放在最后,然后所有剩下的元素全部前移,变为: a1 a2 a3 a4 b1 b2 b3
b4 b5 a5 此时,最后的两个元素b5 a5已经是我们想要的结果,只要跟之前n=4的情况一样考虑即可。参考代码如下:
//时间O(nlogn) 空间O(1) 数组下标从1开始
void perfect_shuffle2(int *a,int n) {
int t,i;
if (n == 1) {
t = a[1];
a[1] = a[2];
a[2] = t;
return;
}
int n2 = n * 2, n3 = n / 2;
if (n % 2 == 1) { //奇数的处理
t = a[n];
for (i = n + 1; i <= n2; ++i) {
a[i - 1] = a[i];
}
a[n2] = t;
--n;
}
//到此n是偶数
for (i = n3 + 1; i <= n; ++i) {
t = a[i];
a[i] = a[i + n3];
a[i + n3] = t;
}
// [1.. n /2]
perfect_shuffle2(a, n3);
perfect_shuffle2(a + n, n3);
} 分析下此算法的复杂度: 每次,我们交换中间的n个元素,需要O(n)的时间,n是奇数的话,我们还需要O(n)的时间先把后两个元素调整好,但这不
影响总体时间复杂度。
《算法导论》中文第二版44页的主定理,可最终解得T(n) = O(nlogn)。至于空间,此算法在数组内部折腾的,
所以是O(1)(在不考虑递归的栈的空间的前提下)。
2.3、完美洗牌算法perfect_shuffle3
2.3.1、走圈算法cycle_leader
因为之前无论是perfect_shuffle1,还是perfect_shuffle2,这两个算法的均未达到时间复杂度O(N)并且空间复杂度O(1)的要求,所以我们必须得再找一种新的方法,以期能完美的解决本节开头提出的完美洗牌问题。
让我们先来回顾一下2.1节位置置换perfect_shuffle1算法,还记得我之前提醒读者的关于当n=4时,通过位置置换让每一个元素到了最后的位置时,所形成的两个圈么?我引用下2.1节的相关内容:
当n=4的情况:
起始序列:a1 a2 a3 a4 b1 b2 b3 b4
数组下标:1 2 3 4 5 6 7 8
最终序列:b1 a1 b2 a2 b3 a3 b4 a4
即通过置换,我们得到如下结论:
“于此同时,我也提醒下读者,根据上面变换的节奏,我们可以看出有两个圈,
一个是1 -> 2 -> 4 -> 8 -> 7 -> 5 -> 1;
一个是3 -> 6 -> 3。”
这两个圈可以表示为(1,2,4,8,7,5)和(3,6),且perfect_shuffle1算法也已经告诉了我们,不管你n是奇数还是偶数,每个位置的元素都将变为第
(2*i) % (2n+1)个元素:
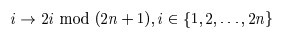
因此我们只要知道圈里最小位置编号的元素即圈的头部,顺着圈走一遍就可以达到目的,且因为圈与圈是不想交的,所以这样下来,我们刚好走了O(N)步。
还是举n=4的例子,且假定我们已经知道第一个圈和第二个圈的前提下,要让1 2 3 4 5 6 7 8变换成5 1 2 7 3 8 4:
第一个圈:1 -> 2 -> 4 -> 8 -> 7 -> 5 -> 1
第二个圈:3 -> 6 -> 3:
原始数组:1 2 3 4 5 6 7 8
数组小标:1 2 3 4 5 6 7 8
走第一圈:5 1 3 2 7 6 8 4
走第二圈:5 1 6 2 7 3 8 4
上面沿着圈走的算法我们给它取名为cycle_leader,这部分代码如下:
//数组下标从1开始,from是圈的头部,mod是要取模的数 mod 应该为 2 * n + 1,时间复杂度O(圈长)
void cycle_leader(int *a,int from, int mod) {
int last = a[from],t,i;
for (i = from * 2 % mod;i != from; i = i * 2 % mod) {
t = a[i];
a[i] = last;
last = t;
}
a[from] = last;
} 2.3.2、神级结论:若2*n=(3^k - 1),则可确定圈的个数及各自头部的起始位置
下面我要引用此论文“A Simple In-Place Algorithm for In-Shuffle”的一个结论了,
即,对于2*n = (3^k-1)这种长度的数组,恰好只有k个圈,且每个圈头部的起始位置分别是1,3,9,...3^(k-1)。
论文原文部分为:
也就是说,利用上述这个结论,我们可以解决这种特殊长度2*n = (3^k-1)的数组问题,那么若给定的长度n是任意的咋办呢?此时,我们可以借鉴2.2节、分而治之算法的思想,把整个数组一分为二,即拆分成两个部分:
让一部分的长度满足神级结论:若2*m = (3^k-1),则恰好k个圈,且每个圈头部的起始位置分别是1,3,9,…3^(k-1)。其中m小于n,m往神级结论所需的值上套;剩下的n-m部分单独计算;
当把n分解成m和n-m两部分后,原始数组对应的下标如下(为了方便描述,我们依然只需要看数组下标就够了):
原始数组下标:1..m m+1.. n, n+1 .. n+m, n+m+1,..2*n
参照之前2.2节、分而治之算法的思路,且更为了能让前部分的序列满足神级结论2*m = (3^k-1),我们可以把中间那两段长度为n-m和m的段交换位置,即相当于把m+1..n,n+1..n+m的段循环右移m次(为什么要这么做?因为如此操作后,数组的前部分的长度为2m,而根据神级结论:当2m=3^k-1时,可知这长度2m的部分恰好有k个圈)。而如果读者看过本系列第一章、左旋转字符串的话,就应该意识到循环位移是有O(N)的算法的,其思想即是把前n-m个元素(m+1.. n)和后m个元素(n+1 .. n+m)先各自翻转一下,再将整个段(m+1.. n, n+1 .. n+m)翻转下。
这个翻转的代码如下:
//翻转字符串时间复杂度O(to - from)
void reverse(int *a,int from,int to) {
int t;
for (; from < to; ++from, --to) {
t = a[from];
a[from] = a[to];
a[to] = t;
}
}
//循环右移num位 时间复杂度O(n)
void right_rotate(int *a,int num,int n) {
reverse(a, 1, n - num);
reverse(a, n - num + 1,n);
reverse(a, 1, n);
} 翻转后,得到的目标数组的下标为:
目标数组下标:1..m n+1..n+m m+1 .. n n+m+1,..2*n
当给定n=7时,若要满足神级结论2*n=3^k-1,k只能取2,继而推得n‘=m=4。
原始数组:a1 a2 a3 a4 (a5 a6 a7) ( b1 b2 b3 b4 ) b5 b6 b7
既然m=4,即让上述数组中有括号的两个部分交换,得到:
目标数组:a1 a2 a3 a4 b1 b2 b3 b4 a5 a6 a7 b5 b6 b7
继而目标数组中的前半部分a1 a2 a3 a4 b1 b2 b3 b4部分可以用2.3.1、走圈算法cycle_leader搞定,
于此我们最终求解的n长度变成了n’=3,即n的长度减小了4,单独再解决后半部分a5 a6 a7 b5 b6 b7即可。
2.3.3、完美洗牌算法perfect_shuffle3
从上文的分析过程中也就得出了我们的完美洗牌算法,其算法流程为:
输入数组 A[1..2 * n]
找到 2 * m = 3^k - 1 使得 3^k <= 2 * n < 3^(k +1)
把a[m + 1..n + m]那部分循环移m位
对每个i = 0,1,2..k - 1,3^i是个圈的头部,做cycle_leader算法,数组长度为m,所以对2 * m + 1取模。
对数组的后面部分A[2 * m + 1.. 2 * n]继续使用本算法, 这相当于n减小了m。
上述算法流程对应的论文原文为:
以上各个步骤对应的时间复杂度分析如下:
因为循环不断乘3的,所以时间复杂度O(logn)
循环移位O(n)
- 每个圈,每个元素只走了一次,一共2*m个元素,所以复杂度omega(m), 而m < n,所以 也在O(n)内。
T(n - m)
因此总的时间复杂度为 T(n) = T(n - m) + O(n) ,m = omega(n) ,解得:T(n) = O(n)。
此完美洗牌算法实现的参考代码如下:
//时间O(n),空间O(1)
void perfect_shuffle3(int *a,int n) {
int n2, m, i, k,t;
for (;n > 1;) {
// step 1
n2 = n * 2;
for (k = 0, m = 1; n2 / m >= 3; ++k, m *= 3)
;
m /= 2;
// 2m = 3^k - 1 , 3^k <= 2n < 3^(k + 1)
// step 2
right_rotate(a + m, m, n);
// step 3
for (i = 0, t = 1; i < k; ++i, t *= 3) {
cycle_leader(a , t, m * 2 + 1);
}
//step 4
a += m * 2;
n -= m;
}
// n = 1
t = a[1];
a[1] = a[2];
a[2] = t;
} 2.3.4、perfect_shuffle3算法解决其变形问题
以上代码即解决了完美洗牌问题,那么针对本章要解决的其变形问题呢?是的,如本章开头所说,
在完美洗牌问题的基础上对它最后的序列swap两两相邻元素即可,代码如下:
//时间复杂度O(n),空间复杂度O(1),数组下标从1开始,调用perfect_shuffle3
void shuffle(int *a,int n) {
int i,t,n2 = n * 2;
perfect_shuffle3(a,n);
for (i = 2; i <= n2; i += 2) {
t = a[i - 1];
a[i - 1] = a[i];
a[i] = t;
}
} 上述的这个“在完美洗牌问题的基础上对它最后的序列swap两两相邻元素”的操作
(当然,你也可以让原数组第一个和最后一个不变,中间的2 * (n - 1)项用原始的标准完美洗牌算法做),
只是在完美洗牌问题时间复杂度O(N)空间复杂度O(1)的基础上再增加O(N)的时间复杂度,
故总的时间复杂度O(N)不变,且理所当然的保持了空间复杂度O(1)。至此,咱们的问题得到了圆满解决!
参考网址
【1】程序员编程艺术第三十四~三十五章:格子取数问题,完美洗牌算法 - 结构之法 算法之道 - 博客频道 - CSDN.NET
http://blog.csdn.net/v_july_v/article/details/10212493#t8
【2】面试算法:格子取数问题,完美洗牌算法-面试题-about云开发 http://www.aboutyun.com/thread-9995-1-1.html
【3】完美洗牌算法 - 推酷
http://www.tuicool.com/articles/rUju2m



























 547
547

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








