第三十四~三十五章:格子取数,完美洗牌算法
时间:二零一三年八月二十三日。
题记
再过一个半月,即到2013年10月11日,便是本博客开通3周年之际,巧的是,那天刚好也是我的25岁生日。写博近3年,访问量趋近500万,无法确切知道帮助了多少人影响了多少人,但有些文章和一些系列是我比较喜欢的,如这三篇:从B树、B+树、B*树谈到R 树;教你如何迅速秒杀掉:99%的海量数据处理面试题;支持向量机通俗导论(理解SVM的三层境界)。
- 第三十四章:格子取数问题;
- 第三十五章:完美洗牌算法的变形
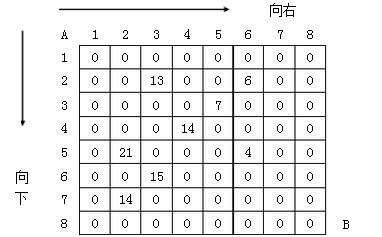
第三十四章、格子取数问题
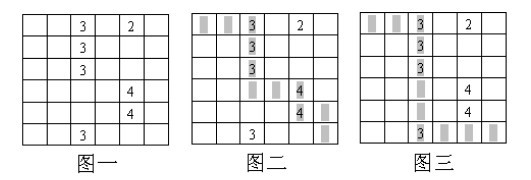
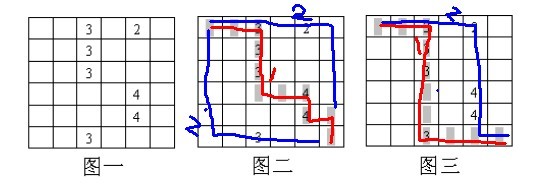
- 如果按照上面的局部贪优走法,那么第一次势必会如图二那样走,导致的结果是第二次要么取到2,要么取到3,
- 但若不按照上面的局部贪优走法,那么第一次可以如图三那样走,从而第二次走的时候能取到2 4 4,很显然,这种走法求得的最终SUM值更大;
解法一、直接搜索
//copyright@西芹_new 2013
#include "stdafx.h"
#include <iostream>
using namespace std;
#define N 5
int map[5][5]={
{2,0,8,0,2},
{0,0,0,0,0},
{0,3,2,0,0},
{0,0,0,0,0},
{2,0,8,0,2}};
int sumMax=0;
int p1x=0;
int p1y=0;
int p2x=0;
int p2y=0;
int curMax=0;
void dfs( int index){
if( index == 2*N-2){
if( curMax>sumMax)
sumMax = curMax;
return;
}
if( !(p1x==0 && p1y==0) && !(p2x==N-1 && p2y==N-1))
{
if( p1x>= p2x && p1y >= p2y )
return;
}
//right right
if( p1x+1<N && p2x+1<N ){
p1x++;p2x++;
int sum = map[p1x][p1y]+map[p2x][p2y];
curMax += sum;
dfs(index+1);
curMax -= sum;
p1x--;p2x--;
}
//down down
if( p1y+1<N && p2y+1<N ){
p1y++;p2y++;
int sum = map[p1x][p1y]+map[p2x][p2y];
curMax += sum;
dfs(index+1);
curMax -= sum;
p1y--;p2y--;
}
//rd
if( p1x+1<N && p2y+1<N ) {
p1x++;p2y++;
int sum = map[p1x][p1y]+map[p2x][p2y];
curMax += sum;
dfs(index+1);
curMax -= sum;
p1x--;p2y--;
}
//dr
if( p1y+1<N && p2x+1<N ) {
p1y++;p2x++;
int sum = map[p1x][p1y]+map[p2x][p2y];
curMax += sum;
dfs(index+1);
curMax -= sum;
p1y--;p2x--;
}
}
int _tmain(int argc, _TCHAR* argv[])
{
curMax = map[0][0];
dfs(0);
cout <<sumMax-map[N-1][N-1]<<endl;
return 0;
} 解法二、动态规划
上述解法一的搜索解法是的时间复杂度是指数型的,如果是只走一次的话,是经典的dp。
2.1、DP思路详解
故正如@绿色夹克衫所说:此题也可以用动态规划求解,主要思路就是同时DP 2次所走的状态。
1、先来分析一下这个问题,为了方便讨论,先对矩阵做一个编号,且以5*5的矩阵为例(给这个矩阵起个名字叫M1):
M1
0 1 2 3 4
1 2 3 4 5
2 3 4 5 6
3 4 5 6 7
4 5 6 7 8
从左上(0)走到右下(8)共需要走8步(2*5-2)。我们设所走的步数为s。因为限定了只能向右和向下走,因此无论如何走,经过8步后(s = 8)都将走到右下。而DP的状态也是依据所走的步数来记录的。
再来分析一下经过其他s步后所处的位置,根据上面的讨论,可以知道:
- 经过8步后,一定处于右下角(8);
- 那么经过5步后(s = 5),肯定会处于编号为5的位置;
- 3步后肯定处于编号为3的位置;
- s = 4的时候,处于编号为4的位置,此时对于方格中,共有5(相当于n)个不同的位置,也是所有编号中最多的。
故推广来说,对于n*n的方格,总共需要走2n - 2步,且当s = n - 1时,编号为n个,也是编号数最多的。
如果用DP[s,i,j]来记录2次所走的状态获得的最大值,其中s表示走s步,i和j分别表示在s步后第1趟走的位置和第2趟走的位置。
2、为了方便描述,再对矩阵做一个编号(给这个矩阵起个名字叫M2):
M2
0 0 0 0 0
1 1 1 1 1
2 2 2 2 2
3 3 3 3 3
4 4 4 4 4
把之前定的M1矩阵也再贴下:
M1
0 1 2 3 4
1 2 3 4 5
2 3 4 5 6
3 4 5 6 7
4 5 6 7 8
我们先看M1,在经过6步后,肯定处于M1中编号为6的位置。而M1中共有3个编号为6的,它们分别对应M2中的2 3 4。故对于M2来说,假设第1次经过6步走到了M2中的2,第2次经过6步走到了M2中的4,DP[s,i,j] 则对应 DP[6,2,4]。由于s = 2n - 2,0 <= i<= <= j <= n,所以这个DP共有O(n^3)个状态。
M1
0 1 2 3 4
1 2 3 4 5
2 3 4 5 6
3 4 5 6 7
4 5 6 7 8
再来分析一下状态转移,以DP[6,2,3]为例(就是上面M1中加粗的部分),可以到达DP[6,2,3]的状态包括DP[5,1,2],DP[5,1,3],DP[5,2,2],DP[5,2,3]。
3、下面,我们就来看看这几个状态:DP[5,1,2],DP[5,1,3],DP[5,2,2],DP[5,2,3],用加粗表示位置DP[5,1,2] DP[5,1,3] DP[5,2,2] DP[5,2,3] (加红表示要达到的状态DP[6,2,3])
0 1 2 3 4 0 1 2 3 4 0 1 2 3 4 0 1 2 3 4
1 2 3 4 5 1 2 3 4 5 1 2 3 4 5 1 2 3 4 5
2 3 4 5 6 2 3 4 5 6 2 3 4 5 6 2 3 4 5 6
3 4 5 6 7 3 4 5 6 7 3 4 5 6 7 3 4 5 6 7
4 5 6 7 8 4 5 6 7 8 4 5 6 7 8 4 5 6 7 8
因此:
DP[6,2,3] = Max(DP[5,1,2] ,DP[5,1,3],DP[5,2,2],DP[5,2,3]) + 6,2和6,3格子中对应的数值 (式一)
上面(式一)所示的这个递推看起来没有涉及:“如果两次经过同一个格子,那么该数只加一次的这个条件”,讨论这个条件需要换一个例子,以DP[6,2,2]为例:DP[6,2,2]可以由DP[5,1,1],DP[5,1,2],DP[5,2,2]到达,但由于i = j,也就是2次走到同一个格子,那么数值只能加1次。
所以当i = j时,
DP[6,2,2] = Max(DP[5,1,1],DP[5,1,2],DP[5,2,2]) + 6,2格子中对应的数值 (式二)
4、故,综合上述的(式一),(式二)最后的递推式就是
if(i != j)
DP[s, i ,j] = Max(DP[s - 1, i - 1, j - 1], DP[s - 1, i - 1, j], DP[s - 1, i, j - 1], DP[s - 1, i, j]) + W[s,i] + W[s,j]
else
DP[s, i ,j] = Max(DP[s - 1, i - 1, j - 1], DP[s - 1, i - 1, j], DP[s - 1, i, j]) + W[s,i]
2.2、DP方法实现
//copyright@caopengcs 2013
const int N = 202;
const int inf = 1000000000; //无穷大
int dp[N * 2][N][N];
bool isValid(int step,int x1,int x2,int n) { //判断状态是否合法
int y1 = step - x1, y2 = step - x2;
return ((x1 >= 0) && (x1 < n) && (x2 >= 0) && (x2 < n) && (y1 >= 0) && (y1 < n) && (y2 >= 0) && (y2 < n));
}
int getValue(int step, int x1,int x2,int n) { //处理越界 不存在的位置 给负无穷的值
return isValid(step, x1, x2, n)?dp[step][x1][x2]:(-inf);
}
//状态表示dp[step][i][j] 并且i <= j, 第step步 两个人分别在第i行和第j行的最大得分 时间复杂度O(n^3) 空间复杂度O(n^3)
int getAnswer(int a[N][N],int n) {
int P = n * 2 - 2; //最终的步数
int i,j,step;
//不能到达的位置 设置为负无穷大
for (i = 0; i < n; ++i) {
for (j = i; j < n; ++j) {
dp[0][i][j] = -inf;
}
}
dp[0][0][0] = a[0][0];
for (step = 1; step <= P; ++step) {
for (i = 0; i < n; ++i) {
for (j = i; j < n; ++j) {
dp[step][i][j] = -inf;
if (!isValid(step, i, j, n)) { //非法位置
continue;
}
//对于合法的位置进行dp
if (i != j) {
dp[step][i][j] = max(dp[step][i][j], getValue(step - 1, i - 1, j - 1, n));
dp[step][i][j] = max(dp[step][i][j], getValue(step - 1, i - 1, j, n));
dp[step][i][j] = max(dp[step][i][j], getValue(step - 1, i, j - 1, n));
dp[step][i][j] = max(dp[step][i][j], getValue(step - 1, i, j,n));
dp[step][i][j] += a[i][step - i] + a[j][step - j]; //不在同一个格子,加两个数
}
else {
dp[step][i][j] = max(dp[step][i][j], getValue(step - 1, i - 1, j - 1, n));
dp[step][i][j] = max(dp[step][i][j], getValue(step - 1, i - 1, j, n));
dp[step][i][j] = max(dp[step][i][j], getValue(step - 1, i, j, n));
dp[step][i][j] += a[i][step - i]; // 在同一个格子里,只能加一次
}
}
}
}
return dp[P][n - 1][n- 1];
}复杂度分析:状态转移最多需要统计4个变量的情况,看做是O(1)的,共有O(n^3)个状态,所以总的时间复杂度是O(n^3)的,且dp数组开了N^3大小,故其空间复杂度亦为O(n^3)。
2.3、DP实现优化版
即我们在推算dp[step]的时候,只依靠它上一次的状态dp[step - 1],所以dp数组的第一维,我们只开到2就可以了。即step为奇数时,我们用dp[1][i][j]表示状态,step为偶数我们用dp[0][i][j]表示状态,这样我们只需要O(n^2)的空间,这就是滚动数组的方法。滚动数组写起来并不复杂,只需要对上面的代码稍作修改即可,优化后的代码如下:
//copyright@caopengcs 8/24/2013
int dp[2][N][N];
bool isValid(int step,int x1,int x2,int n) { //判断状态是否合法
int y1 = step - x1, y2 = step - x2;
return ((x1 >= 0) && (x1 < n) && (x2 >= 0) && (x2 < n) && (y1 >= 0) && (y1 < n) && (y2 >= 0) && (y2 < n));
}
int getValue(int step, int x1,int x2,int n) { //处理越界 不存在的位置 给负无穷的值
return isValid(step, x1, x2, n)?dp[step % 2][x1][x2]:(-inf);
}
//状态表示dp[step][i][j] 并且i <= j, 第step步 两个人分别在第i行和第j行的最大得分 时间复杂度O(n^3) 使用滚动数组 空间复杂度O(n^2)
int getAnswer(int a[N][N],int n) {
int P = n * 2 - 2; //最终的步数
int i,j,step,s;
//不能到达的位置 设置为负无穷大
for (i = 0; i < n; ++i) {
for (j = i; j < n; ++j) {
dp[0][i][j] = -inf;
}
}
dp[0][0][0] = a[0][0];
for (step = 1; step <= P; ++step) {
for (i = 0; i < n; ++i) {
for (j = i; j < n; ++j) {
dp[step][i][j] = -inf;
if (!isValid(step, i, j, n)) { //非法位置
continue;
}
s = step % 2; //状态下表标
//对于合法的位置进行dp
if (i != j) {
dp[s][i][j] = max(dp[s][i][j], getValue(step - 1, i - 1, j - 1, n));
dp[s][i][j] = max(dp[s][i][j], getValue(step - 1, i - 1, j, n));
dp[s][i][j] = max(dp[s][i][j], getValue(step - 1, i, j - 1, n));
dp[s][i][j] = max(dp[s][i][j], getValue(step - 1, i, j,n));
dp[s][i][j] += a[i][step - i] + a[j][step - j]; //不在同一个格子,加两个数
}
else {
dp[s][i][j] = max(dp[s][i][j], getValue(step - 1, i - 1, j - 1, n));
dp[s][i][j] = max(dp[s][i][j], getValue(step - 1, i - 1, j, n));
dp[s][i][j] = max(dp[s][i][j], getValue(step - 1, i, j, n));
dp[s][i][j] += a[i][step - i]; // 在同一个格子里,只能加一次
}
}
}
}
return dp[P % 2][n - 1][n- 1];
}第三十五章、完美洗牌算法
解法一、蛮力变换
a1,a2,a3,a4, b1,b2,b3,b4
a1, b1,a2,b2, a3,b3, a4, b4
1.1、步步前移
a1, b1,a2,a3,a4, b2,b3,b4
a1, b1,a2, b2,a3,a4, b3,b4
a1, b1,a2, b2,a3, b3,a4, b4
1.2、中间交换
a1,a2,a3,b1, a4,b2,b3,b4
a1,a2, b1,a3, b2,a4, b3,b4
a1, b1,a2, b2,a3, b3,a4, b4
同样,此法同解法1.1、步步前移一样,时间复杂度依然为O(N^2),我们得下点力气了。
解法二、完美洗牌算法
a1,a2,a3,...an, b1,b2,b3..bn
b1,a1, b2,a2, b3,a3... bn,an
a1, b1,a2, b2,a3, b3....,an, bn
2.1、位置置换pefect_shuffle1算法
数组下标:1 2 3 4 5 6 7 8
最终序列:b1 a1 b2 a2 b3 a3 b4 a4
从上面的例子我们能看到,前n个元素中,
- 第1个元素a1到了原第2个元素a2的位置,即1->2;
- 第2个元素a2到了原第4个元素a4的位置,即2->4;
- 第3个元素a3到了原第6个元素b2的位置,即3->6;
- 第4个元素a4到了原第8个元素b4的位置,即4->8;
- 第5个元素b1到了原第1个元素a1的位置,即5->1;
- 第6个元素b2到了原第3个元素a3的位置,即6->3;
- 第7个元素b3到了原第5个元素b1的位置,即7->5;
- 第8个元素b4到了原第7个元素b3的位置,即8->7;
- 当0< i <n时, 原式= (2i) % (2 * n + 1) = 2i;
- 当i>n时,原式(2 * i) % (2 * n + 1)保持不变。
// 时间O(n),空间O(n) 数组下标从1开始
void pefect_shuffle1(int *a,int n) {
int n2 = n * 2, i, b[N];
for (i = 1; i <= n2; ++i) {
b[(i * 2) % (n2 + 1)] = a[i];
}
for (i = 1; i <= n2; ++i) {
a[i] = b[i];
}
}- 一个是1 -> 2 -> 4 -> 8 -> 7 -> 5 -> 1;
- 一个是3 -> 6 -> 3。
2.2、分而治之perfect_shuffle2算法
原始数组的下标:1....2n,即(1 .. n/2, n/2+1..n)( n+1 .. n+n/2, n+n/2+1 .. 2n)
前半段(1 .. n/2, n/2+1..n)和后半段(n+1 .. n+n/2, n+n/2+1 .. 2n)的长度皆为n。
新的前n个元素A:(1..n/2 n+1.. n+n/2)
新的后n个元素B:( n/2+1 .. n n+n/2+1 .. 2n)
a1 a2 a3 a4 b1 b2 b3 b4
a1 a2 b1 b2 a3 a4 b3 b4
a1 a2 a3 a4 a5 b1 b2 b3 b4 b5
a1 a2 a3 a4 b1 b2 b3 b4 b5 a5
//copyright@caopengcs 8/23/2013
//时间O(nlogn) 空间O(1) 数组下标从1开始
void perfect_shuffle2(int *a,int n) {
int t,i;
if (n == 1) {
t = a[1];
a[1] = a[2];
a[2] = t;
return;
}
int n2 = n * 2, n3 = n / 2;
if (n % 2 == 1) { //奇数的处理
t = a[n];
for (i = n + 1; i <= n2; ++i) {
a[i - 1] = a[i];
}
a[n2] = t;
--n;
}
//到此n是偶数
for (i = n3 + 1; i <= n; ++i) {
t = a[i];
a[i] = a[i + n3];
a[i + n3] = t;
}
// [1.. n /2]
perfect_shuffle2(a, n3);
perfect_shuffle2(a + n, n3);
} 2.3、完美洗牌算法perfect_shuffle3
2.3.1、走圈算法cycle_leader
数组下标:1 2 3 4 5 6 7 8
最终序列:b1 a1 b2 a2 b3 a3 b4 a4
“ 于此同时,我也提醒下读者,根据上面变换的节奏,我们可以看出有两个圈,
- 一个是1 -> 2 -> 4 -> 8 -> 7 -> 5 -> 1;
- 一个是3 -> 6 -> 3。”
第一个圈:1 -> 2 -> 4 -> 8 -> 7 -> 5 -> 1
第二个圈:3 -> 6 -> 3:
原始数组: 1 2 3 4 5 6 7 8
数组小标:1 2 3 4 5 6 7 8
走第一圈: 5 1 3 2 7 6 8 4
走第二圈:5 1 6 2 7 3 8 4
//数组下标从1开始,from是圈的头部,mod是要取模的数 mod 应该为 2 * n + 1,时间复杂度O(圈长)
void cycle_leader(int *a,int from, int mod) {
int last = a[from],t,i;
for (i = from * 2 % mod;i != from; i = i * 2 % mod) {
t = a[i];
a[i] = last;
last = t;
}
a[from] = last;
}2.3.2、神级结论:若2*n=(3^k - 1),则可确定圈的个数及各自头部的起始位置
- 对于2*n = (3^k-1)这种长度的数组,恰好只有k个圈,且每个圈头部的起始位置分别是1,3,9,...3^(k-1)。
也就是说,利用上述这个结论,我们可以解决这种特殊长度2*n = (3^k-1)的数组问题,那么若给定的长度n是任意的咋办呢?此时,我们可以借鉴2.2节、分而治之算法的思想,把整个数组一分为二,即拆分成两个部分:
- 让一部分的长度满足神级结论:若2*m = (3^k-1),则恰好k个圈,且每个圈头部的起始位置分别是1,3,9,...3^(k-1)。其中m<n,m往神级结论所需的值上套;
- 剩下的n-m部分单独计算;
当把n分解成m和n-m两部分后,原始数组对应的下标如下(为了方便描述,我们依然只需要看数组下标就够了):
原始数组下标:1..m m+1.. n, n+1 .. n+m, n+m+1,..2*n
参照之前2.2节、分而治之算法的思路,且更为了能让前部分的序列满足神级结论2*m = (3^k-1),我们可以把中间那两段长度为n-m和m的段交换位置,即相当于把m+1..n,n+1..n+m的段循环右移m次(为什么要这么做?因为如此操作后,数组的前部分的长度为2m,而根据神级结论:当2m=3^k-1时,可知这长度2m的部分恰好有k个圈)。
而如果读者看过本系列第一章、左旋转字符串的话,就应该意识到循环位移是有O(N)的算法的,其思想即是把前n-m个元素(m+1.. n)和后m个元素(n+1 .. n+m)先各自翻转一下,再将整个段(m+1.. n, n+1 .. n+m)翻转下。
这个翻转的代码如下:
//翻转字符串时间复杂度O(to - from)
void reverse(int *a,int from,int to) {
int t;
for (; from < to; ++from, --to) {
t = a[from];
a[from] = a[to];
a[to] = t;
}
}
//循环右移num位 时间复杂度O(n)
void right_rotate(int *a,int num,int n) {
reverse(a, 1, n - num);
reverse(a, n - num + 1,n);
reverse(a, 1, n);
}翻转后,得到的目标数组的下标为:
目标数组下标:1..m n+1..n+m m+1 .. n n+m+1,..2*n
OK,理论讲清楚了,再举个例子便会更加一目了然。当给定n=7时,若要满足神级结论2*n=3^k-1,k只能取2,继而推得n‘=m=4。
原始数组:a1 a2 a3 a4 a5 a6 a7 b1 b2 b3 b4 b5 b6 b7
既然m=4,即让上述数组中有下划线的两个部分交换,得到:
目标数组:a1 a2 a3 a4 b1 b2 b3 b4 a5 a6 a7 b5 b6 b7
继而目标数组中的前半部分a1 a2 a3 a4 b1 b2 b3 b4部分可以用2.3.1、走圈算法cycle_leader搞定,于此我们最终求解的n长度变成了n’=3,即n的长度减小了4,单独再解决后半部分a5 a6 a7 b5 b6 b7即可。
2.3.3、完美洗牌算法perfect_shuffle3
从上文的分析过程中也就得出了我们的完美洗牌算法,其算法流程为:
- 输入数组 A[1..2 * n]
- step 1 找到 2 * m = 3^k - 1 使得 3^k <= 2 * n < 3^(k +1)
- step 2 把a[m + 1..n + m]那部分循环移m位
- step 3 对每个i = 0,1,2..k - 1,3^i是个圈的头部,做cycle_leader算法,数组长度为m,所以对2 * m + 1取模。
- step 4 对数组的后面部分A[2 * m + 1.. 2 * n]继续使用本算法, 这相当于n减小了m。
以上各个步骤对应的时间复杂度分析如下:
- 因为循环不断乘3的,所以时间复杂度O(logn)
- 循环移位O(n)
- 每个圈,每个元素只走了一次,一共2*m个元素,所以复杂度omega(m), 而m < n,所以 也在O(n)内。
- T(n - m)
此完美洗牌算法实现的参考代码如下:
//copyright@caopengcs 8/24/2013
//时间O(n),空间O(1)
void perfect_shuffle3(int *a,int n) {
int n2, m, i, k,t;
for (;n > 1;) {
// step 1
n2 = n * 2;
for (k = 0, m = 1; n2 / m >= 3; ++k, m *= 3)
;
m /= 2;
// 2m = 3^k - 1 , 3^k <= 2n < 3^(k + 1)
// step 2
right_rotate(a + m, m, n);
// step 3
for (i = 0, t = 1; i < k; ++i, t *= 3) {
cycle_leader(a , t, m * 2 + 1);
}
//step 4
a += m * 2;
n -= m;
}
// n = 1
t = a[1];
a[1] = a[2];
a[2] = t;
}2.3.4、perfect_shuffle3算法解决其变形问题
啊哈!以上代码即解决了完美洗牌问题,那么针对本章要解决的其变形问题呢?是的,如本章开头所说,在完美洗牌问题的基础上对它最后的序列swap两两相邻元素即可,代码如下:
//copyright@caopengcs 8/24/2013
//时间复杂度O(n),空间复杂度O(1),数组下标从1开始,调用perfect_shuffle3
void shuffle(int *a,int n) {
int i,t,n2 = n * 2;
perfect_shuffle3(a,n);
for (i = 2; i <= n2; i += 2) {
t = a[i - 1];
a[i - 1] = a[i];
a[i] = t;
}
}上述的这个“在完美洗牌问题的基础上对它最后的序列swap两两相邻元素”的操作(当然,你也可以让原数组第一个和最后一个不变,中间的2 * (n - 1)项用原始的标准完美洗牌算法做),只是在完美洗牌问题时间复杂度O(N)空间复杂度O(1)的基础上再增加O(N)的时间复杂度,故总的时间复杂度O(N)不变,且理所当然的保持了空间复杂度O(1)。至此,咱们的问题得到了圆满解决!
2.3.5、神级结论是如何来的?
我们的问题得到了解决,但本章尚未完,即决定完美洗牌算法的神级结论:若2*n=(3^k - 1),则恰好只有k个圈,且每个圈头部的起始位置分别是1,3,9,...3^(k-1),是如何来的呢?
要证明这个结论的关键就是:这所有的圈合并起来必须包含从1到M之间的所有证书,一个都不能少。这个证明有点麻烦,因为证明过程中会涉及到群论等数论知识,但再远的路一步步走也能到达。
首先,让咱们明确以下相关的概念,定理,及定义(搞清楚了这些东西,咱们便证明了一大半):
- 概念1 mod表示对一个数取余数,比如3 mod 5 =3,5 mod 3 =2;
- 定义1 欧拉函数ϕ(m) 表示为不超过m(即小于等于m)的数中,与m互素的正整数个数
- 定义2 若ϕ(m)=Ordm(a) 则称a为m的原根,其中Ordm(a)定义为:a ^d ( mod m),其中d=0,1,2,3…,但取让等式成立的最小的那个d。
结合上述定义1、定义2可知,2是3的原根,因为2^0 mod 3 = 1, 2^1 mod 3 = 2, 2^2 mod 3 = 1, 2^3 mod 3 = 2,{a^0 mod m,a^1 mod m,a^2}得到集合S={1,2},包含了所有和3互质的数,也即d=ϕ(3)=2,满足原根定义。
而2不是7的原根,这是因为2^0 mod 7 = 1, 2^1 mod 7 = 2, 2^2 mod 7 = 4, 2^3 mod 7 = 1,2^4 mod 7 = 2,2^5 mod 7 = 4,2^6 mod 7 = 1,从而集合S={1,2,4}中始终只有1、2、4三种结果,而没包含全部与7互质的数(3、6、5便不包括),,即d=3,但ϕ(7)=6,从而d != ϕ(7),不满足原根定义。
再者,如果说一个数a,是另外一个数m的原根,代表集合S = {a^0 mod m, a^1 mod m, a^2 mod m…… },得到的集合包含了所有小于m并且与m互质的数,否则a便不是m的原根。而且集合S = {a^0 mod m, a^1 mod m, a^2 mod m…… }中可能会存在重复的余数,但当a与m互质的时候,得到的{a^0 mod m, a^1 mod m, a^2 mod m}集合中,保证了第一个数是a^0 mod m,故第一次发现重复的数时,这个重复的数一定是1,也就是说,出现余数循环一定是从开头开始循环的。
- 定义3 对模指数,a对模m的原根定义为
,st:
中最小的正整数d
再比如,2是9的原根,因为,为了让
除以9的余数恒等于1,可知最小的正整数d=6,而ϕ(m)=6,满足原根的定义。
- 定理1 同余定理:两个整数
a,b
,若它们除以正整数m
所得的余数相等,则称a
,b
对于模
m同余,记作
,读做a与b关于模m同余。
- 定理2 当p为奇素数且a是
的原根时⇒ a也是
的原根
- 定理3 费马小定理:如果a和m互质,那么a^ϕ(m) mod m = 1
- 定理4 若(a,m)=1 且a为m的原根,那么a是(Z/mZ)*的生成元。
我们知道2是3的原根,2是9的原根,我们定义S(k)表示上述的集合S,并且取x = 3^k(x表示为集合S中的数)。
所以:
S(1) = {1, 2}
S(2) = {1, 2, 4, 8, 7, 5}
也就是说S(k - t)里每个数x* 3^t形成的新集合包含了所有与3^k的最大公约数为3^t的数,它也是一个圈,原先圈的头部是1,这个圈的头部是3^t。
于是,对所有的小于 3^k的数,根据它和3^k的最大公约数,我们都把它分配到了一个圈里去了,且k个圈包含了所有的小于3^k的数。
下面,举个例子,如caopengcs所说,当我们取“a = 2, m = 3时,
所以S(1) = {1, 2}
S(2) = {1, 2, 4, 8, 7, 5}
- S(3) = {1, 2 ,4 , 8, 16, 5, 10, 20, 13, 26, 25, 23, 19, 11, 22, 17, 7, 14} 包含了小于27且与27互质的所有数,圈的首部为1,这是原根定义决定的。
- 那么与27最大公约数为3的数,我们用S(2)中的数乘以3得到。 S(2) * 3 = {3, 6, 12, 24, 21, 15}, 圈中元素的顺序没变化,圈的首部是3。
- 与27最大公约数为9的数,我们用S(1)中的数乘以9得到。 S(1) * 9 = {9, 18}, 圈中得元素的顺序没变化,圈的首部是9。
换言之,若定义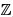
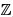
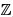
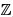 /N ={0,1,2,3,.....,26},
(
/N ={0,1,2,3,.....,26},
(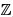 /N)*
相当于就是{0,1,2,3,.....,26}中全部与27互素的数的集合;
/N)*
相当于就是{0,1,2,3,.....,26}中全部与27互素的数的集合;
而2^k(mod 27)可以把(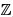
- 取头为1,(
/27)*={1,2,4,8,16,5,10,20,13,26,25,23,19,11,22,17,7,14},也就是说,与27互素且小于27的正整数集合为{1,2,4,8,16,5,10,20,13,26,25,23,19,11,22,17,7,14},因此ϕ(m) = ϕ(27)=18, 从而满足
的最小d = 18,故得出2为27的原根;
- 取头为3,就可以得到{3,6,12,24,21,15},这就是以3为头的环,这个圈的特点是所有的数都是3的倍数,且都不是9的倍数。为什么呢?因为2^k和27互素。
具体点则是:如果3×2^k除27的余数能够被9整除,则有一个n使得3*2^k=9n(mod 27),即3*2^k-9n能够被27整除,从而3*2^k-9n=27m,其中n,m为整数,这样一来,式子约掉一个3,我们便能得到2^k=9m+3n,也就是说,2^k是3的倍数,这与2^k与27互素是矛盾的,所以,3×2^k除27的余数不可能被9整除。
此外,2^k除以27的余数可以是3的倍数以外的所有数,所以,2^k除以27的余数可以为1,2,4,5,7,8,当余数为1时,即存在一个k使得2^k-1=27m,m为整数。
式子两边同时乘以3得到:3*2^k-3=81m是27的倍数,从而3*2^k除以27的余数为3;
同理,当余数为2时,2^k - 2 = 27m,=> 3*2^k- 6 =81m,从而3*2^k除以27的余数为6;
当余数为4时,2^k - 4 = 37m,=> 3*2^k - 12 =81m,从而3*2^k除以27的余数为12;
同理,可以取到15,21,24。从而也就印证了上面的结论:取头为3,就可以得到{3,6,12,24,21,15}。
- 取9为头,这就很简单了,这个圈就是{9,18}
因为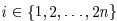
i = 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27
由于n=13,2n+1 = 27,据此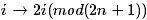
i = 2 4 6 8 10 12 14 16 18 20 22 24 26 1 3 5 7 9 11 13 15 17 19 21 23 25 0
根据i 和 i‘ 前后位置的变动,我们将得到3个圈:
- 1
2
 4
4 8
8 16
16 5
5 10
10 20
20 13
13 26
26 25
25 23
23 19
19 11
11 22
22 17
17 7
7 14
14 1;
1; - 3
6
12
24
21
15
3
- 9
18
9
2.3.6、完美洗牌问题的几个扩展
至此,本章开头提出的问题解决了,完美洗牌算法的证明也证完了,是否可以止步了呢?OH,NO!读者有无思考过下述问题:
- 既然完美洗牌问题是给定输入:a1,a2,a3,……aN,b1,b2,b3,……bN,要求输出:b1,a1,b2,a2,……bN,aN;那么有无考虑过它的逆问题:即给定b1,a1,b2,a2,……bN,aN,,要求输出a1,a2,a3,……aN,b1,b2,b3,……bN ?
- 完美洗牌问题是两手洗牌,假设有三只手同时洗牌呢?那么问题将变成:输入是a1,a2,……aN, b1,b2,……bN, c1,c2,……cN,要求输出是c1,b1,a1,c2,b2,a2,……cN,bN,aN,这个时候,怎么处理?
本第35章完。
参考链接
- huangxy10,http://blog.csdn.net/huangxy10/article/details/8071242;
- @绿色夹克衫,http://www.51nod.com/answer/index.html#!answerId=598;
- 格子取数的蛮力穷举法:http://wenku.baidu.com/view/681c853b580216fc700afd9a.html;
- @陈立人,http://mp.weixin.qq.com/mp/appmsg/show?__biz=MjM5ODIzNDQ3Mw==&appmsgid=10000141&itemidx=1&sign=4f1aa1a2269a1fac88be49c8cba21042;
- caopengcs,http://blog.csdn.net/caopengcs/article/details/10196035;
- 完美洗牌算法的原始论文“A Simple In-Place Algorithm for In-Shuffle”,http://att.newsmth.net/att.php?p.1032.47005.1743.pdf;
- 原始根模:http://en.wikipedia.org/wiki/Primitive_root_modulo_n;
- 洗牌的学问:http://www.thecodeway.com/blog/?p=680;
- 关于完美洗牌算法:http://cs.stackexchange.com/questions/332/in-place-algorithm-for-interleaving-an-array/400#400;
- 关于完美洗牌算法中圈的说明:http://www.emis.de/journals/DMTCS/pdfpapers/dm050111.pdf;
- 关于神级结论的讨论:http://math.stackexchange.com/questions/477125/how-to-prove-algebraic-structure-of-the-perfect-shuffle(左边链接中的讨论中有错误,以在本文2.3.5节进行了相关修正);
- caopengcs关于神级结论的证明:http://blog.csdn.net/caopengcs/article/details/10429013;
- 同余的概念:http://zh.wikipedia.org/wiki/%E5%90%8C%E9%A4%98;
- 神奇的费马小定理:http://www.xieguofang.cn/Maths/Number_Theory/Fermat's_Little_Theorem_1.htm;
- 完美洗牌问题的几个扩展:http://blog.csdn.net/caopengcs/article/details/10521603;
- 原根与指数的介绍:http://wenku.baidu.com/view/bbb88ffc910ef12d2af9e738;
- 《数论概论》Joseph H. Silverman著,推荐理由:因写上文中的完美洗牌算法遇到了一堆数论定理受了刺激,故推荐此书;
 格子取数与完美洗牌算法
格子取数与完美洗牌算法






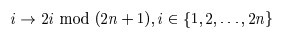




















 1076
1076

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










