【计算几何各种知识点总结】[不定期补充]

计算几何模板总结 ：

http://blog.csdn.net/qq_33184171/article/details/51124611

精度控制

尽量不要用除法，三角函数，强制类型转换（尤其是double转int）等操作，否则精度损失比较大 。
const double PI = acos(-1.0);
const double EPS = 1e-8;
对小数点后1位 取整 的方法为 ±1 （+1位进位 -1为退位）
eg：8(double)=7.9999999999….;
8(int)=8;
int(8(double))=7; !!!!!!
这样精度损失就大了~~~~

杂点

精度问题

1.在用1e-n判断相等的时候不是n越大越好 要选择合适的 ，一般为6/8/9/10
2.判断两条线段距离大小关系的时候有平方倍进行比较。
3.未完待续。。。

点与其他图形的位置关系

点与直线的位置关系

首先明确点与直线的位置关系只有两种：
1.点在直线上

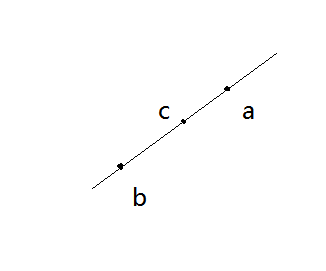
2.点不在直线上

在这里只要用叉积判断就可以了
以上图为例只需满足向量$a\cdot b \times a\cdot c=0$即可
如果叉积等于0 则说明两向量共线 所以点在直线上
如果叉积不为0 则说明点不在直线上

点与线段的关系

知道了如何判断点与直线的位置关系在来判断点与线段的位置关系就容易多了
跟直线类似点与线段也只有两种位置关系：
1.点在线段上
2.点不在线段上

如果点在线段上则需满足以下两种情况：
1.点在线段所在的直线上。
2.点在以线段为对角线的矩形内。
前者很好理解，而后者则确保点不在线段的两端延长线上。
所以除了判断叉积还要判断坐标关系
以下图为例

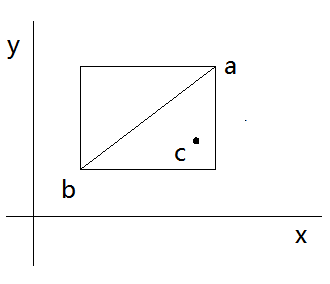
很容易得出
应满足以下结论

c.x> min(a.x,b.x);
c.x< max(a.x,b.x);
c.y> min(a.y,b.y);
c.y< max(a.y,b.y);
这样就满足了点在矩形内
当然不能忘记用叉积判断；；；

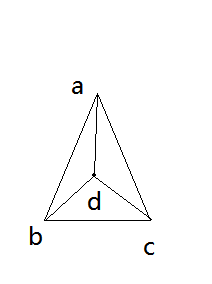
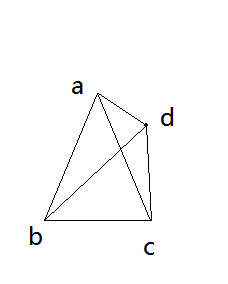
点与三角形的内外

先要说明，当点在三角形边上的时候视为点在三角形的内部
在这里我们运用面积关系来判断点在三角形的内外

观察S△dab+S△dbc+S△dac与S△abc的大小关系
观察上两图不难发现当点在三角形内是S△dab+S△dbc+S△dac是相等于S△abc的
而点在三角线外的时候
S△dab+S△dbc+S△dac是大于S△abc的

所以只要计算出两式的大小关系即可
Ps：这里求面积运用的为叉乘,$\overrightarrow{ab} \times\overrightarrow{ac}$就是 延伸出去的平行四边形的面积
$S△_{abc}=\dfrac{\overrightarrow{ab} \times\overrightarrow{ac}}{2}$；

判断大小关系的时候不用除以2 直接判断即可 且更加精确

线段相交

判断两线段是否相交

判断两个线段是否相交，要先想一下两条线段之间都有什么样的位置关系。
1.相离

2.相交