一.定义
•从某顶点出发,沿图的边到达另一顶点所经过的路径中,各边上权值之和最小的一条路径——最短路径。
•最短路径一共有四种算法来实现,今天在这里我先介绍下其中的三种方法,Floyd算法,Dijkstra算法,Bellman-Ford算法。其中Floyd算法可以求解任意两点间的最短路径的长度,它的时间复杂度是O(n³)
• 而Dijkstra算法 Bellman-Ford算法是以某一点为起点来求解其到某一点的最短路径的长度。
二.Floyd算法
1.基本思想:
从任意节点A到任意节点B的最短路径不外乎2种可能,1是直接从A到B,2是从A经过若干个节点到B。所以,我们假设dis(AB)为节点A到节点B的最短路径的距离,对于每一个节点K,我们检查dis(AK)
+ dis(KB) < dis(AB)是否成立,如果成立,证明从A到K再到B的路径比A直接到B的路径短,我们便设置 dis(AB) = dis(AK) +
dis(KB),这样一来,当我们遍历完所有节点K,dis(AB)中记录的便是A到B的最短路径的距离。这道题就运用到了dp的思想。
或许有些人听了上面的话后会这样写代码
for (int i=1; i<=n;i++)
{
for(int j=1;j<=n;j++)
{
for (int k=1; k<=n;k++)
{
dis[i][j]=min(dis[i][j],dis[i][k]+dis[k][j]);
}
}
}但是这里我们要注意循环的嵌套顺序,如果把检查所有节点K放在最内层,那么结果将是不正确的,为什么呢?因为这样便过早的把i到j的最短路径确定下来了,而当后面存在更短的路径时,已经不再会更新了。
就像下面出现的情况一样
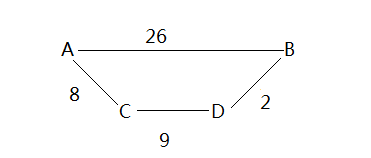
按照上面你的代码从A到B只能找到一条路径 那就是AB 权值为26 但显然这是不对的 对于AC-CD-DB这条路而已 加起来权值也仅仅只有19 权值小于直接A到B 造成错误的原因就是我们把检查所有节点K放在最内层,造成过早的把A到B的最短路径确定下来了,当确定A->B的最短路径时dis(AC)尚未被计算。所以,我们需要改写循环顺序,如下:
for(int k=1;k<=n;k++)//中间点
{
for(int i=1;i<=n;i++)//起始点
{
for(int j=1;j<=n;j++)//终点
{
if(i!=j&&j!=k)
{
dis[i][j]=min(dis[i][j],dis[i][k]+dis[k][j]);
}
}
}
}2.Floyd算法模板
#include <iostream>
#include <cstdio>
#include <cstring>
#include <cstdlib>
#include <algorithm>
#include <map>
#include <cmath>
#include <queue>
#include <string>
#include <vector>
#include <set>
using namespace std;
#define ll long long
#define sc(x) scanf("%d",&x)
#define dsc(x,y) scanf("%d%d",&x,&y)
#define sssc(x) scanf("%s",s)
#define sdsc(x,y) scanf("%s %s",x,y)
#define ssc(x,y,z) scanf("%d%d%d",&x,&y,&z)
#define pr(x) printf("%d\n",x)
#define FOR(i,n,o) for(int i=o;i<=n;i++)
#define lcr(a,b) memset(a,b,sizeof(a))
#define Inf 1<<29
int n,m;
int mp[100][100];
int main()
{
while(~dsc(n,m))//n个点 m条路
{
FOR(i,n,1)
{
FOR(j,n,1)
{
if(i!=j)
{
mp[i][j]=Inf;//初始化为极大值
}
else
{
mp[i][j]=0;//自己和自己的距离为0
}
}
}
FOR(i,m,1)
{
int a,b,c;
sc(a);
sc(b);
sc(c);
mp[a][b]=c;
//mp[b][a]=c; 无向图
}
FOR(k,n,1)//中间点
{
FOR(i,n,1)//起始点
{
FOR(j,n,1)//终点
{
if(i!=j&&j!=k)
{
mp[i][j]=min(mp[i][j],mp[i][k]+mp[k][j]);//dp的思想
}
}
}
}
FOR(i,n,1)
{
FOR(j,n,1)
{
printf("dis %d %d =%d\n",i,j,mp[i][j]);//打印当前某两个点的最短路径
}
}
}
return 0;
}三.Dijkstra算法
1.基本思想:
Dijkstra算法是以一个点为起点开始查询到其他点的最短路径的,其时间复杂度为O(n²),如果查询所有的点的话和Floyd算法的时间复杂度就变成一样的了,同样是O(n³),和不久前所学的最小生成树的普利姆算法有异曲同工之妙,运用的贪心的思想,利用局面最小解来解决这类问题。
Dijkstra算法按路径长度,递增次序产生最短路径。利用双重for循环去查找dis[i] 1到i的最短路径 找到后再两for循环之间添加一个更新for循环更新dis[i]的值
2.Dijkstra算法模板
#include <iostream>
#include <cstdio>
#include <cstring>
#include <cstdlib>
#include <algorithm>
#include <map>
#include <cmath>
#include <queue>
#include <string>
#include <vector>
#include <set>
using namespace std;
#define ll long long
#define sc(x) scanf("%d",&x)
#define dsc(x,y) scanf("%d%d",&x,&y)
#define sssc(x) scanf("%s",s)
#define sdsc(x,y) scanf("%s %s",x,y)
#define ssc(x,y,z) scanf("%d%d%d",&x,&y,&z)
#define pr(x) printf("%d\n",x)
#define FOR(i,n,o) for(int i=o;i<=n;i++)
#define lcr(a,b) memset(a,b,sizeof(a))
#define Inf 1<<29
int mp[100][100];
int dis[100];
int vis[100];
int n,m;
void dij(int s)
{
FOR(i,n,1)
{
vis[i]=0;//初始化全部未使用
dis[i]=mp[s][i];//dis数组记录1到i的最短路径
}
vis[s]=1;//标记s使用过
dis[s]=0;//标记s到自己的路径为0
FOR(i,n,1)
{
int to=-1;
int d=Inf;
FOR(j,n,1)
{
if(!vis[j]&&d>dis[j])
{
d=dis[j];
to=j;
}
}
vis[to]=1;
FOR(j,n,1)
{
if(!vis[j]&&dis[j]>dis[to]+mp[to][j])
dis[j]=dis[to]+mp[to][j];
}
}
return ;
}
int main()
{
while(~dsc(n,m))//n个点 m条路
{
FOR(i,n,1)
{
FOR(j,n,1)
{
if(i!=j)
mp[i][j]=Inf;//初始化极大值
else
mp[i][j]=0;//自己和自己距离为0
}
}
FOR(i,m,1)
{
int a,b,c;
ssc(a,b,c);
mp[a][b]=c;//无向图
mp[b][a]=c;
}
dij(1);//以第一个点开始
FOR(i,n,2)//打印点1到其他点的最短路径
{
printf("%d %d\n",i,dis[i]);
}
}
return 0;
}注意:上面这种方法是无法处理负权值边的,下面我要讲的算法则可以处理负权值边的,因为它加入了一种新的判断。
四.Bellman-Ford(贝尔曼)算法
1.基本思想
Dijkstra算法无法判断含负权边的图的最短路。如果遇到负权,在没有负权回路存在时(负权回路的含义是,回路的权值和为负。)即便有负权的边,也可以采用Bellman-Ford算法正确求出最短路径,。
Bellman-Ford算法能在更普遍的情况下(存在负权边)解决单源点最短路径问题。对于给定的带权(有向或无向)图
G=(V,E),其源点为s,加权函数 w是 边集 E
的映射。对图G运行Bellman-Ford算法的结果是一个布尔值,表明图中是否存在着一个从源点s可达的负权回路。若不存在这样的回路,算法将给出从源点s到
图G的任意顶点v的最短路径d[v]。
另外贝尔曼算法的时间复杂度为O(n*m) n个点m条边
2.Bellman-Ford(贝尔曼)算法模板
#include <iostream>
#include <cstdio>
#include <cstring>
#include <cstdlib>
#include <algorithm>
#include <map>
#include <cmath>
#include <queue>
#include <string>
#include <vector>
#include <set>
using namespace std;
#define ll long long
#define sc(x) scanf("%d",&x)
#define dsc(x,y) scanf("%d%d",&x,&y)
#define sssc(x) scanf("%s",s)
#define sdsc(x,y) scanf("%s %s",x,y)
#define ssc(x,y,z) scanf("%d%d%d",&x,&y,&z)
#define pr(x) printf("%d\n",x)
#define FOR(i,n,o) for(int i=o;i<=n;i++)
#define lcr(a,b) memset(a,b,sizeof(a))
#define Inf 1<<29
int mp[100][100];
int dis[100];
int vis[100];
struct node
{
int u;
int v;
int w;
}q[105];
int n,m;
int bellman_floyd(int s)
{
FOR(i,n,1)
{
dis[i]=Inf;//初始化为极大值
}
dis[s]=0;
FOR(i,n-1,1)
{
for(int j=1;j<=2*m;j++)
{
if(dis[q[j].u]+q[j].w<dis[q[j].v])
dis[q[j].v]=dis[q[j].u]+q[j].w;
}
}
for(int i=1;i<=2*m;i++)
{
if(dis[q[i].u]+q[i].w<dis[q[i].v])
return -1;//浮旋回路
}
return 1;
}
int main()
{
while(~dsc(n,m))//n个点 m条路
{
int cnt=0;
for(int i=1;i<=2*m;i+=2)//因为是无向图 所有要这样输入 边界也是2*m
{
ssc(q[i].u,q[i].v,q[i].w);
q[i+1].v=q[i].u;
q[i+1].u=q[i].v;
q[i+1].w=q[i].w;
}
int x=bellman_floyd(1);//以1为起点查找和其他点的最短路径
if(x==-1)
printf("no\n");
else
{
FOR(i,n,1)
{
printf("dis %d %d\n",i,dis[i]);
}
}
}
return 0;
}
END!!!!!!!!!!!!!!!!!!!!!























 2093
2093











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








