首先为了防止混淆,我这里用了自已定义的一些变量
i 在样本中遍历,样本数量为m
j 在特征中遍历,特征数量为n
k 在分类中遍历,分类数量为c
In these notes, we describe the Softmax regression model. This model generalizes logistic regression to classification problems where the class label y can take on more than two possible values. This will be useful for such problems as MNIST digit classification, where the goal is to distinguish between 10 different numerical digits. Softmax regression is a supervised learning algorithm, but we will later be using it in conjuction with our deep learning/unsupervised feature learning methods.
Recall that in logistic regression, we had a training set
{(x(1),y(1)),…,(x(m),y(m))}
of m labeled examples, where the input features are
x(i)∈Rn+1
. (In this set of notes, we will use the notational convention of letting the feature vectors x be n + 1 dimensional, with
x0=1
corresponding to the intercept term.) With logistic regression, we were in the binary classification setting, so the labels were
y(i)∈{0,1}
. Our hypothesis took the form:
and the model parameters θ were trained to minimize the cost function
In the softmax regression setting, we are interested in multi-class classification (as opposed to only binary classification), and so the label y can take on
c
different values, rather than only two. Thus, in our training set
Given a test input x, we want our hypothesis to estimate the probability that
p(y=k|x)
for each value of
k=1,…,c
. I.e., we want to estimate the probability of the class label taking on each of the
c
different possible values. Thus, our hypothesis will output a k dimensional vector (whose elements sum to 1) giving us our
Here θ1,θ2,…,θc∈Rn+1 are the parameters of our model. Notice that the term 1∑ck=1eθTkx(i) normalizes the distribution, so that it sums to one.
For convenience, we will also write θ to denote all the parameters of our model. When you implement softmax regression, it is usually convenient to represent
Cost Function
We now describe the cost function that we’ll use for softmax regression. In the equation below, 1{⋅} is the indicator function, so that 1{a true statement} = 1, and 1{a false statement} = 0. For example, 1{2 + 2 = 4} evaluates to 1; whereas 1{1 + 1 = 5} evaluates to 0. Our cost function will be:
Notice that this generalizes the logistic regression cost function, which could also have been written:
The softmax cost function is similar, except that we now sum over the k different possible values of the class label. Note also that in softmax regression, we have that
p(y(i)=k|x(i);θ)=eθTkx(i)∑cl=1eθTlx(i)
.
There is no known closed-form way to solve for the minimum of J(θ), and thus as usual we’ll resort to an iterative optimization algorithm such as gradient descent or L-BFGS. Taking derivatives, one can show that the gradient is:
Recall the meaning of the “
∇θj
” notation. In particular,
∇θkJ(θ)
is itself a vector, so that its j-th element is
∂J(θ)∂θkj
the partial derivative of J(θ) with respect to the j-th element of
θk
.
Armed with this formula for the derivative, one can then plug it into an algorithm such as gradient descent, and have it minimize J(θ). For example, with the standard implementation of gradient descent, on each iteration we would perform the update
θk:=θk−α∇θkJ(θ)
(for each
k=1,…,c
).
When implementing softmax regression, we will typically use a modified version of the cost function described above; specifically, one that incorporates weight decay. We describe the motivation and details below.
Properties of softmax regression parameterization
Softmax regression has an unusual property that it has a “redundant” set of parameters. To explain what this means, suppose we take each of our parameter vectors
θk
, and subtract some fixed vector
ψ
from it, so that every
In other words, subtracting ψ from every
Further, if the cost function J(θ) is minimized by some setting of the parameters (θ1,θ2,…,θc) , then it is also minimized by (θ1−ψ,θ2−ψ,…,θc−ψ) for any value of ψ . Thus, the minimizer of
Notice also that by setting ψ=θ1 , one can always replace θ1 with θ1−ψ=0⃗ (the vector of all 0’s), without affecting the hypothesis. Thus, one could “eliminate” the vector of parameters θ1 (or any other θk , for any single value of k ), without harming the representational power of our hypothesis. Indeed, rather than optimizing over the
In practice, however, it is often cleaner and simpler to implement the version which keeps all the parameters (θ1,θ2,…,θc) , without arbitrarily setting one of them to zero. But we will make one change to the cost function: Adding weight decay. This will take care of the numerical problems associated with softmax regression’s overparameterized representation.
但是这里我们除了Weight Decay外,还是减去最大值,原因如下
However, when the products θTkx(i) are large, the exponential function eθTkx(i) will become very very large and possibly overflow. To prevent overflow, we can simply subtract some large constant value from each of the θTkx(i) terms before computing the exponential. In practice, for each example, you can use the maximum of the θTkx(i) terms as the constant.
这里的a为行向量,其中每列的元素为矩阵 θTx 对应列 θTx(i) 中的最大的元素
注意这里
θ
为
c∗n
的矩阵,
x
为
Weight Decay
We will modify the cost function by adding a weight decay term λ2∑ck=1∑nj=0θ2kj which penalizes large values of the parameters. Our cost function is now
With this weight decay term (for any λ>0 ), the cost function J(θ) is now strictly convex, and is guaranteed to have a unique solution. The Hessian is now invertible, and because J(θ) is convex, algorithms such as gradient descent, L-BFGS, etc. are guaranteed to converge to the global minimum.
To apply an optimization algorithm, we also need the derivative of this new definition of J(θ) . One can show that the derivative is:
这里对 J(θ) 求导得到的结果,推导如下:
注意这里用到了公式:
∂xTa∂x=∂aTx∂x=a
(引用于matrix cookbook 2.4.1)

note: In particular,
∇θkJ(θ)
is itself a vector, so that its j-th element is
∂J(θ)∂θkj
the partial derivative of J(θ) with respect to the j-th element of
θk
.
By minimizing J(θ) with respect to θ <script type="math/tex" id="MathJax-Element-87">θ</script>, we will have a working implementation of softmax regression.
下面提供源码
// Softmax regression
#include <iostream>
#include <armadillo>
#include <math.h>
using namespace arma;
using namespace std;
#define elif else if
#define MAX_ITER 1000000
double cost = 0.0;
mat grad;
double lrate = 0.1;
double lambda = 0.0;
int nclasses = 2;
colvec vec2colvec(vector<double>& vec) {
int length = vec.size();
colvec A(length);
for (int i = 0; i<length; i++) {
A(i) = vec[i];
}
return A;
}
rowvec vec2rowvec(vector<double>& vec) {
colvec A = vec2colvec(vec);
return A.t();
}
mat vec2mat(vector<vector<double> >&vec) {
int cols = vec.size();
int rows = vec[0].size();
mat A(rows, cols);
for (int i = 0; i<rows; i++) {
for (int j = 0; j<cols; j++) {
A(i, j) = vec[j][i];
}
}
return A;
}
void update_CostFunction_and_Gradient(mat x, rowvec y, mat weightsMatrix, double lambda) {
int nsamples = x.n_cols;
int nfeatures = x.n_rows;
//calculate cost function
mat theta(weightsMatrix);
mat M = theta * x;
mat temp = repmat(max(M, 0), nclasses, 1);
M = M - temp;
M = arma::exp(M);
temp = repmat(sum(M, 0), nclasses, 1);
M = M / temp;
mat groundTruth = zeros<mat>(nclasses, nsamples);
for (int i = 0; i<y.size(); i++) {
groundTruth(y(i), i) = 1;//对y的数据进行归类
}
temp = groundTruth % (arma::log(M));
cost = -accu(temp) / nsamples;
cost += accu(arma::pow(theta, 2)) * lambda / 2;
//calculate gradient
temp = groundTruth - M;
temp = temp * x.t();
grad = -temp / nsamples;
grad += lambda * theta;
}
rowvec calculateY(mat x, mat weightsMatrix) {
mat theta(weightsMatrix);
mat M = theta * x;
mat temp = repmat(max(M, 0), nclasses, 1);
M = M - temp;
M = arma::exp(M);
temp = repmat(sum(M, 0), nclasses, 1);
M = M / temp;
M = arma::log(M);
rowvec result = zeros<rowvec>(M.n_cols);
for (int i = 0; i<M.n_cols; i++) {
int maxele = INT_MIN;
int which = 0;
for (int j = 0; j<M.n_rows; j++) {
if (M(j, i) > maxele) {
maxele = M(j, i);
which = j;
}
}
result(i) = which;
}
return result;
}
void softmax(vector<vector<double> >&vecX, vector<double> &vecY, vector<vector<double> >& testX, vector<double>& testY) {
int nsamples = vecX.size();
int nfeatures = vecX[0].size();
//change vecX and vecY into matrix or vector.
rowvec y = vec2rowvec(vecY);
mat x = vec2mat(vecX);
double init_epsilon = 0.12;
mat weightsMatrix = randu<mat>(nclasses, nfeatures);
weightsMatrix = weightsMatrix * (2 * init_epsilon) - init_epsilon;
grad = zeros<mat>(nclasses, nfeatures);
/*
//Gradient Checking (remember to disable this part after you're sure the
//cost function and dJ function are correct)
update_CostFunction_and_Gradient(x, y, weightsMatrix, lambda);
mat dJ(grad);
cout<<"test!!!!"<<endl;
double epsilon = 1e-4;
for(int i=0; i<weightsMatrix.n_rows; i++){
for(int j=0; j<weightsMatrix.n_cols; j++){
double memo = weightsMatrix(i, j);
weightsMatrix(i, j) = memo + epsilon;
update_CostFunction_and_Gradient(x, y, weightsMatrix, lambda);
double value1 = cost;
weightsMatrix(i, j) = memo - epsilon;
update_CostFunction_and_Gradient(x, y, weightsMatrix, lambda);
double value2 = cost;
double tp = (value1 - value2) / (2 * epsilon);
cout<<i<<", "<<j<<", "<<tp<<", "<<dJ(i, j)<<endl;
weightsMatrix(i, j) = memo;
}
}
*/
int converge = 0;
double lastcost = 0.0;
while (converge < MAX_ITER) {
update_CostFunction_and_Gradient(x, y, weightsMatrix, lambda);
weightsMatrix -= lrate * grad;
cout << "learning step: " << converge << ", Cost function value = " << cost << endl;
if (fabs((cost - lastcost)) <= 5e-6 && converge > 0) break;
lastcost = cost;
++converge;
}
cout << "############result#############" << endl;
rowvec yT = vec2rowvec(testY);
mat xT = vec2mat(testX);
rowvec result = calculateY(xT, weightsMatrix);
rowvec error = yT - result;
int correct = error.size();
for (int i = 0; i<error.size(); i++) {
if (error(i) != 0) --correct;
}
cout << "correct: " << correct << ", total: " << error.size() << ", accuracy: " << double(correct) / (double)(error.size()) << endl;
}
int main(int argc, char** argv)
{
long start, end;
//read training X from .txt file
FILE *streamX, *streamY;
streamX = fopen("trainX.txt", "r");
int numofX = 30;
vector<vector<double> > vecX;
double tpdouble;
int counter = 0;
while (1) {
if (fscanf(streamX, "%lf", &tpdouble) == EOF) break;
if (counter / numofX >= vecX.size()) {
vector<double> tpvec;
vecX.push_back(tpvec);
}
vecX[counter / numofX].push_back(tpdouble);
++counter;
}
fclose(streamX);
cout << vecX.size() << ", " << vecX[0].size() << endl;
//read training Y from .txt file
streamY = fopen("trainY.txt", "r");
vector<double> vecY;
while (1) {
if (fscanf(streamY, "%lf", &tpdouble) == EOF) break;
vecY.push_back(tpdouble);
}
fclose(streamY);
for (int i = 1; i<vecX.size(); i++) {
if (vecX[i].size() != vecX[i - 1].size()) return 0;
}
if (vecX.size() != vecY.size()) return 0;
streamX = fopen("testX.txt", "r");
vector<vector<double> > vecTX;
counter = 0;
while (1) {
if (fscanf(streamX, "%lf", &tpdouble) == EOF) break;
if (counter / numofX >= vecTX.size()) {
vector<double> tpvec;
vecTX.push_back(tpvec);
}
vecTX[counter / numofX].push_back(tpdouble);
++counter;
}
fclose(streamX);
streamY = fopen("testY.txt", "r");
vector<double> vecTY;
while (1) {
if (fscanf(streamY, "%lf", &tpdouble) == EOF) break;
vecTY.push_back(tpdouble);
}
fclose(streamY);
start = clock();
softmax(vecX, vecY, vecTX, vecTY);
end = clock();
cout << "Training used time: " << ((double)(end - start)) / CLOCKS_PER_SEC << " second" << endl;
return 0;
}然后,对照源码我们看下该算法是如何实现的
FILE *streamX, *streamY;
streamX = fopen("trainX.txt", "r");
int numofX = 30;
vector<vector<double> > vecX;
double tpdouble;
int counter = 0;
while (1) {
if (fscanf(streamX, "%lf", &tpdouble) == EOF) break;
if (counter / numofX >= vecX.size()) {
vector<double> tpvec;
vecX.push_back(tpvec);
}
vecX[counter / numofX].push_back(tpdouble);
++counter;
}
fclose(streamX);这部分将trainX.txt的数据读入vecX中,
trainX.txt每行有30个数据,一共有284行
所以vecX外层大小为284, 内层大小为30
表示成矩阵 284 * 30
同理,我们来看TrainY.txt的数据
//read training Y from .txt file
streamY = fopen("trainY.txt", "r");
vector<double> vecY;
while (1) {
if (fscanf(streamY, "%lf", &tpdouble) == EOF) break;
vecY.push_back(tpdouble);
}
fclose(streamY);trainY.txt每行有1个数据,一共有284行
表示成矩阵 284 * 1
同理, testX 和 textY 分别跟 trainX 和 trainY一样大小
然后我们看softmax函数
int nsamples = vecX.size();//284
int nfeatures = vecX[0].size();//30
//change vecX and vecY into matrix or vector.
rowvec y = vec2rowvec(vecY);
mat x = vec2mat(vecX);// x 30 * 284
double init_epsilon = 0.12;
mat weightsMatrix = randu<mat>(nclasses, nfeatures);//weightsMatrix 2 * 30 这个矩阵就是需要求的θ系数.对于每种分类,对应一个不同的θ向量,该向量有n个分量
weightsMatrix = weightsMatrix * (2 * init_epsilon) - init_epsilon;//给需要求的θ一个初值
grad = zeros<mat>(nclasses, nfeatures); //grad 2 * 30 int converge = 0;
double lastcost = 0.0;
while (converge < MAX_ITER) {
update_CostFunction_and_Gradient(x, y, weightsMatrix, lambda);
weightsMatrix -= lrate * grad;
cout << "learning step: " << converge << ", Cost function value = " << cost << endl;
if (fabs((cost - lastcost)) <= 5e-6 && converge > 0) break;
lastcost = cost;
++converge;接着我们看下update_CostFunction_and_Gradient
void update_CostFunction_and_Gradient(mat x, rowvec y, mat weightsMatrix, double lambda) {
int nsamples = x.n_cols;//284
int nfeatures = x.n_rows;//30
//calculate cost function
mat theta(weightsMatrix);
mat M = theta * x; // theta:2*30 x:30*284 M:2*284
mat temp = repmat(max(M, 0), nclasses, 1); // temp:2*284 每列中元素相同,为M对应列中的最大的元素
M = M - temp;//相当于上面描述中减去a
M = arma::exp(M);//分子
temp = repmat(sum(M, 0), nclasses, 1);//分母
M = M / temp;
mat groundTruth = zeros<mat>(nclasses, nsamples);//groundTruth: 2*284
for (int i = 0; i<y.size(); i++) { // y:284*1
groundTruth(y(i), i) = 1;//对y的数据进行归类
}
temp = groundTruth % (arma::log(M));//grounTruth相当1{y(i)=k}
cost = -accu(temp) / nsamples;
cost += accu(arma::pow(theta, 2)) * lambda / 2;
//calculate gradient
temp = groundTruth - M;
temp = temp * x.t();
grad = -temp / nsamples;
grad += lambda * theta;
}然后后面就是用梯度下降法进行迭代,代码我就不多解释了








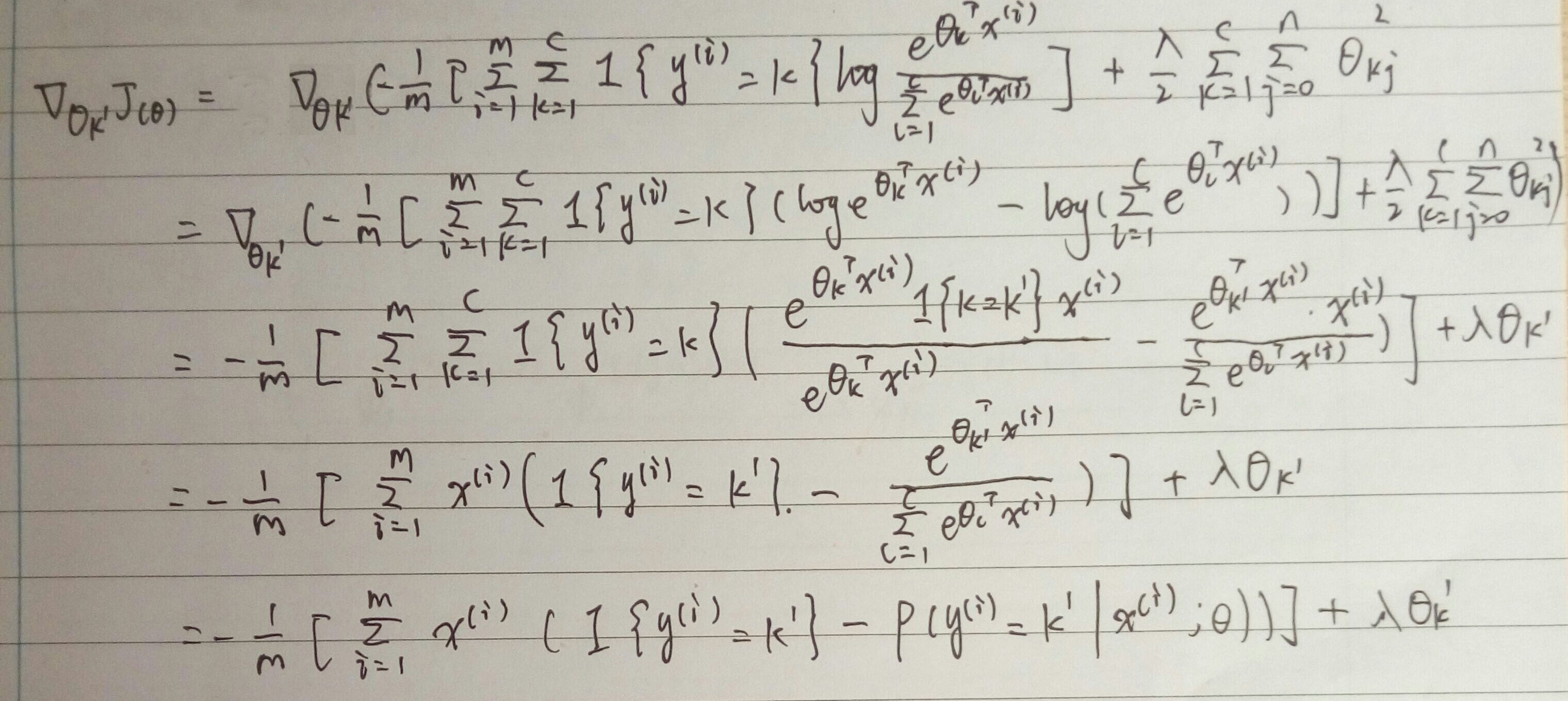














 414
414

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








