局部多项式插值法【LPI】的工作原理

全局多项式插值法可以根据整个表面拟合多项式，而局部多项式插值法可以对位于指定重叠邻域内的多个多项式进行拟合。通过使用大小和形状、邻域数量和部分配置，可以对搜索邻域进行定义。.或者，可以使用探索性趋势面分析参数同步更改带宽、空间条件数（如果已启用）和搜索邻域值。还可以通过优化按钮 优化 基于交叉验证统计信息为 LPI 进行参数优化。

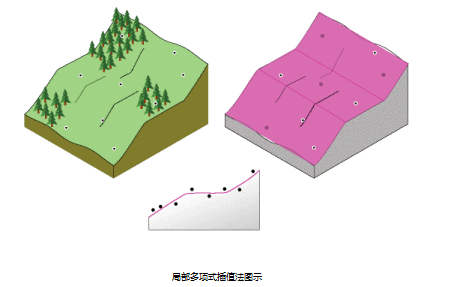
一阶全局多项式可以根据数据对单平面进行拟合；二阶全局多项式可以对包含一个弯曲的表面进行拟合（表面可以表示山谷）；三阶全局多项可以对包含两个弯曲的表面进行拟合；依此类推。但是，当表面具有多种形状（如延绵起伏的地表）时，单个全局多项式将无法很好地拟合。多个多项式平面能够更加准确地体现表面，如下图所示：

另一方面，局部多项式插值法仅使用既定邻域内的点对指定阶数（0 阶、1 阶、2 阶、3 阶，等等）的多项式进行拟合。邻域相互重叠，每次预测所使用值是位于邻域中心的拟合的多项式的值。<