今天博主来稍微介绍一点欧拉函数的知识
欧拉函数
在数论中,对正整数n,欧拉函数是小于n的正整数中与n互质的数的数目(记作φ(n),其中φ(1)=1)
注意,欧拉函数是一种积性函数,它并不是完全积性的,它只满足:对于正整数n的一个算术函数 f(n),且f(1)=1,并当a,b互质时f(ab)=f(a)f(b)
欧拉函数的计算公式
其中p1, p2……pn为x的所有质因数,x是不为0的整数。
欧拉函数的性质
(1) p^k型欧拉函数:
若N是质数p(即N=p), φ(n)= φ(p)=p-p^(k-1)=p-1。
若N是质数p的k次幂(即N=p^k),φ(n)=p^k-p^(k-1)=(p-1)p^(k-1)。
(2)mn型欧拉函数
设n为正整数,以φ(n)表示不超过n且与n互素的正整数的个数,称为n的欧拉函数值。若m,n互质,φ(mn)=(m-1)(n-1)=φ(m)φ(n)。
(3)特殊性质:
若n为奇数时,φ(2n)=φ(n)。
对于任何两个互质的正整数a,n(n>2)有:a^φ(n)≡1 mod n (欧拉定理)
当n=p 且 a与素数p互质(即:gcd(a,p)=1)则上式有: a^(p-1)≡1 mod n (费马小定理)
代码实现
1、直接求解欧拉函数,此种方法因为时间复杂度较高,在竞赛中一般不使用,但是作为对于欧拉函数的理解,我觉得有必要在这里放出
int phi(int n){ //返回φ(n)
int res=n,a=n;
for(int i=2;i*i<=a;i++){
if(a%i==0){
res=res/i*(i-1);//先进行除法是为了防止中间数据的溢出
while(a%i==0) a/=i;
}
}
if(a>1) res=res/a*(a-1);
return res;
} 2、筛法求欧拉函数,此种方法直接预处理了MAXN以内的数所对应的欧拉函数,因为欧拉函数一般与筛素数会同时出现,所以这里放出的代码会将两个筛一起实现
const int MAXN = 10000000;
bool check[MAXN+10];
int phi[MAXN+10];
int prime[MAXN+10];
int tot;
void phi_and_prime_table(int N){
memset(check,false,sizeof(check));
phi[1] = 1;
tot = 0;
for(int i = 2; i <= N; i++){
if( !check[i] ){
prime[tot++] = i;
phi[i] = i-1;
}
for(int j = 0; j < tot; j++){
if(i * prime[j] > N)break;
check[i * prime[j]] = true;
if( i % prime[j] == 0){
phi[i * prime[j]] = phi[i] * prime[j];
break;
}
else{
phi[i * prime[j]] = phi[i] * (prime[j] - 1);
}
}
}
}欧拉函数的应用
求一个数的所有质因子之和:
一个数的所有质因子之和是φ(n)*n/2。
欧拉函数与最大公因数关系的应用:
求GCD(1,n)+GCD(2,n)+……+GCD(n-1,n)
1.建立递推关系,s(n)=s(n-1)+gcd(1,n)+gcd(2,n)+……+gcd(n-1,n);
2.设f(n)=gcd(1,n)+gcd(2,n)+……+gcd(n-1,n)。
其中,gcd(x,n)=i是n的约数(x<n),按照这个约数进行分类。设满足gcd(x,n)=i的有g(n,i)个,则有f(n)=sum(i*g(n,i))。
而gcd(x,n)=i等价于gcd(x/i,n/i)=1,因此g(n,i)等价于φ(n/i)
3.降低时间复杂度。用筛法预处理phi[x]表,再用筛法预处理f(x)->枚举因数,更新其所有倍数求解。
下面贴出代码
typedef long long ll;
const int MAXN = 4000010;
bool check[MAXN+10];
int phi[MAXN+10];
int prime[MAXN+10];
int tot;
void phi_and_prime_table(int N){
memset(check,false,sizeof(check));
phi[1] = 1;
tot = 0;
for(int i = 2; i <= N; i++){
if( !check[i] ){
prime[tot++] = i;
phi[i] = i-1;
}
for(int j = 0; j < tot; j++){
if(i * prime[j] > N)break;
check[i * prime[j]] = true;
if( i % prime[j] == 0){
phi[i * prime[j]] = phi[i] * prime[j];
break;
}
else{
phi[i * prime[j]] = phi[i] * (prime[j] - 1);
}
}
}
}
ll f[MAXN],s[MAXN];
int main(){
phi_and_prime_table(MAXN);
memset(f,0,sizeof(f));
for(int i=1; i<=MAXN; i++)
for(int j=i+i; j<=MAXN; j+=i)
f[j]+=i*phi[j/i];
memset(s,0,sizeof(s));
s[1]=0;
for(int i=2; i<=MAXN; i++)
s[i]=s[i-1]+f[i];
int n;
while(~scanf("%d",&n)&&n){
printf("%lld\n",s[n]);
}
return 0;
}







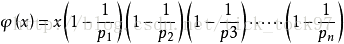













 886
886











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








