前言
最近在看吴军博士的《数学之美》一书,把很多之前没注意到,没用到,甚至不知道怎么用的数学知识和实际问题联系了起来,感觉打开了新世界的大门一样。这本书很多知识点还有技术都是点到为止,并没有深入,所谓师傅领进门,修行在个人吧。所以从本篇开始,博主将对数学之美一书中的一些提到的东西做个总结。不对的地方希望各位看官大佬们多多指正。
在本书第16章《信息指纹及其应用》一文中,介绍到了现在常用的一个伪随机数生成算法,梅森旋转(Mersenne Twister/MT)算法,它的周期长,对于一个k位2进制数,梅森旋转算法可在[0,2^k-1]的范围内生成离散型均匀分布的随机数。
以下内容大多翻译自Wikipedia(中文wiki里的和英文的差的实在太多了……不然我就直接搬运了)
正文
优点
·许可免费,而且对所有它的变体专利免费(除CryptMT外)
·几乎无处不在:它被包含在大多数编程语言和库中
·通过了包括Diehard测试在内的大多数统计随机性测试(除TestU01测试外)
·在应用最广泛的MT19937变体中,周期长达2^19937-1
·在MT19937-32的情况下对1 ≤ k ≤ 623,满足k-分布
·比其他大多数随机数发生算法要快
k-分布
一个周期为P的w位整数的随机序列xi,当满足如下条件时被称为满足v位的k-分布:
假设truncv(x)表示x的前v位形成的数字,并且长度为P的kv位序列:

其中每个可能出现的2^kv组合在一个周期内出现相同的次数(除全0序列出现次数次数比其他序列少1次)
缺点
·需要大量的缓冲器(2.5kib),但在TinyMT版本中修正
·吞吐量中等,但在SFMT版本中修正
·产生的随机数与seed相关,不能用于蒙特卡洛模拟
·由相同的初始序列产生的随机状态几乎相同,但在2002年的更新中对MT算法的初始化进行了改进,使得对于相同的初始序列也能产生不同的随机状态
·非加密安全的,除CryptMT外
算法详细
本算法基于标准(线性)旋转反馈移位寄存器(twisted generalised feedback shift register/TGFSR)产生随机数
算法中用到的变量如下所示:
·w:长度(以bit为单位)
·n:递归长度
·m:周期参数,用作第三阶段的偏移量
·r:低位掩码/低位要提取的位数
·a:旋转矩阵的参数
·f:初始化梅森旋转链所需参数
·b,c:TGFSR的掩码
·s,t:TGFSR的位移量
·u,d,l:额外梅森旋转所需的掩码和位移量
MT19937-32的参数列表如下:
·(w, n, m, r) = (32, 624, 397, 31)
·a = 9908B0DF(16)
·f = 1812433253
·(u, d) = (11, FFFFFFFF16)
·(s, b) = (7, 9D2C568016)
·(t, c) = (15, EFC6000016)
·l = 18
MT19937-64的参数列表如下:
·(w, n, m, r) = (64, 312, 156, 31)
·a = B5026F5AA96619E9(16)
·f = 6364136223846793005
·(u, d) = (29, 555555555555555516)
·(s, b) = (17, 71D67FFFEDA6000016)
·(t, c) = (37, FFF7EEE00000000016)
·l = 43
整个算法分为三个阶段(如图所示):
第一阶段:初始化,获得基础的梅森旋转链;
第二阶段:对于旋转链进行旋转算法;
第三阶段:对于旋转算法所得的结果进行处理;
初始化
首先将传入的seed赋给MT[0]作为初值,然后根据递推式:MT[i] = f × (MT[i-1] ⊕ (MT[i-1] >> (w-2))) + i递推求出梅森旋转链。伪代码如下:
// 由一个seed初始化随机数产生器
function seed_mt(int seed) {
index := n
MT[0] := seed
for i from 1 to (n - 1) {
MT[i] := lowest w bits of (f * (MT[i-1] xor (MT[i-1] >> (w-2))) + i)
}
}对旋转链执行旋转算法
遍历旋转链,对每个MT[i],根据递推式:MT[i] = MT[i+m]⊕((upper_mask(MT[i]) || lower_mask(MT[i+1]))A)进行旋转链处理。
其中,“||”代表连接的意思,即组合MT[i]的高 w-r 位和MT[i+1]的低 r 位,设组合后的数字为x,则xA的运算规则为(x0是最低位):
伪代码为:
lower_mask = (1 << r) - 1
upper_mask = !lower_mask
// 旋转算法处理旋转链
function twist() {
for i from 0 to (n-1) {
int x := (MT[i] & upper_mask)+ (MT[(i+1) mod n] & lower_mask)
int xA := x >> 1
if (x mod 2) != 0 {
// 最低位是1
xA := xA xor a
}
MT[i] := MT[(i + m) mod n] xor xA
}
index := 0
}对旋转算法所得结果进行处理
设x是当前序列的下一个值,y是一个临时中间变量,z是算法的返回值。则处理过程如下:
y := x ⊕ ((x >> u) & d)
y := y ⊕ ((y << s) & b)
y := y ⊕ ((y << t) & c)
z := y ⊕ (y >> l)
伪代码如下:
// 从MT[index]中提取出一个经过处理的值
// 每输出n个数字要执行一次旋转算法,以保证随机性
function extract_number() {
if index >= n {
if index > n {
error "发生器尚未初始化"
}
twist()
}
int x := MT[index]
y := x xor ((x >> u) and d)
y := y xor ((y << s) and b)
y := y xor ((y << t) and c)
z := y xor (y >> l)
index := index + 1
return lowest w bits of (z)
}MT-19937-32实现代码(C语言版)
#include <stdint.h>
// 定义MT19937-32的常数
enum
{
// 假定 W = 32 (此项省略)
N = 624,
M = 397,
R = 31,
A = 0x9908B0DF,
F = 1812433253,
U = 11,
// 假定 D = 0xFFFFFFFF (此项省略)
S = 7,
B = 0x9D2C5680,
T = 15,
C = 0xEFC60000,
L = 18,
MASK_LOWER = (1ull << R) - 1,
MASK_UPPER = (1ull << R)
};
static uint32_t mt[N];
static uint16_t index;
// 根据给定的seed初始化旋转链
void Initialize(const uint32_t seed)
{
uint32_t i;
mt[0] = seed;
for ( i = 1; i < N; i++ )
{
mt[i] = (F * (mt[i - 1] ^ (mt[i - 1] >> 30)) + i);
}
index = N;
}
static void Twist()
{
uint32_t i, x, xA;
for ( i = 0; i < N; i++ )
{
x = (mt[i] & MASK_UPPER) + (mt[(i + 1) % N] & MASK_LOWER);
xA = x >> 1;
if ( x & 0x1 )
{
xA ^= A;
}
mt[i] = mt[(i + M) % N] ^ xA;
}
index = 0;
}
// 产生一个32位随机数
uint32_t ExtractU32()
{
uint32_t y;
int i = index;
if ( index >= N )
{
Twist();
i = index;
}
y = mt[i];
index = i + 1;
y ^= (y >> U);
y ^= (y << S) & B;
y ^= (y << T) & C;
y ^= (y >> L);
return y;
}








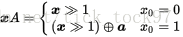
















 6万+
6万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








