Linear Regression/线性回归与正则化（Andrew Ng 机器学习 一 ）

线性回归

用一个线性函数对提供的已知数据进行拟合，最终得到一个线性函数，使这个函数满足我们的要求（如具有最小平方差,随后我们将定义一个代价函数，使这个目标量化），之后我们可以利用这个函数，对给定的输入进行预测（例如，给定房屋面积，我们预测这个房屋的价格）。
如图所示（得到了一条直线）：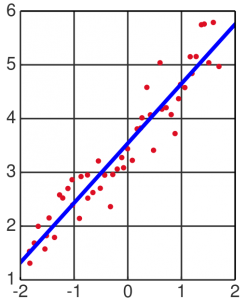
假设我们最终要的得到的假设函数具有如下形式：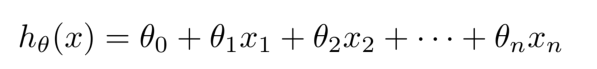
其中，x是我们的输入，theta是我们要求得的参数。

我们的目标是使得此代价函数具有最小值。

为此，我们还需要求得代价函数关于参量theta的导数，即梯度，具有如下形式：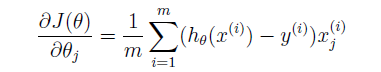
有了这些信息之后，我们就可以用梯度下降算法来求得theta参数。过程如下：

关于正则化

线性回归同样可以采用正则化手段，其主要目的就是防止过拟合。因此解决过拟合问题的一种方法就是正则化。
当采用L1正则化时，则变成了LassoRegresion；当采用L2正则化时，则变成了Ridge Regression；线性回归未采用正则化手段。通常来说，在训练模型时是建议采用正则化手段的，特别是在训练数据的量特别少的时候，若不采用正则化手段，过拟合现象会非常严重。L2正则化相比L1而言会更容易收敛（迭代次数少），但L1可以解决训练数据量小于维度的问题（也就是n元一次方程只有不到n个表达式，这种情况下是多解或无穷解的）。
直接用矩阵的运算求出最佳的theta值。套现成公式，就能求得theta。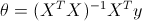
X是矩阵，代表训练集，每一行是一个样本的各特征值。y是个向量，对应每个样本的结果值。

梯度下降与Normal Equation的对比：

Gradient Descent	Normal Equation
自定义alpha	不需要定义alpha
循环Ｎ次才能得到最佳theta值	不需要任何循环操作
特征个数非常大时，也适用	适用于特征个数小于100000时使用
需要feature scaling	不需要feature scaling

---

这里提到Feature Scaling，feature scaling的方法可自定义，常用的有：
1) mean normalization (or standardization)
　 (X - mean(X))/std(X)
2) rescaling
(X - min) / (max - min)

附录（编程答案）

斯坦福大学机器学习week2(Linear Regression)编程习题
* plotData.m

function plotData(x, y)
% ====================== YOUR CODE HERE ======================
figure; % open a new figure window
plot(x, y, '+', 'MarkerSize', 10);
xlabel('Population of City in 10,000s');
ylabel('Profit in $10,000s');
% ============================================================
end

• computeCost.m

function J = computeCost(X, y, theta)
% Initialize some useful values
m = length(y); % number of training examples
% ====================== YOUR CODE HERE ======================
% Instructions: Compute the cost of a particular choice of theta
%               You should set J to the cost.
J = sum((X * theta - y) .^ 2) / (2 * m);
% ==========================================================
end

• gradientDescent.m

function [theta, J_history] = gradientDescent(X, y, theta, alpha, num_iters)
m = length(y); % number of training examples
J_history = zeros(num_iters, 1);
for iter = 1:num_iters
% ====================== YOUR CODE HERE ======================
    theta = theta - alpha * (X' * (X * theta - y)) / m
% ============================================================
% Save the cost J in every iteration    
    J_history(iter) = computeCost(X, y, theta);
end
end

• featureNormalize.m

function [X_norm, mu, sigma] = featureNormalize(X)
% You need to set these values correctly
X_norm = X;
mu = zeros(1, size(X, 2));
sigma = zeros(1, size(X, 2));
% ====================== YOUR CODE HERE ======================
len = length(X);
mu = mean(X);
sigma = std(X);
X_norm = (X - ones(len, 1) * mu) ./ (ones(len, 1) * sigma);
% ============================================================
end

• normalEqn.m

function [theta] = normalEqn(X, y)
theta = zeros(size(X, 2), 1);
% ====================== YOUR CODE HERE ======================
% ---------------------- Sample Solution ----------------------
theta = pinv(X' * X) * X' * y
% ============================================================
end

备注：视频可以在Coursera机器学习课程上观看或下载：https://class.coursera.org/ml