原地址:http://blog.sina.com.cn/s/blog_6dcd52870100yl2v.html
http://zh.wikipedia.org/wiki/%E9%98%BF%E8%BE%BE%E9%A9%AC%E5%8F%98%E6%8D%A2
哈达玛(Hadamard)矩阵是由+1和-1元素构成的正交方阵。所谓正交方阵,指它的任意两行(或两列)都是正交的。把行(或列)看作一个函数,任意两行(或两列)都是正交的 H2n=[Hn Hn;Hn -Hn].在现在的视频编码标准中,阿达马变换多被用来计算SATD(一种视频残差信号大小的衡量)。
变换矩阵
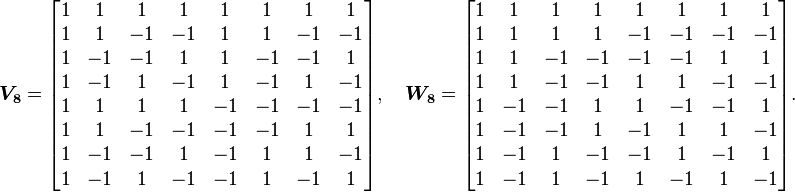
在H.264中使用了4阶和8阶的阿达马变换来计算SATD,其变换矩阵为:
SATD计算方法
当计算4x4块 的SATD时,先使用下面的方法进行二维的阿达马变换:
的SATD时,先使用下面的方法进行二维的阿达马变换:
类似的,当计算8x8块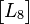 的SATD时,先使用下面的方法进行二维的Hadamard变换:
的SATD时,先使用下面的方法进行二维的Hadamard变换:
构建阿达马变换
阿达马变换转换主要型式为 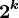 点的转换矩阵,其最小单位矩阵为 2x2 的阿达马变换矩阵,以下分别为二点、四点与如何产生
点的转换矩阵,其最小单位矩阵为 2x2 的阿达马变换矩阵,以下分别为二点、四点与如何产生 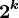 点的阿达马变换转换步骤。
点的阿达马变换转换步骤。
- 二点阿达马变换转换:

- 四点阿达马变换转换:
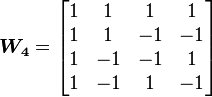
- 产生
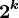 点阿达马变换的步骤:
点阿达马变换的步骤:
步骤一: 
步骤二: 根据正负号次序 (Sign change,正负号改变次数) 将矩阵 (Matrix) 内的列向量座顺序上的重新排列。

范例

优缺点比较
优点
- 仅需实数运算 (Real operation) 。
- 不需乘法运算 (No multiplication) ,仅有加减法运算。
- 有部分性质类似于离散傅立叶变换 (Discrete fourier transform) 。
- 顺向转换 (Forward transform) 与反向转换 (Inverse transform ) 型式为相似式。
![\begin{cases} \begin{matrix} F\left[ m \right] &=& \sum_{n=0}^{N-1} W\left[ {m, n} \right] f\left[ n \right] & & (\mbox{Forward Type}) \\ f\left[ n \right] &=& \left( \frac{1}{N} \right) \sum_{n=0}^{N-1} W\left[ {m, n} \right]F\left[ m \right] & &(\mbox{Inverse Type}) \end{matrix} \end{cases},](http://upload.wikimedia.org/math/8/6/6/866793c1de8c78aec8b6b08f454f46dd.png)
其中 ![F\left[ n \right]](http://upload.wikimedia.org/math/4/f/9/4f9005959f0e0ce3c04d04644486a4ab.png) 与
与 ![f\left[ n \right]](http://upload.wikimedia.org/math/0/3/f/03f2bb08bedc040597e4de002eacc734.png) 分别都为行向量 (Column vector) 。
分别都为行向量 (Column vector) 。
缺点
Hadamard变换
for (j=0;j<16;j)
//计算当前宏块残差块
第二次一维Hadamard变换
}
}
}
以上是源程序里的一段,intra_16*16并不是计算SAD值,而是计算SATD。
其中M1中放的是宏块的残差,M0也是,不过为了下面计算HADAMARD变换方便,他表示成M0[4][4][4][4]的形式,前2个[4][4]表示8X8块坐标,后2个[4][4]表示一个8X8里的4X4块坐标。
程序先对残差进行HADAMARD变换,然后把所有的DC分量提出来,再对DC分量做HADAMARD变换,
最后得到的是SATD。
有两点不明白,谁知道的解释一下:
1 在提取DC分量时为什么要除以4?
2 最后的best_intra_sad2 为什么要除以2?
这主要是由于SATD变换不是归一化矩阵,变换后的系数值幅值增加,因此要相应的/2和/4
hadamard 变换本身就有一个 /2 的操作,因此每次变换都要对所有系数进行 /2。而 find_sad_16x16 函数执行了两次 hadamard 变换:首先对 256 个系数进行一次,其次对所有 DC 系数再做一次,因此对 DC 系数应该 /4,而对 AC 系数应该 /2。find_sad_16x16 函数中的:M4[ i ][j]=M0[0][ i ][0][j]/4;就是对 DC 系数 /4,而最后的:best_intra_sad2 = best_intra_sad2/2;可以认为是对 AC 系数的变相 /2。但这里相当于是对所有系数 /2,所以 DC 系数多了一次 /2。这个多的一次就不知道原因了。
264乐园群里探讨过这个问题。对于hadamard变换的/2已经有了结论。但是对DC系数多除的那一次2,目前尚未找到根据。
4阶hadamard变换的定义式本身就是包含了这个/2的。可以见http://en.wikipedia.org/wiki/Hadamard_transform。这里再多解释一点
假设hadamard变换没有/2, 变换矩阵为:
1
1 -1
1
1 -1 -1 1
这时对一个列向量v = (1, 1, 1, 1)'做变换,即用变换矩阵左乘列向量v,得到的变换后向量v' = (4, 0, 0, 0)'。
现在观察v和v',在欧氏空间中,对一个向量的“大小”的衡量就是其长度,通过计算内积得到。那么
len(v)
len(v') = sqrt( 4^2 + 0^2 + 0^2 + 0^2) = 4
由此可见如果没有那个/2,变换前后,该向量的长度发生了变化。这样的变换是违背正交变换的定义的。
所以,作为正交变换的hadamard变换,必须要有这个/2的归一化。
A:推而广之,整数 DCT 变换在变换前后向量的长度也发生了变化,为什么没有除以 2 呢?
DCT变换(非整数)也是归一化的整数变换也是正交变换,所以也一定会满足归一化的。firstime是不是忘记把scaling matrix考虑进来了啊。
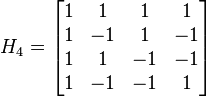
按照毕厚杰书上 113 页,变换矩阵为公式 6.15(这个时候 scaling matrix 还没分离出来吧?):
a
b
a -a -a
c -b
其中 a = 1/2,b = (2/5)^0.5。这个矩阵对列向量v = (1, 1, 1, 1)'做变换前后的向量长度并不相等啊。
才发现毕厚杰书上的DCT变换矩阵是错的。。。。第二行第四列应该是-b
应该是
a
b
a -a -a
c -b









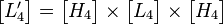
 所有系数
所有系数
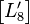 所有系数
所有系数












 227
227











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








