目录
1、Hadamard积
考虑两个矩阵之间的直接乘积。
定义:矩阵
与
矩阵
的Hadamard积记作
,它仍然是一个
矩阵,定义为
Hadamard积也称为Schur积或者对应元素乘积。矩阵Hadamard积的一个重要结果是下面的Hadamard积定理。
定理:若矩阵是正定(或半正定)的,则它们的Hadamard积
也是正定(或半正定)的。
推论(Fejer定理):令A是一个矩阵,则A是半正定当且仅当
对所有
半正定矩阵B成立。
下面两个定理描述了矩阵的Hadamard积与迹之间的关系:
定理:令A,B,C为矩阵,并且
为
求和向量,
,其中,
,则
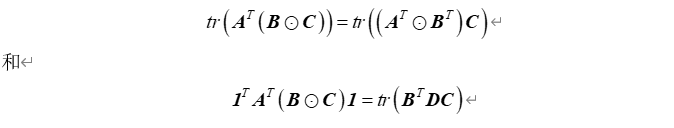
定理:令A,B为正方矩阵,并且为
求和向量,假设M是一个
对角矩阵
,而
为
向量,则有
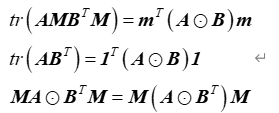
Hadamard积具有以下性质:
(1) 若A,B均为矩阵,则
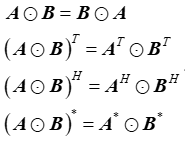
(2) 任何一个矩阵A与
零矩阵
的Hadamard积等于
零矩阵,即
。
(3) 若c为常数,则
![]()
(4) 矩阵与单位矩阵
的Hadamard积为
对角矩阵,即
![]()
(5) 若A,B,C,D均为矩阵,则
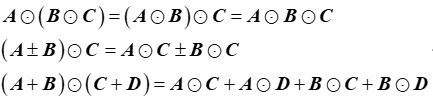
(6) 若A,C为矩阵,并且B,D为
矩阵,则
![]()
(7) 若A,B,C为矩阵,则
![]()
(8) 若A,B,D为矩阵,则
![]()
(9) 若矩阵A,B是正定的(或半正定)的,则它们的Hadamard积
也是正定(或半正定)的。
tip:关于Hadamard积的具体证明可自行查阅张贤达的《矩阵分析与应用》。
2、Kronecker积
Kronecker积是表示矩阵特殊乘积的一种简洁数字符号。一个矩阵A和一个
矩阵B的Kronecker积记作
,它是一个
矩阵。
Kronecker积也称直积(direct product)或者张量积(tensor product)。
定义(右Kronecker积):矩阵A和
矩阵B的右Kronecker积
定义为

更具体可以表示为

定义(左Kronecker积):矩阵A和
矩阵B的左Kronecker积
定义为
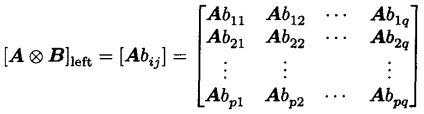
若矩阵,则
![]()
如下面定理所述,向量化算子这一性质公式可以推广为矩阵乘积的向量化公式。
定理:令,则
![]()
Kronecker积具有以下性质:
(1) 对于矩阵和
,一般有
。
(2) 任意矩阵与零矩阵的Kronecker积等于零矩阵,即
(3) 若和
为常数,则
![]()
(4) 对于矩阵,有
![]()
(5) 对于矩阵,有

(6) 若矩阵A和B分别有广义逆矩阵和
,则
![]()
特别地,若A和B是可逆的正方矩阵,则
![]()
(7) 对于矩阵,有
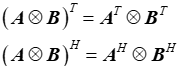
(8) 对于矩阵,有
![]()
(9) 若A是矩阵,B是
矩阵,则
![]()
(10) 若A是矩阵,B是
矩阵,则
(11) 对于矩阵,有
![]()
更一般地,有
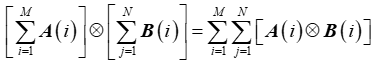
(12) 对于矩阵,有
![]()
(13) 若是矩阵A与特征值
对应的特征向量,
是矩阵B与特征值
对应的特征向量,则
是矩阵
与特征值
对应的特征向量,也是与特征值
对应的特征向量。
(14) 对于矩阵,有
![]()
(15) 对于矩阵,有
![]()
更一般地,有
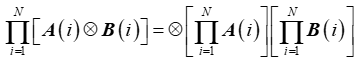
和
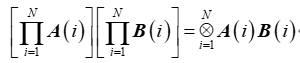
(16) 对于矩阵,有
(17) 作为性质(15)的特例,若和
,则
![]()
式中,为块对角矩阵(对右Kronecker积)或稀疏矩阵(对左Kronecker积),而
为稀疏矩阵(对右Kronecker积)或块对角矩阵(对左Kronecker积)。
tip:关于Kronecker积的具体证明可自行查阅张贤达的《矩阵分析与应用》。






















 6056
6056

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








