引言
SVM的学习问题可以转化为下面的对偶问题:
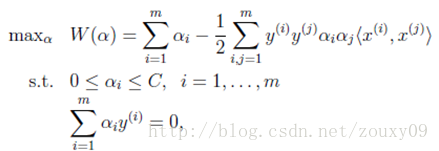
需要满足的KKT条件为:
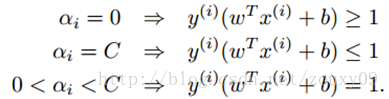
(PS:实际上以上的三个公式是我们根据KKT条件得到的 )
也就是说找到一组αi可以满足上面的这些条件的就是该目标的一个最优解。所以我们的优化目标是找到一组最优的αi*。一旦求出这些αi*,就很容易计算出权重向量w*和b,并得到分隔超平面了。
这是个凸二次规划问题,它具有全局最优解,一般可以通过现有的工具来优化。但当训练样本非常多的时候,这些优化算法往往非常耗时低效,以致无法使用。从SVM提出到现在,也出现了很多优化训练的方法。其中,非常出名的一个是1982年由Microsoft Research的John C. Platt在论文《Sequential Minimal Optimization: A Fast Algorithm for TrainingSupport Vector Machines》中提出的Sequential Minimal Optimization序列最小化优化算法,简称SMO算法。SMO算法的思想很简单,它将大优化的问题分解成多个小优化的问题。这些小问题往往比较容易求解,并且对他们进行顺序求解的结果与将他们作为整体来求解的结果完全一致。在结果完全一致的同时,SMO的求解时间短很多。在深入SMO算法之前,我们先来了解下坐标下降这个算法,SMO其实基于这种简单的思想的。
坐标下降(上升)法
假设要求解下面的优化问题:
在这里,我们需要求解m个变量αi,一般来说是通过梯度下降(这里是求最大值,所以应该叫上升)等算法每一次迭代对 所有m个变量αi也就是α向量进行一次性优化。(解释一下:注意这里说的是一个向量的所有分量,注意不要和梯度下降与随机梯度下降中的一个样本/所有样本混淆)。通过误差每次迭代调整α向量中每个元素的值。而坐标上升法(坐标上升与坐标下降可以看做是一对,坐标上升是用来求解max最优化问题,坐标下降用于求min最优化问题)的思想是每次迭代只 调整一个变量αi的值,其他变量的值在这次迭代中固定不变。(这里指的是一个变量中的一个分量)。

最里面语句的意思是固定除αi之外的所有αj(i不等于j),这时W可看作只是关于αi的函数,那么直接对αi求导优化即可。 这里我们进行最大化求导的顺序i是从1到m,可以通过更改优化顺序来使W能够更快地增加并收敛。如果W在内循环中能够很快地达到最优,那么坐标上升法会是一个很高效的求极值方法。
用个二维的例子来说明下坐标下降法:我们需要寻找f(x,y)=x2+xy+y2的最小值处的(x*, y*),也就是下图的F*点的地方.
假设我们初始的点是A(图是函数投影到xoy平面的等高线图,颜色越深值越小),我们需要达到F*的地方。那最快的方法就是图中黄色线的路径,一次性就到达了,其实这个是牛顿优化法,但如果是高维的话,这个方法就不太高效了(因为需要求解矩阵的逆,这个不在这里讨论)。我们也可以按照红色所指示的路径来走。从A开始,先固定x,沿着y轴往让f(x, y)值减小的方向走到B点,然后固定y,沿着x轴往让f(x, y)值减小的方向走到C点,不断循环,直到到达F*。反正每次只要我们都往让f(x, y)值小的地方走就行了,这样脚踏实地,一步步走,每一步都使f(x, y)慢慢变小,总有一天,皇天不负有心人的。到达F*也是时间问题。到这里你可能会说,这红色线比黄色线贫富差距也太严重了吧。因为这里是二维的简单的情况嘛。如果是高维的情况,而且目标函数很复杂的话,再加上样本集很多,那么在梯度下降中,目标函数对所有αi求梯度或者在牛顿法中对矩阵求逆,都是很耗时的。这时候,如果W只对单个αi优化很快的时候,坐标下降法可能会更加高效。
SMO算法
SMO算法与坐标下降(上升)法的思想差不多,不同的是,SMO算法是一次迭代优化两个α而不是一个。为什么要优化两个呢?
SVM的优化问题为:

在这个优化问题中存在一个约束条件:
假设我们首先固定除α1以外的所有参数,然后在α1上求极值。但需要注意的是,因为如果固定α1以外的所有参数,由上面这个约束条件可以知道,α1将不再是变量(可以由其他值推出),因为我们可以计算出来:
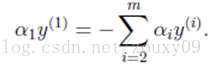
因此,我们需要一次选取两个参数做优化,比如αi和αj,此时αi可以由αj和其他参数表示出来。这样回代入W中,W就只是关于αj的函数了,这时候就可以只对αj进行优化了。在这里就是对αj进行求导,令导数为0就可以解出这个时候最优的αj了。然后也可以得到αi。这就是一次的迭代过程,一次迭代只调整两个拉格朗日乘子αi和αj。SMO之所以高效就是因为在固定其他参数后,对一个参数优化过程很高效(对一个参数的优化可以通过解析求解,而不是迭代。虽然对一个参数的一次最小优化不可能保证其结果就是所优化的拉格朗日乘子的最终结果,但会使目标函数向极小值迈进一步,这样对所有的乘子做最小优化,直到所有满足KKT条件时,目标函数达到最小)。
所以,SMO的优化过程为:
重复以下三步,直至收敛:
1、选择两个拉格朗日乘子αi和αj;
2、固定其他拉格朗日乘子αk(k不等于i和j),只对αi和αj优化,将αi表示成有关αj和αk(k不等于i和j)的式子,则最终w(α)只是有关αj的式子,从而对αj求导,得到优化后的αj,再解出αi;
3、根据优化后的αi和αj,更新截距b的值;
那训练里面这两三步骤到底是怎么实现的,需要考虑什么呢?下面我们来具体分析下:
(1)选择αi和αj—理论:
第一个变量αi的选择
我们现在是每次迭代都优化目标函数的两个拉格朗日乘子αi和αj,然后其他的拉格朗日乘子保持固定。如果有N个训练样本,我们就有N个拉格朗日乘子需要优化,但每次我们只挑两个进行优化,我们就有N(N-1)种选择。那到底我们要选择哪对αi和αj呢?选择哪对才好呢?想想我们的目标是什么?我们希望把所有违法KKT条件的样本都纠正回来,因为如果所有样本都满足KKT条件的话,我们的优化就完成了。那就很直观了,哪个害群之马最严重,我们得先对他进行思想教育,让他尽早回归正途。OK,那我们选择的第一个变量αi就选违法KKT条件最严重的那一个。
第二个变量αj的选择
我们是希望快点找到最优的N个拉格朗日乘子,使得代价函数最大,换句话说,要最快的找到代价函数最大值的地方对应的N个拉格朗日乘子。这样我们的训练时间才会短。每次迭代中,哪对αi和αj可以让我更快的达到代价函数值最大的地方,我们就选他们。或者说,走完这一步,选这对αi和αj代价函数值增加的值最多,比选择其他所有αi和αj的结合中都多。这样我们才可以更快的接近代价函数的最大值,也就是达到优化的目标了。再例如,下图,我们要从A点走到B点,按蓝色的路线走c2方向的时候,一跨一大步,按红色的路线走c1方向的时候,只能是人类的一小步。所以,蓝色路线走两步就迈进了成功之门,而红色的路线,人生曲折,好像成功遥遥无期一样,故曰,选择比努力更重要!

其实就一句话:为什么每次迭代都要选择最好的αi和αj,就是为了更快的收敛!
(2)选择αi和αj—实践
那实践中每次迭代到底要怎样选αi和αj呢?这有个很好听的名字叫启发式选择,主要思想是先选择最有可能需要优化(也就是违反KKT条件最严重)的αi,再针对这样的αi选择最有可能取得较大修正步长的αj。具体是以下两个过程:
1)第一个变量αi的选择:
SMO称选择第一个变量的过程为外层循环。外层训练在训练样本中选取违法KKT条件最严重的样本点。并将其对应的变量作为第一个变量。具体的,检验训练样本(xi, yi)是否满足KKT条件,也就是:

该检验是在ε范围内进行的。在检验过程中,外层循环首先遍历所有满足条件
优先选择遍历间隔边界上数据样本,因为间隔边界上的数据样本更有可能需要调整,间隔边界之外的数据样本常常不能得到进一步调整而留在间隔边界之外。由于大部分数据样本都很明显不可能是支持向量,因此对应的α乘子一旦取得零值就无需再调整。遍历间隔边界上数据样本并选出他们当中违反KKT 条件为止。当某一次遍历发现没有间隔边界数据样本得到调整时(即没有间隔边界数据样本违反KKT条件),遍历所有数据样本,以检验是否整个集合都满足KKT条件。如果整个集合的检验中又有数据样本被进一步进化,则有必要再遍历间隔边界上的数据样本。这样,不停地在遍历所有数据样本和遍历间隔边界数据样本之间切换,直到整个样本集合都满足KKT条件为止。以上用KKT条件对数据样本所做的检验都以达到一定精度ε就可以停止为条件。如果要求十分精确的输出算法,则往往不能很快收敛。
对整个数据集的遍历扫描相当容易,而实现对间隔边界αi的扫描时,首先需要将所有间隔边界样本的αi值(也就是满足0<αi
2)第二个变量αj的选择:
在选择第一个αi后,算法会通过一个内循环来选择第二个αj值。因为第二个乘子的迭代步长大致正比于|Ei-Ej|,所以我们需要选择能够最大化|Ei-Ej|的第二个乘子(选择最大化迭代步长的第二个乘子)。在这里,为了节省计算时间,我们建立一个全局的缓存用于保存所有样本的误差值,而不用每次选择的时候就重新计算。我们从中选择使得步长最大或者|Ei-Ej|最大的αj。
(3)优化αi和αj:
选择这两个拉格朗日乘子之后,我们需要先计算这些参数的约束值,然后再求解这个约束最大化的问题:
首先,我们需要给αj找到边界L<=αj<=H,以保证αj满足0<=αj<=C的约束。这意味着αj必须落入这个盒子中。由于只有两个变量(αi, αj),约束可以用二维空间中的图形来表示,如下图:
不等式约束使得(αi,αj)在盒子[0, C]x[0, C]内,等式约束使得(αi, αj)在平行于盒子[0, C]x[0, C]的对角线的直线上。因此要求的是目标函数在一条平行于对角线的线段上的最优值。这使得两个变量的最优化问题成为实质的单变量的最优化问题。由图可以得到,αj的上下界可以通过下面的方法得到:
我们优化的时候,αj必须要满足上面这个约束。也就是说上面是αj的可行域。然后我们开始寻找αj,使得目标函数最大化。通过推导得到αj的更新公式如下:
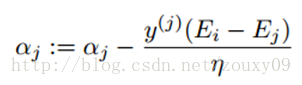
这里Ek可以看做对第k个样本,SVM的输出与期待输出,也就是样本标签的误差。
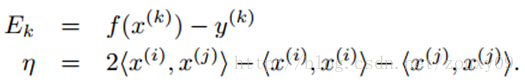
而η实际上是度量两个样本i和j的相似性的。在计算η的时候,我们需要使用核函数,那么就可以用核函数来取代上面的内积。
得到新的αj后,我们需要保证它处于边界内。换句话说,如果这个优化后的值跑出了边界L和H,我们就需要简单的裁剪,将αj收回这个范围:
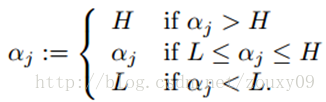
最后,得到优化的αj后,我们需要用它来计算αi:
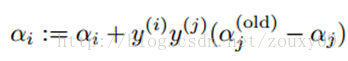
到这里,αi和αj的优化就完成了.
(4)计算阈值b
先摆出积分公式:


SMO的优化问题为(7.101)~(7.103)


(5)凸优化问题的终止条件
SMO算法的基本思路是:如果所有变量都满足此最优化问题的KKT条件,那么这个最优化问题的解就得到了。因为KKT条件是该最优化问题的充分必要条件,所以我们可以监视原问题的KKT条件,如果有样本违反了KKT条件,我们要根据具体的调整策略,优化问题。所以,如果所有的样本都满足KKT条件,那么就表示迭代结束了。但是由于KKT条件本身是比较苛刻的,所以也需要设定一个容忍值,即所有样本在容忍值范围内满足KKT条件,则认为训练可以结束;当然了,对于对偶问题的凸优化还有其他终止条件。
代码实现
代码的实现还是比较复杂的,由于平时时间比较紧张,在此我不贴代码,需要的的同学可以参考:
代码1
代码2,本节大部分内容来在本博文,感谢博主的分享
#_*_ encoding:utf-8 _*_
#sklearn中的SVM算法
import numpy as np
from sklearn import svm
from sklearn.cross_validation import train_test_split
import matplotlib.pyplot as plt
data=[]
labels=[]
with open('data\\1.txt') as ifile:
for line in ifile:
tokens=line.strip().split(' ')
data.append([float(tk)for tk in tokens[:-1]])
labels.append(tokens[-1])
x=np.array(data)
labels=np.array(labels)
y=np.zeros(labels.shape)
y[labels=='fat']=1
x_train,x_test,y_train,y_test=train_test_split(x,y,test_size=0.2)
h=0.2
#画图实现
x_min,x_max=x_train[:,0].min()-0.1,x_train[:,0].max()+0.1
y_min,y_max=x_train[:,1].min()-1,x_train[:,1].max()+1
xx,yy=np.meshgrid(np.arange(x_min,x_max,h),
np.arange(y_min,y_max,h))
'''''SVM'''
titles=['LinearSVC(linear kernel)',
'SVC with polynomial(degree 3 )kernel',
'SVC with RBF kernel',
'SVC with Sigmod kernel']
clf_linear=svm.SVC(kernel='linear').fit(x,y)
#或者clf_linear=svm.LinearSVC().fit(x,y)
clf_poly=svm.SVC(kernel='poly',degree=3).fit(x,y)
clf_rbf=svm.SVC(kernel='rbf').fit(x,y)
clf_sigmod=svm.SVC(kernel='sigmoid').fit(x,y)
for i,clf in enumerate((clf_linear,clf_poly,clf_rbf,clf_sigmod)):
answer=clf.predict(np.c_[xx.ravel(), yy.ravel()])
print clf
plt.subplot(2,2,i+1)
plt.subplots_adjust(wspace=0.4,hspace=0.4)
#put the result into a color plot
z=answer.reshape(xx.shape)
plt.contourf(xx,yy,z,cmap=plt.cm.Paired,alpha=0.8)
# Plot also the training points
plt.scatter(x[:,0], x[:,1], c=y, cmap=plt.cm.Paired)
plt.xlabel(u'hight')
plt.ylabel(u'weight')
plt.xlim(xx.min(), xx.max())
plt.ylim(yy.min(), yy.max())
plt.title(titles[i])
plt.show()实验结果:
在本实验中表现比较好的是:线性核和多项式核,表现最不好的是sigmoid kernel。
<完>
所谓的不平凡就是平凡的N次幂。
-------By Ada










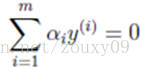























 4万+
4万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










