deeplearning系列（四）主成分分析与白化

1. 主成分分析数学背景

白化是一种常见的数据预处理步骤，而主成分分析（PCA）是实现白化的重要一步。

假设我们有数据集$\{x^{(1)},...x^{(m)}\}$，且这些数据经过了处理，每个维度具有0均值和相同的方差，如下图所示。

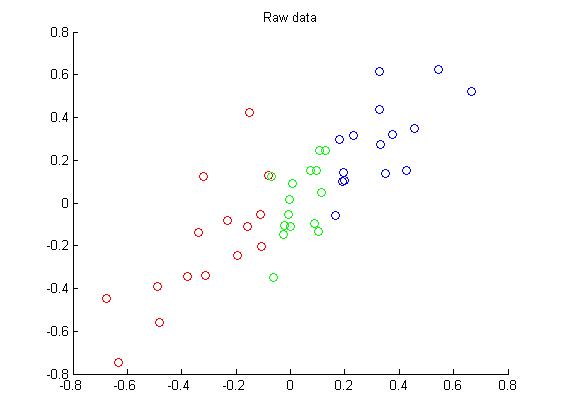
通常数据中存在冗余，以上图为例，数据可以投影到一个方向上，这样数据可以由二维变成一维的，减少数据冗余。

PCA即是这样的一种算法，通过寻找一个低维空间来映射数据。首先要计算协方差矩阵：

$$\Sigma = \frac{1}{m}\sum\limits_{i = 1}^m {({x^{(i)}})} {({x^{(i)}})^T}$$
然后求协方差矩阵的特征向量和特征值：
$$U = [{u_1},...{u_n}]，\lambda=[\lambda_1,...\lambda_n]$$
其中特征值的大小满足关系： $\lambda_1>\lambda_2>...>\lambda_n$，则 $u_1$称为x的第一主轴， $y_1=u_1'x$称为x的第一主成分，以此类推， $u_n$称为x的第n主轴， $y_n=u_n'x$称为x的第n主成分。

2. 旋转数据

旋转后的数据，可以表示为：

$$y=U^Tx$$
matlab代码为：

sigma = x * x' / size(x, 2);
[u,s,v] = svd(sigma);
y = u'*x;

上面数据集旋转后的结果为：

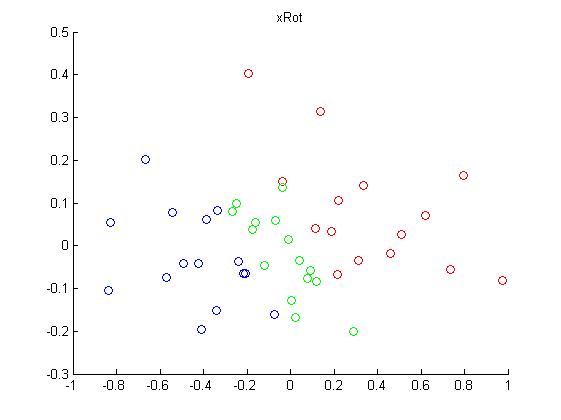
3. 数据降维

在n个特征维度中，经PCA降维后将维度减至k维，降维后的数据可以表示为：

$${x_{rot}} = {[{u_1},{u_2},...{u_k}]^T}x$$
从压缩后的数据还原原始数据，可以表示为：

$${x_{new}} = U{[{u_1},{u_2},...{u_k},0,...,0]^T}x$$
matlab代码如下：

k = 1; % Use k = 1 and project the data     onto the first eigenbasis
xHat = zeros(size(x));
xRot = zeros(size(x));
xRot(1:k,:) = u(:,1:k)' * x;
xHat = u * xRot;

实验结果为：

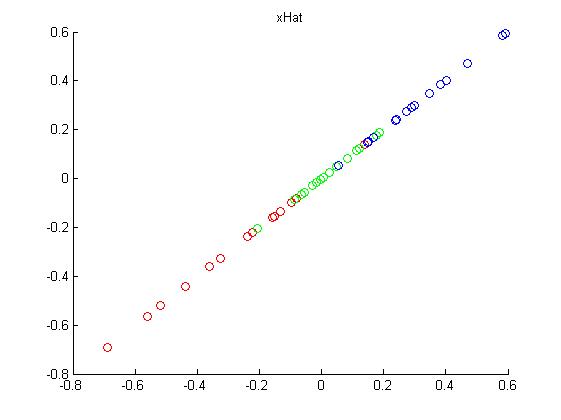
4. PCA白化

对于有些数据集来说，不同特征之间有很强的相关性，比如图像像素之间是有关联的，白化的目的是去除原始特征数据之间的相关性，降低数据的冗余。我们希望经过白化处理后，数据之间具有这样的性质：

1. 特征之间相关性较低；
2. 所有的特征维度具有相同的方差。

由PCA的原理知，经PCA转换后的数据特征之间已没有了相关性，现在仅需要满足第二个条件，统一不同特征之间的方差。
转换后数据的协方差矩阵为：$diag\{\lambda_1,...,\lambda_n\}$。所以仅需要将转换后的每个特征维度乘以$1/\sqrt{\lambda_i}$，因为可能存在特征值$\lambda_i$接近于0的情况，$1/\sqrt{\lambda_i}$此时过大，乘以该数值后会产生数据上溢，在实践中，使用正则化解决这个问题，即给每个特征值加上一个很小的常数$\epsilon$:

$${x_{PCAwhite,i}} = \frac{{{y_i}}}{{\sqrt {{\lambda _i}+\epsilon} }}$$
matlab代码为：

epsilon = 1e-5;
xPCAWhite = zeros(size(x)); 
xRot = u'*x;
xPCAWhite = diag(1./sqrt(diag(s)+epsilon))*xRot;

实验结果：

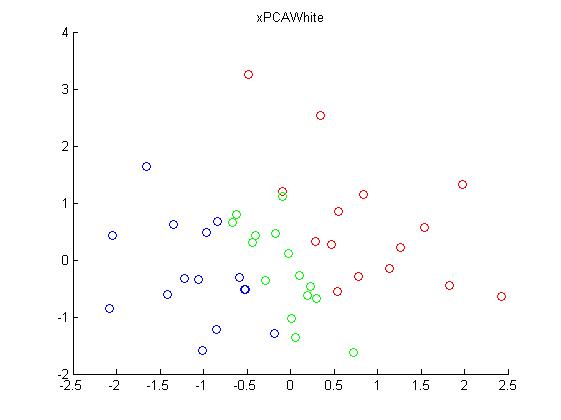
5. ZCA白化

由白化的定义知，所谓白化，即使转换后的数据协方差矩阵为单位矩阵，可以证明，对任意的正交矩阵R，即满足：$R{R^T} = {R^T}R = I$，则$R{x_{PCAwhite}}$仍具有单位协方差。在ZCA白化中，令$R=U$,可得ZCA白化结果为：

$${x_{ZCAwhite}} = U{x_{PCAwhite}}$$
matlab代码为：

xZCAWhite = zeros(size(x)); 
xZCAWhite = u * diag(1./sqrt(diag(s) + epsilon)) * u' * x;

实验结果为：

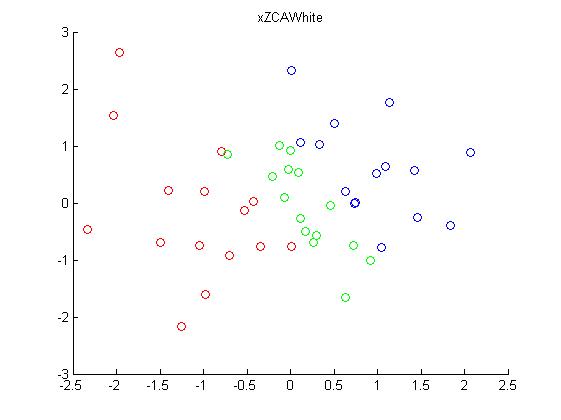
参考资料：
1.http://ufldl.stanford.edu/wiki/index.php/UFLDL_Tutorial