deeplearning系列（二）自编码神经网络

1. Pre_training

神经网络算法通过反向传播（back propogation）求得目标函数关于参数的偏导数（或者称梯度值），然后使用梯度下降法（例如SGD）或者拟牛顿法（例如L-BFGS）等优化算法求得使目标函数最小化时的参数取值。
由于目标函数非凸的，同时由于深度网络参数之多，又因为反向传播对初始化的参数十分敏感，如果参数初始值选择的不好，很容易使目标函数的求解陷入很差的局部最优解。为了解决这个困难的最佳化问题，提出了pre_training 的方案，即通过pre_training技术使预训练得到的参数作为反向传播的起始点。这样可以使反向传播的初始搜索点放在一个比较好的位置，从而保证优化算法可以收敛到一个比较好的局部最优解。

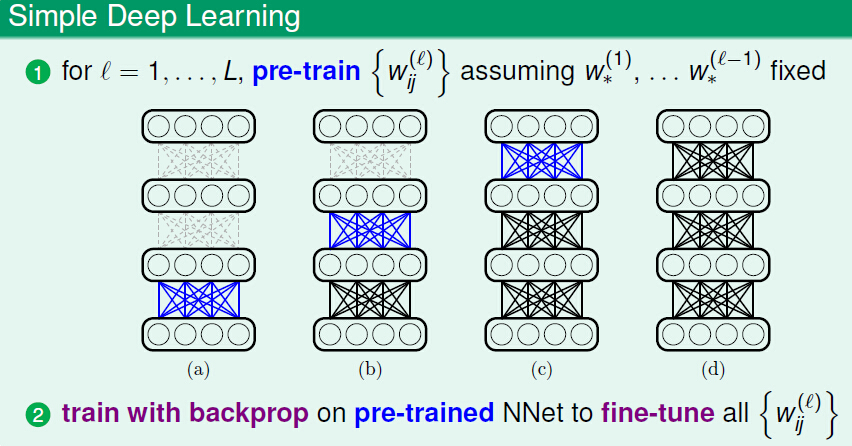
上图展示了一个简单的pre_training的流程图，首先通过逐层pre_training得到每层的参数，然后使用反向传播来微调（fine-tune）这些预训练的参数值。

2. 自编码神经网络

通过神经网络学习的权重参数$W^{(l)}$的物理意义是什么？在神经网络的架构下，权重参数代表了如何进行特征转换，也就是转换输入特征的表现形式，也称为编码（encoding）。pre_training的目的就是学习这些权重参数的，那么怎样定义学习到的参数的好坏呢？
好的权重可以：

1. 以更精炼的形式（特征维数减少）保存前面一层的信息；
2. 同时尽可能少的丢失上一层的信息（也称为information-preserving encoding）；
3. 使用转换后的特征还可以很容易地重构出原始的特征。

自编码神经网络（Autoencoder）即是一种可以满足这些要求的pre_training技术。它是一种无监督学习算法，使用反向传播，使目标函数的输出等于输入值。下图是一个示例。

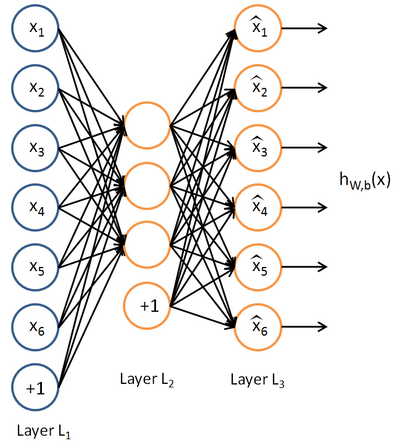
自编码神经网络试图逼近这样的一个恒等函数：$h_{W,b}(x)=x$。使得神经网络的输出等于输入，这样隐藏层可以看做对输入的压缩编码，使用压缩编码后的特征可以重构出原始特征。

3. 稀疏约束

和包含一个隐藏层的普通神经网络相比，自编码神经网络除了满足输出等于输入的要求外，还可以加入其它的要求，比如稀疏性约束。
稀疏约束的一种方式可以表示为：激活函数为sigmoid时，神经元输出接近于1时可以看做该神经元被激活，输出接近于0时看做被抑制。
我们用$a_j^{(2)}$表示隐藏神经元$j$的激活度，则激活度在训练集上的平均值：

$${\hat \rho _j} = \frac{1}{m}\sum\limits_{i = 1}^m {a_j^{(2)}({x^{(i)}})}$$
表示隐藏神经元 $j$的 平均激活度。然后施加稀疏限制：

$${\hat \rho _j} = \rho$$
其中， $\rho$为稀疏性参数，是一个接近于0的值，比如0.05。为了实现这一限制，在目标函数中添加另一个惩罚项，从而使隐藏神经元的激活值在一个接近于 $\rho$的适当范围内。隐藏项选择相对熵的形式：