说明:本文基本上是“整理”性质,致谢文末的参考文献。从Trie树(字典树)谈到后缀树
引言
常关注本blog的读者朋友想必看过此篇文章:从B树、B+树、B*树谈到R 树,这次,咱们来讲另外两种树:Tire树与后缀树。不过,在此之前,先来看两个问题。
第一个问题: 一个文本文件,大约有一万行,每行一个词,要求统计出其中最频繁出现的前10个词,请给出思想,给出时间复杂度分析。
之前在此文:海量数据处理面试题集锦与Bit-map详解中给出的参考答案:用trie树统计每个词出现的次数,时间复杂度是O(n*le)(le表示单词的平均长度),然后是找出出现最频繁的前10个词。也可以用堆来实现(具体的操作可参考第三章、寻找最小的k个数),时间复杂度是O(n*lg10)。所以总的时间复杂度,是O(n*le)与O(n*lg10)中较大的哪一个。
第二个问题:找出给定字符串里的最长回文。例子:输入XMADAMYX。则输出MADAM。这道题的流行解法是用后缀树(Suffix Tree),但其用途远不止如此,它能高效解决一大票复杂的字符串编程问题(当然,它有它的弱点,如算法实现复杂以及空间开销大),概括如下:
- 查询字符串S是否包含子串S1。主要思想是:如果S包含S1,那么S1必定是S的某个后缀的前缀;又因为S的后缀树包含了所有的后缀,所以只需对S的后缀树使用和Trie相同的查找方法查找S1即可(使用后缀树实现的复杂度同流行的KMP算法的复杂度相当)。
- 找出字符串S的最长重复子串S1。比如abcdabcefda里abc同da都重复出现,而最长重复子串是abc。
- 找出字符串S1同S2的最长公共子串。注意最长公共子串(Longest CommonSubstring)和最长公共子序列(LongestCommon Subsequence, LCS)的区别:子串(Substring)是串的一个连续的部分,子序列(Subsequence)则是从不改变序列的顺序,而从序列中去掉任意的元素而获得的新序列;更简略地说,前者(子串)的字符的位置必须连续,后者(子序列LCS)则不必。比如字符串acdfg同akdfc的最长公共子串为df,而他们的最长公共子序列是adf。LCS可以使用动态规划法解决。
- Ziv-Lampel无损压缩算法。 LZW算法的基本原理是利用编码数据本身存在字符串重复特性来实现数据压缩,所以一个很好的选择是使用后缀树的形式来组织存储字符串及其对应压缩码值的字典。
- 找出字符串S的最长回文子串S1。例如:XMADAMYX的最长回文子串是MADAM(此即为上面所说的第二个问题:最长回文问题,本文第二部分将详细阐述此问题)。
- 多模式串的模式匹配问题(suffix_array + 二分)。
本文第一部分,咱们就来了解这个Trie树,然后自然而然过渡到第二部分、后缀树,接着进入第三部分、详细阐述后缀树的构造方法-Ukkonen,最后第四部分、对自动机,KMP算法,Extend-KMP,后缀树,后缀数组,trie树,trie图及其应用做个全文概括性总结。权作此番阐述,以备不时之需,在需要的时候便可手到擒来。ok,有任何问题,欢迎不吝指正或赐教。谢谢。
第一部分、Trie树
1.1、什么是Trie树
Trie树,即字典树,又称单词查找树或键树,是一种树形结构,是一种哈希树的变种。典型应用是用于统计和排序大量的字符串(但不仅限于字符串),所以经常被搜索引擎系统用于文本词频统计。它的优点是:最大限度地减少无谓的字符串比较,查询效率比哈希表高。
Trie的核心思想是空间换时间。利用字符串的公共前缀来降低查询时间的开销以达到提高效率的目的。
它有3个基本性质:
- 根节点不包含字符,除根节点外每一个节点都只包含一个字符。
- 从根节点到某一节点,路径上经过的字符连接起来,为该节点对应的字符串。
- 每个节点的所有子节点包含的字符都不相同。
1.2、树的构建
分析:这题当然可以用hash来解决,但是本文重点介绍的是trie树,因为在某些方面它的用途更大。比如说对于某一个单词,我们要询问它的前缀是否出现过。这样hash就不好搞了,而用trie还是很简单。
现在回到例子中,如果我们用最傻的方法,对于每一个单词,我们都要去查找它前面的单词中是否有它。那么这个算法的复杂度就是O(n^2)。显然对于100000的范围难以接受。现在我们换个思路想。假设我要查询的单词是abcd,那么在他前面的单词中,以b,c,d,f之类开头的我显然不必考虑。而只要找以a开头的中是否存在abcd就可以了。同样的,在以a开头中的单词中,我们只要考虑以b作为第二个字母的,一次次缩小范围和提高针对性,这样一个树的模型就渐渐清晰了。
好比假设有b,abc,abd,bcd,abcd,efg,hii 这6个单词,我们构建的树就是如下图这样的:
ok,如上图所示,对于每一个节点,从根遍历到他的过程就是一个单词,如果这个节点被标记为 红色,就表示这个单词存在,否则不存在。
那么,对于一个单词,我只要顺着他从根走到对应的节点,再看这个节点是否被标记为红色就可以知道它是否出现过了。把这个节点标记为红色,就相当于插入了这个单词。
这样一来我们查询和插入可以一起完成(重点体会这个查询和插入是如何一起完成的,稍后,下文具体解释),所用时间仅仅为单词长度,在这一个样例,便是10。
我们可以看到,trie树每一层的节点数是26^i级别的。所以为了节省空间。我们用动态链表,或者用数组来模拟动态。空间的花费,不会超过单词数×单词长度。
1.3、前缀查询
- 最容易想到的:即从字符串集中从头往后搜,看每个字符串是否为字符串集中某个字符串的前缀,复杂度为O(n^2)。
- 使用hash:我们用hash存下所有字符串的所有的前缀子串,建立存有子串hash的复杂度为O(n*len),而查询的复杂度为O(n)* O(1)= O(n)。
- 使用trie:因为当查询如字符串abc是否为某个字符串的前缀时,显然以b,c,d....等不是以a开头的字符串就不用查找了。所以建立trie的复杂度为O(n*len),而建立+查询在trie中是可以同时执行的,建立的过程也就可以成为查询的过程,hash就不能实现这个功能。所以总的复杂度为O(n*len),实际查询的复杂度也只是O(len)。(说白了,就是Trie树的平均高度h为len,所以Trie树的查询复杂度为O(h)=O(len)。好比一棵二叉平衡树的高度为logN,则其查询,插入的平均时间复杂度亦为O(logN))。
- 在hash中,例如现在要输入两个串911,911456,如果要同时查询这两个串,且查询串的同时若hash中没有则存入。那么,这个查询与建立的过程就是先查询其中一个串911,没有,然后存入9、91、911;而后查询第二个串911456,没有然后存入9、91、911、9114、91145、911456。因为程序没有记忆功能,所以并不知道911在输入数据中出现过,只是照常以例行事,存入9、91、911、9114、911...。也就是说用hash必须先存入所有子串,然后for循环查询。
- 而trie树中,存入911后,已经记录911为出现的字符串,在存入911456的过程中就能发现而输出答案;倒过来亦可以,先存入911456,在存入911时,当指针指向最后一个1时,程序会发现这个1已经存在,说明911必定是某个字符串的前缀。
1.4、查询
可以看出: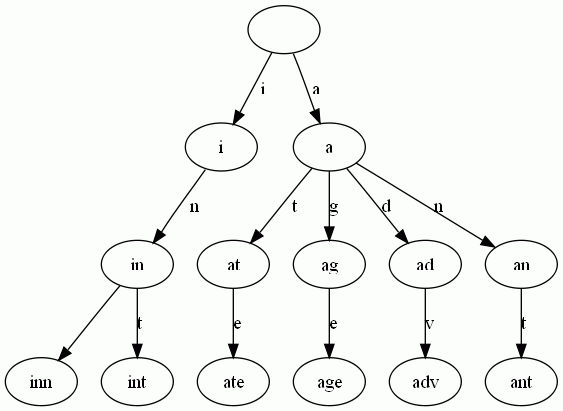
- 每条边对应一个字母。
- 每个节点对应一项前缀。叶节点对应最长前缀,即单词本身。
- 单词inn与单词int有共同的前缀“in”, 因此他们共享左边的一条分支,root->i->in。同理,ate, age, adv, 和ant共享前缀"a",所以他们共享从根节点到节点"a"的边。
搭建Trie的基本算法也很简单,无非是逐一把每则单词的每个字母插入Trie。插入前先看前缀是否存在。如果存在,就共享,否则创建对应的节点和边。比如要插入单词add,就有下面几步:
- 考察前缀"a",发现边a已经存在。于是顺着边a走到节点a。
- 考察剩下的字符串"dd"的前缀"d",发现从节点a出发,已经有边d存在。于是顺着边d走到节点ad
- 考察最后一个字符"d",这下从节点ad出发没有边d了,于是创建节点ad的子节点add,并把边ad->add标记为d。
1.5、Trie树的应用
- 3、有一个1G大小的一个文件,里面每一行是一个词,词的大小不超过16字节,内存限制大小是1M。返回频数最高的100个词。
- 9、1000万字符串,其中有些是重复的,需要把重复的全部去掉,保留没有重复的字符串。请怎么设计和实现?
- 10、 一个文本文件,大约有一万行,每行一个词,要求统计出其中最频繁出现的前10个词,请给出思想,给出时间复杂度分析。
- 13、寻找热门查询:
- 搜索引擎会通过日志文件把用户每次检索使用的所有检索串都记录下来,每个查询串的长度为1-255字节。假设目前有一千万个记录,这些查询串的重复读比较高,虽然总数是1千万,但是如果去除重复和,不超过3百万个。一个查询串的重复度越高,说明查询它的用户越多,也就越热门。请你统计最热门的10个查询串,要求使用的内存不能超过1G。
(1) 请描述你解决这个问题的思路;
(2) 请给出主要的处理流程,算法,以及算法的复杂度。
第二部分、后缀树
2.1、后缀树的定义
后缀树(Suffix tree)是一种数据结构,能快速解决很多关于字符串的问题。后缀树的概念最早由Weiner 于1973年提出,既而由McCreight 在1976年和Ukkonen在1992年和1995年加以改进完善。
后缀,顾名思义,甚至通俗点来说,就是所谓后缀就是后面尾巴的意思。比如说给定一长度为n的字符串S=S1S2..Si..Sn,和整数i,1 <= i <= n,子串SiSi+1...Sn便都是字符串S的后缀。
以字符串S=XMADAMYX为例,它的长度为8,所以S[1..8], S[2..8], ... , S[8..8]都算S的后缀,我们一般还把空字串也算成后缀。这样,我们一共有如下后缀。对于后缀S[i..n],我们说这项后缀起始于i。
S[1..8], XMADAMYX, 也就是字符串本身,起始位置为1
S[2..8], MADAMYX,起始位置为2
S[3..8], ADAMYX,起始位置为3
S[4..8], DAMYX,起始位置为4
S[5..8], AMYX,起始位置为5
S[6..8], MYX,起始位置为6
S[7..8], YX,起始位置为7
S[8..8], X,起始位置为8
空字串,记为$。
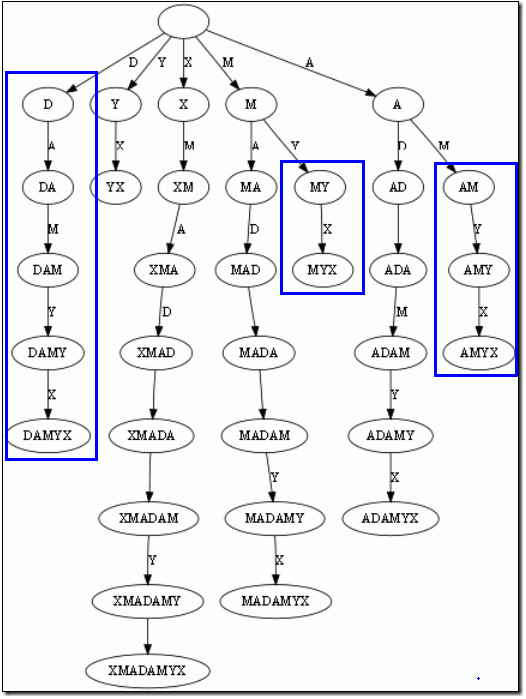
而后缀树,就是包含一则字符串所有后缀的压缩Trie。把上面的后缀加入Trie后,我们得到下面的结构:
仔细观察上图,我们可以看到不少值得压缩的地方。比如蓝框标注的分支都是独苗,没有必要用单独的节点同边表示。如果我们允许任意一条边里包含多个字 母,就可以把这种没有分叉的路径压缩到一条边。另外每条边已经包含了足够的后缀信息,我们就不用再给节点标注字符串信息了。我们只需要 在叶节点上标注上每项后缀的起始位置。于是我们得到下图:
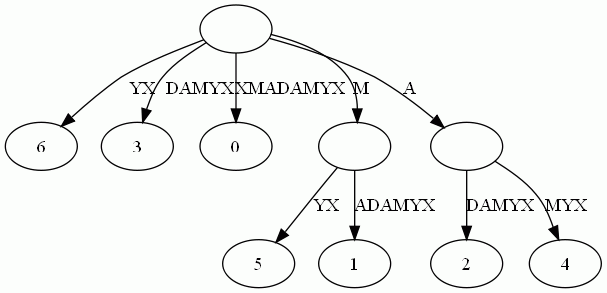
这样的结构丢失了某些后缀。比如后缀X在上图中消失了,因为它正好是字符串XMADAMYX的前缀。为了避免这种情况,我们也规定每项后缀不能是其它后缀的前缀。要解决这个问题其实挺简单,在待处理的子串后加一个空字串就行了。例如我们处理XMADAMYX前,先把XMADAMYX变为 XMADAMYX$,于是就得到suffix tree--后缀树了,如下图所示:
2.2、后缀树与回文问题的关联
那后缀树同最长回文有什么关系呢?我们得先知道两个简单概念:
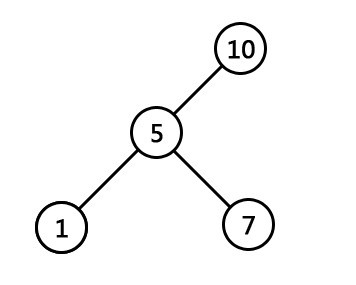
- 最低共有祖先,LCA(Lowest Common Ancestor),也就是任意两节点(多个也行)最长的共有前缀。比如下图中,节点7同节点1的共同祖先是节点5与节点10,但最低共同祖先是5。 查找LCA的算法是O(1)的复杂度,当然,代价是需要对后缀树做复杂度为O(n)的预处理。
- 广义后缀树(Generalized Suffix Tree)。传统的后缀树处理一坨单词的所有后缀。广义后缀树存储任意多个单词的所有后缀。例如下图是单词XMADAMYX与XYMADAMX的广义后缀 树。注意我们需要区分不同单词的后缀,所以叶节点用不同的特殊符号与后缀位置配对。
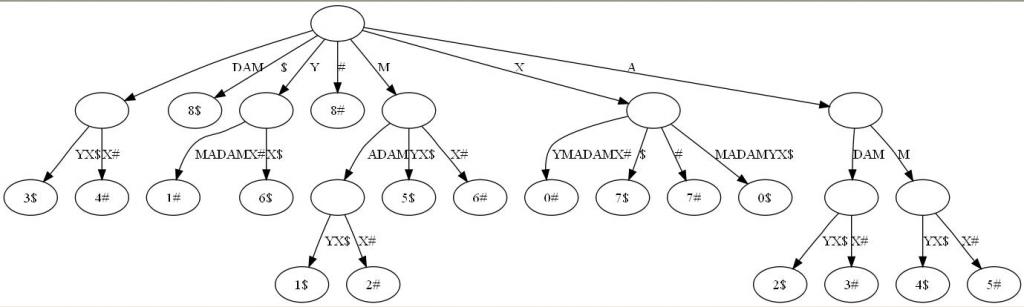
2.3、最长回文问题的解决
有了上面的概念,本文引言中提出的查找最长回文问题就相对简单了。咱们来回顾下引言中提出的回文问题的具体描述:找出给定字符串里的最长回文。例如输入XMADAMYX,则输出MADAM。思维的突破点在于考察回文的半径,而不是回文本身。所谓半径,就是回文对折后的字串。比如回文MADAM 的半径为MAD,半径长度为3,半径的中心是字母D。显然,最长回文必有最长半径,且两条半径相等。还是以MADAM为例,以D为中心往左,我们得到半径 DAM;以D为中心向右,我们得到半径DAM。二者肯定相等。因为MADAM已经是单词XMADAMYX里的最长回文,我们可以肯定从D往左数的字串 DAMX与从D往右数的子串DAMYX共享最长前缀DAM。而这,正是解决回文问题的关键。现在我们有后缀树,怎么把从D向左数的字串DAMX变成后缀 呢?
到这个地步,答案应该明显:把单词XMADAMYX翻转(XMADAMYX=>XYMADAMX,DAMX就变成后缀了)就行了。于是我们把寻找回文的问题转换成了寻找两坨后缀的LCA的问题。当然,我们还需要知道 到底查询那些后缀间的LCA。很简单,给定字符串S,如果最长回文的中心在i,那从位置i向右数的后缀刚好是S(i),而向左数的字符串刚好是翻转S后得到的字符串S‘的后缀S'(n-i+1)。这里的n是字符串S的长度。
可能上面的阐述还不够直观,我再细细说明下:
1、首先,还记得本第二部分开头关于后缀树的定义么: “先说说后缀的定义,顾名思义,甚至通俗点来说,就是所谓后缀就是后面尾巴的意思。比如说给定一长度为n的字符串S=S1S2..Si..Sn,和整数i,1 <= i <= n,子串SiSi+1...Sn便都是字符串S的后缀。”
以字符串S=XMADAMYX为例,它的长度为8,所以S[1..8], S[2..8], ... , S[8..8]都算S的后缀,我们一般还把空字串也算成后缀。这样,我们一共有如下后缀。对于后缀S[i..n],我们说这项后缀起始于i。
S[1..8], XMADAMYX, 也就是字符串本身,起始位置为1
S[2..8], MADAMYX,起始位置为2
S[3..8], ADAMYX,起始位置为3
S[4..8], DAMYX,起始位置为4
S[5..8], AMYX,起始位置为5
S[6..8], MYX,起始位置为6
S[7..8], YX,起始位置为7
S[8..8], X,起始位置为8
空字串,记为$。
2、对单词XMADAMYX而言,回文中心为D,那么D向右的后缀DAMYX假设是S(i)(当N=8,i从1开始计数,i=4时,便是S(4..8));而对于翻转后的单词XYMADAMX而言,回文中心D向右对应的后缀为DAMX,也就是S'(N-i+1)((N=8,i=4,便是S‘(5..8)) 。此刻已经可以得出,它们共享最长前缀,即LCA(DAMYX,DAMX)=DAM。有了这套直观解释,算法自然呼之欲出:
- 预处理后缀树,使得查询LCA的复杂度为O(1)。这步的开销是O(N),N是单词S的长度 ;
- 对单词的每一位置i(也就是从0到N-1),获取LCA(S(i), S‘(N-i+1)) 以及LCA(S(i+1), S’(n-i+1))。查找两次的原因是我们需要考虑奇数回文和偶数回文的情况。这步要考察每坨i,所以复杂度是O(N) ;
- 找到最大的LCA,我们也就得到了回文的中心i以及回文的半径长度,自然也就得到了最长回文。总的复杂度O(n)。
上面大致描述了后缀树的基本思路。要想写出实用代码,至少还得知道下面的知识:
- 创建后缀树的O(n)算法。此算法有很多种,无论Peter Weiner的73年年度最佳算法,还是Edward McCreight1976的改进算法,还是1995年E. Ukkonen大幅简化的算法(本文第4部分将重点阐述这种方法),还是Juha Kärkkäinen 和 Peter Sanders2003年进一步简化的线性算法,都是O(n)的时间复杂度。至于实际中具体选择哪一种算法,可依实际情况而定。
- 实现后缀树用的数据结构。比如常用的子结点加兄弟节点列表,Directed 优化后缀树空间的办法。比如不存储子串,而存储读取子串必需的位置。以及Directed Acyclic Word Graph,常缩写为黑哥哥们挂在嘴边的DAWG。
2.4、后缀树的应用
后缀树的用途,总结起来大概有如下几种- 查找字符串o是否在字符串S中。
方案:用S构造后缀树,按在trie中搜索字串的方法搜索o即可。
原理:若o在S中,则o必然是S的某个后缀的前缀。
例如S: leconte,查找o: con是否在S中,则o(con)必然是S(leconte)的后缀之一conte的前缀.有了这个前提,采用trie搜索的方法就不难理解了。 - 指定字符串T在字符串S中的重复次数。
方案:用S+’$'构造后缀树,搜索T节点下的叶节点数目即为重复次数
原理:如果T在S中重复了两次,则S应有两个后缀以T为前缀,重复次数就自然统计出来了。 - 字符串S中的最长重复子串
方案:原理同2,具体做法就是找到最深的非叶节点。
这个深是指从root所经历过的字符个数,最深非叶节点所经历的字符串起来就是最长重复子串。
为什么要非叶节点呢?因为既然是要重复,当然叶节点个数要>=2。 - 两个字符串S1,S2的最长公共部分
方案:将S1#S2$作为字符串压入后缀树,找到最深的非叶节点,且该节点的叶节点既有#也有$(无#)。
后缀树的代码实现,下期再续。第二部分、后缀树完。
第三部分、后缀树的构造方法-Ukkonen
接下来,咱们来了解后缀树的构造方法-Ukkomen。为了兼顾上文内容,以及加深印象,本部分打算从Trie树从头到位重新开始阐述一切。
Ukkonen的构造法O(n), 它比Sartaj Sahni的构造法O(nr), r为字母表大小 在时间上更有优势. 但我们不能说Sartaj Sahni的算法慢, 因为r往往会很小, 因此实际效率也接近线性, 两种构造法在思想上均有可取之处.
3.1、问题的起源
字符串匹配问题是程序员经常要面对的问题. 字符串匹配算法的改进可以使许多工程受益良多, 比如数据压缩和DNA排列。你可以把自己想象成一名工作于DNA排列工程的程序员. 那些基因研究者们天天忙着分切病毒的基因材料, 制造出一段一段的核苷酸序列. 他们把这些序列发到你的服务器里, 指望你在基因数据库中定位. 要知道, 你的数据库里有数百种病毒的数据, 而一个特定的病毒可以有成千上万的碱基. 你的程序必须像C/S工程那样实时向博士们反馈信息, 这需要一个很好的方案。
很明显, 在这个问题上采取暴力算法是极其低效的. 这种方法需要你在基因数据库里对比每一个核苷酸, 测试一个较长的基因段基本会把你的C/S系统变成一台古老的批处理机。
3.2、直觉上的解决方法
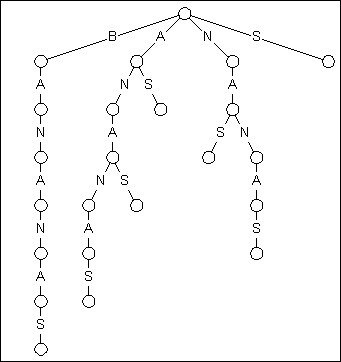
由于基因数据库一般是不变的, 通过预处理来把搜索简化或许是个好主意. 一种预处理的方法是建立一棵Trie. 我们通过Trie引申出一种东西叫作后缀Trie. (后缀Trie离后缀树仅一步之遥.) 首先, Trie是一种n叉树, n为字母表大小, 每个节点表示从根节点到此节点所经过的所有字符组成的字符串. 而后缀Trie的 “后缀” 说明这棵Trie包含了所给字段的所有后缀 (也许正是一个病毒基因).
图1 BANANAS的后缀Trie
上展示了文本BANANAS的后缀Trie. 关于这棵Trie有两个地方需要注意. 第一, 从根节点开始, BANANAS的每一个后缀都插入到Trie中, 包括BANANAS, ANANAS, NANAS, ANAS, NAS, AS, S. 第二, 鉴于这种结构, 你可以通过从根节点往下匹配的方式搜索到单词的任何一个子串.
这里所说的第二点正是我们认为后缀Trie优秀的原因. 如果你输入一个长度为N的文本并想在其中搜索一个长度为M的串, 传统的暴力匹配需要进行N*M次字符对比, 而一些改进过的匹配技术, 比如像Boyer-Moore算法, 可以在O(N+M)的时间开销内解决问题, 平均效率更是令人满意. 然而, 后缀Trie亮出了O(M)的牌子, 彻底鄙视了其他算法的成绩, 后缀Trie对比的次数仅仅相当于被搜索串的长度!
这确实是可圈可点的威力, 这意味着你能通过仅仅7次对比便在莎士比亚所有作品中找出BANANAS. 但有一点我们可不能忘了, 构造后缀Trie也是需要时间的.
后缀Trie之所以没有家喻户晓正是因为构造它需要O(n2)的时间和空间. 平方级的开销使它在最需要它的领域 --- 长串搜索 中被拒之门外.
3.3、横空出世
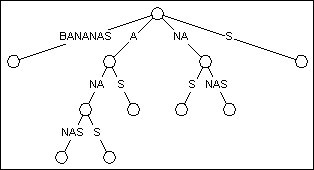
直到1976年, Edward McCreigh发表了一篇论文, 咱们的后缀树问世了. 后缀Trie的困境被彻底打破.
后缀树跟后缀Trie有着一样的布局, 但它把只有一个儿子的节点给剔除了. 这个过程被称为路径压缩, 这意味着树上的某些边将表示一个序列而不是单独的字符.
图2 BANANAS的后缀树
图2是由图1的后缀Trie转化而来的后缀树. 你会发现这树基本还是那个形状, 只是节点变少了. 在剔除了只有一个儿子的节点之后, 总节点数由23降为11. 经过证明, 在最坏情况下, 后缀树的节点数也不会超过2N (N为文本的长度). 这使构造后缀树的线性时空开销成为可能.
然而, McCreight最初的构造法是有些缺陷的, 原则上它要按逆序构造, 也就是说字符要从末端开始插入. 如此一来, 便不能作为在线算法, 它变得更加难以应用于实际问题, 如数据压缩.
20年后, 来自赫尔辛基理工大学的Esko Ukkonen把原算法作了一些改动, 把它变成了从左往右. 本文接下来的所有描述和代码都是基于Esko Ukkonen的成果.
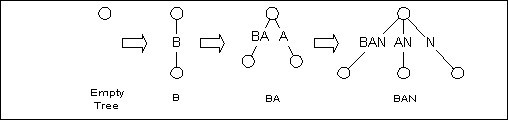
对于所给的文本T, Esko Ukkonen的算法是由一棵空树开始, 逐步构造T的每个前缀的后缀树. 比如我们构造BANANAS的后缀树, 先由B开始, 接着是BA, 然后BAN, … . 不断更新直到构造出BANANAS的后缀树.
图3 逐步构造后缀树
3.4、初窥门径
加入一个新的前缀需要访问树中已有的后缀. 我们从最长的一个后缀开始(图3中的BAN), 一直访问到最短的后缀(空后缀). 每个后缀会在以下三种节点的其中一种结束.
- 一个叶节点. 这个是常识了, 图4中标号为1, 2, 4, 5的就是叶节点.
- 一个显式节点. 图4中标号为0, 3的是显式节点, 它表示该节点之后至少有两条边.
- 一个隐式节点. 图4中, 前缀BO, BOO, 或者非前缀OO, 它们都在某条表示序列的边上结束, 这些位置就叫作隐式节点. 它表示后缀Trie中存在的由于路径压缩而剔除的节点. 在后缀树的构造过程中, 有时要把一些隐式节点转化为显式节点。
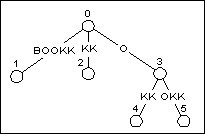
图4 加入BOOK之后的BOOKKEEPER
(也就是BOOK的后缀树)
如图4, 在加入BOOK之后, 树中有5个后缀(包括空后缀). 那么要构造下一个前缀BOOKK的后缀树的话, 只需要访问树中已存在的每一个后缀, 然后在它们的末尾加上K.
前4个后缀BOOK, OOK, OK和K都在叶节点上结束. 由于我们要路径压缩, 只需要在通往叶节点的边上直接加一个字符, 而不需要创建一个新节点.
在所有叶节点更新之后, 我们还需要在空后缀后面加上K. 这时候我们发现已经存在一条从0节点出发的边的首字符为K, 没必要画蛇添足了. 换句话说, 新加入的后缀K可以在0节点和2节点之间的隐式节点中找到. 最终形态见图5.
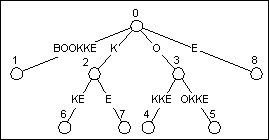
图5 加入BOOKK之后的BOOKKEEPER
相比图4, 树的结构没有发生变化
如果你是一位敏感的读者, 可能要发问了, 如果加入K我们什么都不做的话, 在查找的时候如何知道它到底是一个后缀呢还是某个后缀的一截? 如果你同时又是一位熟悉字符串算法的朋友, 心里可能马上就有答案了 --- 我们只需要在文本后面加个字母表以外的字符, 比如$或者#. 那我们查找到K$或K#的话就说明这是一个后缀了.
3.5、稍微麻烦一点的事情
从图4到图5这个更新过程是相对简单的, 其中我们执行了两种更新: 一种是将某条边延长, 另一种是啥都不做. 但接下来往图5继续加入BOOKKE, 我们则会遇到另外两种更新:
- 创建一个新节点来割开某一隐式节点所处的边, 并在其后加一条新边.
- 在显式节点后加一条新边.
图6先分割, 再添加
当我们往图5的树中加入BOOKKE的时候, 我们是从已存在的最长后缀BOOKK开始, 一直操作到最短的后缀空后缀. 更新最长的后缀必然是更新叶节点, 之前提到了, 非常简单. 除此之外, 图5中结束在叶节点上的后缀还有OOKK, OKK, KK. 图6的第一棵树展示了这一类节点的更新.
图5中首个不是结束在叶节点上的后缀是K. 这里我们先引入一个定义:
在每次更新后缀树的过程中, 第一个非叶节点称为激活节点. 它有以下性质:
- 所有比激活节点长的后缀都在叶节点上结束.
- 所有在激活节点之后加入的后缀都不在叶节点上结束.
后缀K在边KKE上的隐式节点结束. 在后缀树中我们要判断一个节点是不是非叶节点需要看它是否有跟待加入字符相同的儿子, 即本例中的E.
一眼可以看出, KKE中的第一个K只有一个儿子: K. 所以它是非叶节点(这里同时也是激活节点), 我们要给他加一个儿子来表示E. 这个过程有两个步骤:
- 在第一个K和第二个K之间把边分割开, 于是第一个K(隐式节点)成了一个显式节点, 如图6第二棵树.
- 在刚刚变身而来的显式节点后加一个新节点表示E, 如图6第三棵树. 由此我们又多了一个叶节点。
后缀K更新之后, 别忘了还有空后缀. 空后缀在根节点(节点0)结束, 显然此时根节点是一个显式节点. 我们看一下它后面有没有以E开头的边---没有, 那么加入一个新的叶节点(如果存在以E开头的边, 则不用任何操作). 最终如图7.
图7
3.6、归纳, 反思, 优化
借助后缀树的特性, 我们可以做出一个相当有效的算法. 首先一个重要的特性是: 一朝为叶, 终生为叶. 一个叶节点自诞生以后绝不会有子孙. 更重要的是, 每当我们往树上加入一个新的前缀, 每一条通往叶节点的边都会延长一个字符(新前缀的最后一个字符). 这使得处理通往叶节点的边变得异常简单, 我们完全可以在创建叶节点的时候就把当前字符到文本末的所有字符一股脑塞进去. 是的, 我们不需要知道后面的字符是啥, 但我们知道它们最终都要被加进去. 因此, 一个叶节点诞生的时候, 也正是它可以被我们遗忘的时候. 你可能会担心通往叶节点的边被分割了怎么办, 那也不要紧, 分割之后只是起点变了, 尾部该怎么着还是怎么着.
如此一来, 我们只需要关心显式节点和隐式节点上的更新.
还要提到一个节约时间的方法. 当我们遍历所有后缀时, 如果某个后缀的某个儿子跟待加字符(新前缀最后一个字符)相同, 那么我们当前前缀的所有更新就可以停止了. 如果你理解了后缀树的本质, 你会知道一旦待加字符跟某个后缀的某个儿子相同, 那么更短的后缀必然也有这个儿子. 我们不妨把首个这样的节点定义为结束节点. 比结束节点长的后缀必然是叶节点, 这一点很好解释, 要么本来就是叶节点, 要么就是新创建的节点(新创建的必然是叶节点). 这意味着, 每一个前缀更新完之后, 当前的结束节点将成为下一轮更新的激活节点.
好了, 现在我们可以把后缀树的更新限制在激活节点和结束节点之间, 效率有了很大的改善. 整理成伪代码如下:
Update( 新前缀 )
{
当前后缀 = 激活节点
待加字符 = 新前缀最后一个字符
done = false;
while ( !done ) {
if ( 当前后缀在显式节点结束 )
{
if ( 当前节点后没有以待加字符开始的边 )
在当前节点后创建一个新的叶节点
else
done = true;
} else {
if ( 当前隐式节点的下一个字符不是待加字符 )
{
从隐式节点后分割此边
在分割处创建一个新的叶节点
} else
done = true;
if ( 当前后缀是空后缀 )
done = true;
else
当前后缀 = 下一个更短的后缀
}
激活节点 = 当前后缀
}
3.7、后缀指针
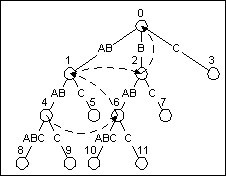
上面的伪代码看上去很完美, 但它掩盖了一个问题. 注意到第21行, “下一个更短的后缀”, 如果呆板地沿着树枝去搜索我们想要的后缀, 那这种算法就不是线性的了. 要解决此问题, 我们得附加一种指针: 后缀指针. 后缀指针存在于每个结束在非叶节点的后缀上, 它指向“下一个更短的后缀”. 即, 如果一个后缀表示文本的第0到第N个字符, 那么它的后缀指针指向的节点表示文本的第1到第N个字符.
图8是文本ABABABC的后缀树. 第一个后缀指针在表示ABAB的节点上. ABAB的后缀指针指向表示BAB的节点. 同样地, BAB也有它的后缀指针, 指向AB. 如此这般.
图8 加上后缀指针(虚线)的ABABABC的后缀树
介绍一下如何创建后缀指针. 后缀指针的创建是跟后缀树的更新同步的. 随着我们从激活节点移动到结束节点, 我把每个新的叶节点的父亲的路径保存下来. 每当创建一条新边, 我同时也在上一个叶节点的父亲那儿创建一个后缀指针来指向当前新边开始的节点. (显然, 我们不能在第一条新边上做这样的操作, 但除此之外都可以这么做.)
有了后缀指针, 就可以方便地一个后缀跳到另一个后缀. 这个关键性的附加品使得算法的时间上限成功降为O(N)。
第四部分、全文总结
自动机,KMP算法,Extend-KMP,后缀树,后缀数组,trie树,trie图及其应用
涉及到字符串的问题,无外乎这样一些算法和数据结构:自动机,KMP算法,Extend-KMP,后缀树,后缀数组,trie树,trie图及其应用。当然这些都是比较高级的数据结构和算法,而这里面最常用和最熟悉的大概是kmp,即使如此还是有相当一部分人也不理解kmp,更别说其他的了。当然一般的字符串问题中,我们只要用简单的暴力算法就可以解决了,然后如果暴力效率太低,就用个hash。当然hash也是一个面试中经常被用到的方法。这样看来,这样的一些算法和数据结构实际上很少会被问到,不过如果使用它们一般可以得到很好的线性复杂度的算法。
老实说,字符串问题的确挺复杂的,出来一个如果用暴力,hash搞不定,就很难再想其他的方法,当然有些可以用动态规划。下图主要说明下这些算法数据结构之间的关系。图中黄色部分主要写明了这些算法和数据结构的一些关键点。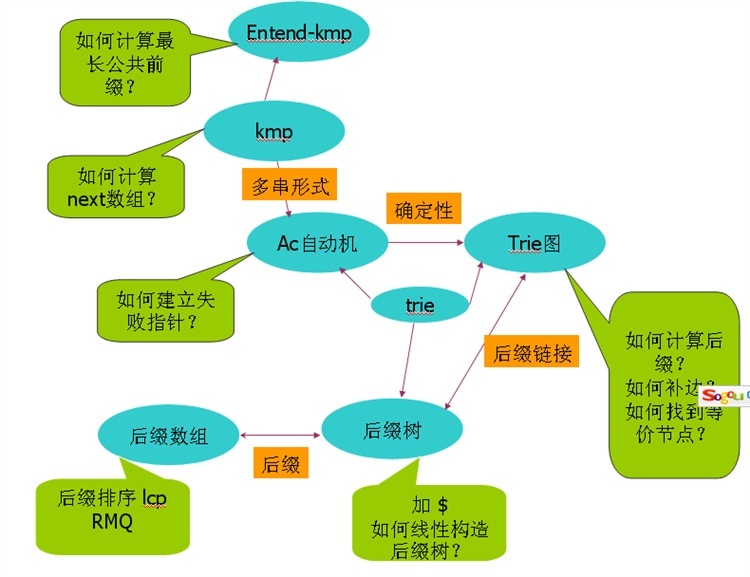
图中可以看到这样一些关系:extend-kmp 是kmp的扩展;ac自动机是kmp的多串形式;它是一个有限自动机;而trie图实际上是一个确定性有限自动机;ac自动机,trie图,后缀树实际上都是一种trie;后缀数组和后缀树都是与字符串的后缀集合有关的数据结构;trie图中的后缀指针和后缀树中的后缀链接这两个概念及其一致。
后缀树的构造可以用Ukkonen算法在线性时间内完成[,但是不仅构造算法实现相当复杂,而且后缀树存在着致命弱点:空间开销大且对大字母表时间效率不理想。至于后缀数组下次阐述,这里简单介绍下extend-kmp。而在介绍extend-kmp之前,咱们先要回顾下KMP算法。
kmp
首先这个匹配算法,主要思想就是要充分利用上一次的匹配结果,找到匹配失败时,模式串可以向前移动的最大距离。这个最大距离,必须要保证不会错过可能的匹配位置,因此这个最大距离实际上就是模式串当前匹配位置的next数组值。也就是max{Aj 是 Pi 的后缀 j < i},pi表示字符串A[1...i],Aj表示A[1...j]。模式串的next数组计算则是一个自匹配的过程。也是利用已有值next[1...i-1]计算next[i]的过程。我们可以看到,如果A[i] = A[next[i-1]+1] 那么next[i] = next[i-1],否则,就可以将模式串继续前移了。整个过程是这样的:
void next_comp(char * str){
int next[N+1];
int k = 0;
next[1] = 0;
//循环不变性,每次循环的开始,k = next[i-1]
for(int i = 2 ; i <= N ; i++){
//如果当前位置不匹配,或者还推进到字符串开始,则继续推进
while(A[k+1] != A[i] && k != 0){
k = next[k];
}
if(A[k+1] == A[i]) k++;
next[i] = k;
}
}
复杂度分析:从上面的过程可以看出,内部循环再不断的执行k = next[k],而这个值必然是在缩小,也就是是没执行一次k至少减少1;另一方面k的初值是0,而最多++ N次,而k始终保持非负,很明显减少的不可能大于增加的那些,所以整个过程的复杂度是O(N)。
上面是next数组的计算过程,而整个kmp的匹配过程与此类似。
extend-kmp
为什么叫做扩展-kmp呢,首先我们看它计算的内容,它是要求出字符串B的后缀与字符串A的最长公共前缀。extend[i]表示B[i...B_len] 与A的最长公共前缀长度,也就是要计算这个数组。观察这个数组可以知道,kmp可以判断A是否是B的一个子串,并且找到第一个匹配位置?而对于extend[]数组来说,则可以利用它直接解决匹配问题,只要看extend[]数组元素是否有一个等于len_A即可。显然这个数组保存了更多更丰富的信息,即B的每个位置与A的匹配长度。计算这个数组extend也采用了于kmp类似的过程。首先也是需要计算字符串A与自身后缀的最长公共前缀长度。我们设为next[]数组。当然这里next数组的含义与kmp里的有所过程。但它的计算,也是利用了已经计算出来的next[1...i-1]来找到next[i]的大小,整体的思路是一样的。
具体是这样的:观察下图可以发现
- 如果len < i 也就是说,len的长度还未覆盖到Ai,这样我们只要从头开始比较A[i...n]与A的最长公共前缀即可,这种情况下很明显的,每比较一次,必然就会让i+next[i]-1增加一.
- 如果len >= i,就是我们在图中表达的情形,这时我们可以看到i这个位置现在等于i-k+1这个位置的元素,这样又分两种情况:
- 如果 L = next[i-k+1] >= len-i+1,也就是说L处在第二条虚线的位置,这样我们可以看到next[i]的大小,至少是len-i+1,然后我们再从此处开始比较后面的还能否匹配,显然如果多比较一次,也会让i+A[i]-1多增加1.
- 如果 L < len-i+1 也就是说L处在第一条虚线位置,我们知道A与Ak在这个位置匹配,但Ak与Ai-k+1在这个位置不匹配,显然A与与Ai-k+1在这个位置也不会匹配,故next[i]的值就是L。这样next[i]的值就被计算出来了,从上面的过程中我们可以看到,next[i]要么可以直接由k这个位置计算出来,要么需要在逐个比较,但是如果需要比较,则每次比较会让k+next[k]-1的最大值加1.而整个过程中这个值只增不减,而且它有一个很明显的上界k+next[k]-1 < 2*len_A,可见比较的次数要被限制到这个数值之内,因此总的复杂度将是O(N)的。
本文参考及推荐阅读
- 维基百科:Trie树,后缀树;
- 兔子的算法集中营:后缀树 http://www.cppblog.com/superKiki/archive/2010/10/29/131786.aspx;
- 银河里的星星:字符串 http://duanple.blog.163.com/blog/static/709717672009825004092/;
- 后缀树的构造方法-Ukkonen详解 3xian / 三鲜 in GDUT http://blog.163.com/lazy_p/blog/static/13510721620108139476816/
- E.M. McCreight. A space-economical suffix tree construction algorithm. Journal of the ACM, 23:262-272, 1976.
- E. Ukkonen. On-line construction of suffix trees. Algorithmica, 14(3):249-260, September 1995.
- Mark Nelson. Fast string searching with suffix trees. 1996.
- fsdev的专栏:实用算法实现-第8篇后缀树和后缀数组 [1简介]
- 深度探索c++对象模型 侯捷译 P152~168。
- 结构之法算法之道blog:第三章、寻找最小的k个数,海量数据处理面试题集锦与Bit-map详解;
- http://www.ibaiyang.org/2013/01/06/suffix-tree-introduction/。
- 从头到尾彻底理解KMP(2014年8月22日版):http://blog.csdn.net/v_july_v/article/details/7041827





 本文详细介绍了Trie树和后缀树的基本概念、核心特性和应用案例,着重讲解了后缀树的定义、构造方法及与回文问题的关联,还提供了Ukkonen算法的深入解析。文章最后整合了多种字符串处理算法和数据结构的关系,形成了对Trie树、后缀树、自动机、KMP算法、Extend-KMP等的全面总结。
本文详细介绍了Trie树和后缀树的基本概念、核心特性和应用案例,着重讲解了后缀树的定义、构造方法及与回文问题的关联,还提供了Ukkonen算法的深入解析。文章最后整合了多种字符串处理算法和数据结构的关系,形成了对Trie树、后缀树、自动机、KMP算法、Extend-KMP等的全面总结。





















 16万+
16万+












