前言
目前为止,之前学习的几个算法的模型P(y|x;θ),在给定x的情况下y的条件分布。比如逻辑回归算法中,基础模型P(y|x;θ)的演化为 h(x)=g(θTx),g 是sigmod函数。这类的算法都是直接的去学习p(y|x)或者学习如何将输入x映射到{0,1}这样的标签中,我们称这类算法为判别学习算法。
这篇文章要讲述的是另外一个算法,假设有一个分类问题,主要为了学习区分大象(y=1)和小狗(y=0),当然是根据给定的一些动物的featurs来判定类别。之前的回归算法可能就会通过梯度上升算法算出一条直线来区分这两个类别,然后对于新的animal只要输入这个回归算法中,就能判别是在直线的哪一边,从而判断是属于什么动物。而另外一种方法就是,在数据集中,挑选出大象的数据,以这个数据集为基础建立一个模型,描述大象应该有的features,同理对于小狗也可以建立一个模型,学习小狗的一些features。这样就有两个不一样的模型,当有新的animal输入时,我们可以分别让这个新输入和大象模型与小狗模型进行匹配,观察这个新输入的animal更像哪一个类型,从而确定类别 。
Generative Learning Algorithms
类似上面这种我们称作是生成学习算法,举个例子,假设y的值{0,1},0代表是小狗,1代表是大象,那么p(x|y=0)是对小狗的features的建模,p(x|y=1)是对大象的features的建模。可以看出生成学习算法一开始是对p(x|y)建模而不是对p(y|x)建模,这个是跟判别算法有差异的地方。对p(x|y)建模后就可以通过贝叶斯法则来求出p(y|x)
下面是求p(y|x)要用的贝叶斯的一般性公式:
利用这一公式我们分别写出一下P(y=1|x)和p(y=0|x)的求解公式以及变化:
可以得出的结论就是下面红线标记的公式,这也是对p(x)建模的模型。
最终目的是为了预测p(y|x)我们可以用下面定义公式来计算:
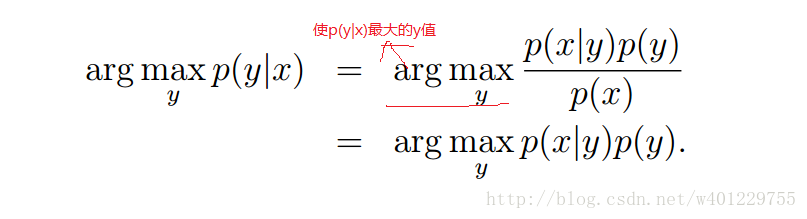
不用考虑分母p(x)的原因是: arg max的定义是求出使p(y|x)最大的y值,最后的结果是y值,而分母p(x)由上面的建模模型可以看出y值都是已经确定了0或1,所以p(x)是一个与y无关的数值,即常数。这个定义会在后面具体分析高斯模型的时候用到。
Gaussian discriminant analysis
第一个要研究的生成学习算法是GDA,在这个模型中我们假设p(x|y)是多元正态分布,接下来先讨论一下多元正态分布。
GDA也被称作是多元高斯分布,这是ng课件里面的定义,符号有点多直接截图了:
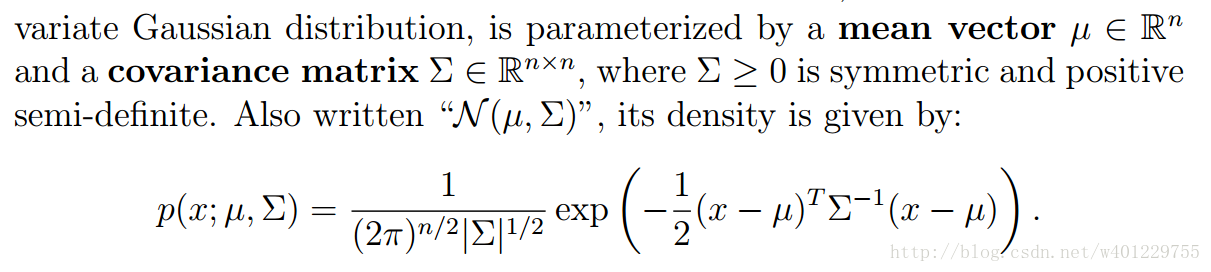
上面是由一般性的正态分布公式演化而来,简单介绍下其演化过程:
一一去对比公式中的各个式子都可以对上号,由于引进的是多元正态分布,也是多维高斯分布,所以用矩阵的方式来计算,式子中会有所变化。
当然,多维随机向量具有类似的概率规律时,称此随机向量遵从多维正态分布。多元正态分布有很好的性质,例如,多元正态分布的边缘分布仍为正态分布,它经任何线性变换得到的随机向量仍为多维正态分布,特别它的线性组合为一元正态分布。
下面是对多元高斯分布的均值公式:
期望值μ决定了其位置,其协方差∑决定了分布的幅度,具体的影响性,ng的视频及课件用了好几个形象化的例子来描述协方差的变化对分布形状的变化影响。这边就不做深入研究了。
GDA 模型是为了针对解决当输入的值是连续的随机值时,此时我们可以用GDA来建模,当然GDA也是生成学习算法类,所以也是对p(x|y)建模,下面研究一下GDA模型的建模过程,当然这个模型选的是多元正态分布:
下面是具体的模型公式:
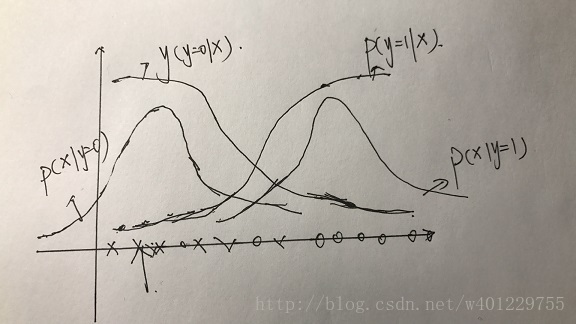
将这些模型用函数图形表现出来:
假设两个凸函数(对p(x|y的建模))形状的曲线就是正态分布的图像,中心位置不一样。其中我们预测p(y=1|x),明显在偏左边的区域p(y=0)的概率更大,所以p(y=1|x)的概率偏小,越往右,越靠近p(x|y=1)概率越大。同理p(y=0|x)也一样,最后发现预测出来的两条曲线跟逻辑回归的sigmod函数图形很相似,这里就不做详细描述了,课件和视频都有具体讲。
p(y)的建模公式其实就是伯努利模型,线面给出比较详细的公式以便理解:
对于上面的模型,一共涉及到了(∮,∑,u0,u1),这里虽然有两个不同的均值u0,u1,但是不影响使用同一个协方差∑,对于多参数的模型这边用log-likehood来估计:
接下来就是计算出各个参数取多少时,这个似然公式会取到最大值,课件直接给了以下结论:
具体代表的意义,图上有少许注释。其实自己学习到这里也是一头雾水,上面的几个式子琢磨了挺久没有思路,决定等以后顿悟之后再回头看这些到底是什么名堂。生成学习算法应该算是一类算法,高斯属于其中的一种,而且课件后面还介绍了逻辑回归和高斯判别的区别,总结来说就是我们以后使用逻辑回归的机会会比高斯判别更经常。所以高斯判别也就简单学习到这里了,后面有机会继续探索一下算法原型,争取代码实现出来。








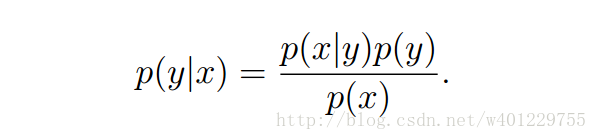

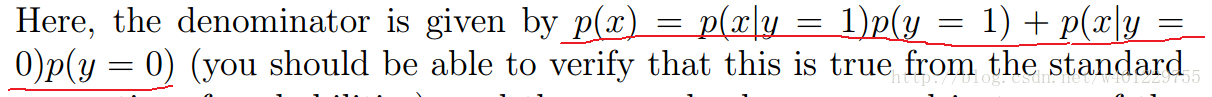

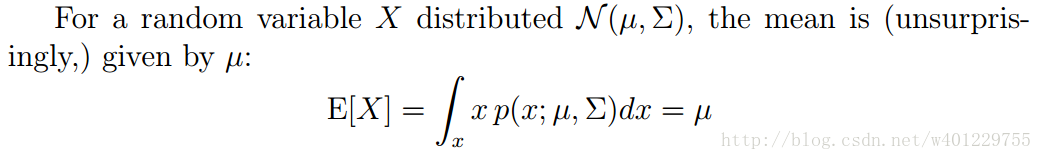
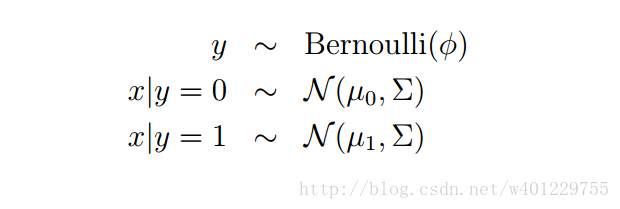
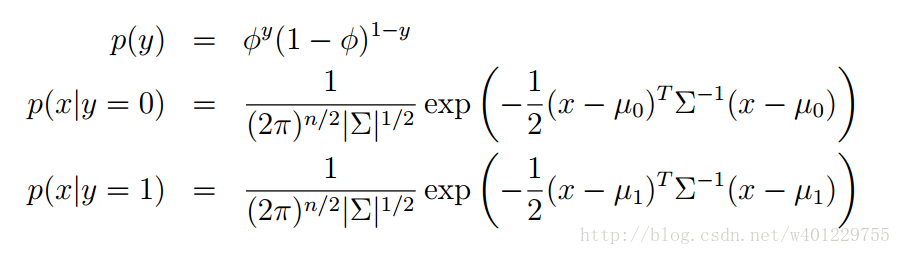
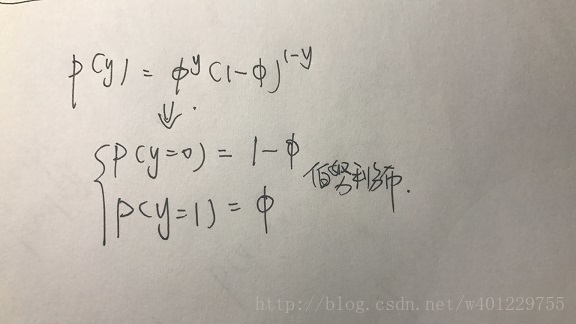
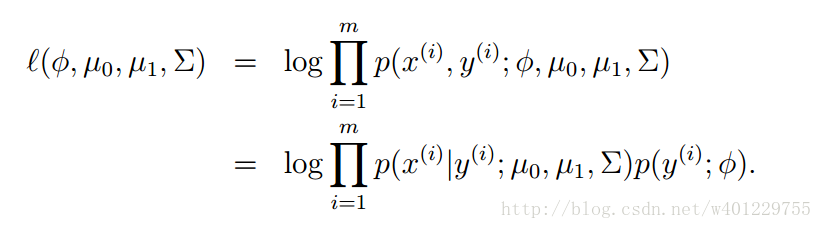














 2034
2034











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








