12.1 曲线拟合
12.1.1 曲线拟合的定义
曲线拟合(Curve Fitting)的数学定义是指用连续曲线近似地刻画或比拟平面上一组离散点所表示的坐标之间的函数关系,是一种用解析表达式逼近离散数据的方法。曲线拟合通俗的说法就是“拉曲线”,也就是将现有数据透过数学方法来代入一条数学方程式的表示方法。科学和工程遇到的很多问题,往往只能通过诸如采样、实验等方法获得若干离散的数据,根据这些数据,如果能够找到一个连续的函数(也就是曲线)或者更加密集的离散方程,使得实验数据与方程的曲线能够在最大程度上近似吻合,就可以根据曲线方程对数据进行数学计算,对实验结果进行理论分析,甚至对某些不具备测量条件的位置的结果进行估算。
12.1.2 简单线性数据拟合的例子
回想一下中学物理课的“速度与加速度”实验:假设某物体正在做加速运动,加速度未知,某实验人员从时间t0 = 3秒时刻开始,以1秒时间间隔对这个物体连续进行了12次测速,得到一组速度和时间的离散数据,请根据实验结果推算该物体的加速度。
| 时间 (秒) | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 速度(米/秒) | 8.41 | 9.94 | 11.58 | 13.02 | 14.33 | 15.92 | 17.54 | 19.22 |
| 时间 (秒) | 11 | 12 | 13 | 14 |
|
|
|
|
| 速度(米/秒) | 20.49 | 22.01 | 23.53 | 24.47 |
|
|
|
|
表 12 – 1 物体速度和时间的测量关系表
在选择了合适的坐标刻度之后,我们就可以在坐标纸上画出这些点。如图12–1所示,排除偏差明显偏大的测量值后,可以看出测量结果呈现典型的线性特征。沿着该线性特征画一条直线,使尽量多的测量点能够位于直线上,或与直线的偏差尽量小,这条直线就是我们根据测量结果拟合的速度与时间的函数关系。最后在坐标纸上测量出直线的斜率K,K就是被测物体的加速度,经过测量,我们实验测到的物体加速度值是1.48米/秒2。
图 12 – 1 实验法测量加速度的过程
12.2 最小二乘法曲线拟合
使用数学分析进行曲线拟合有很多常用的方法,这一节我们先介绍一下最简单的最小二乘法,并给出使用最小二乘法解决上一节给出的速度与加速度实验问题。
12.2.1 最小二乘法原理
最小二乘法(又称最小平方法)通过最小化误差的平方和寻找数据的最佳函数匹配,利用最小二乘法可以简便地求得未知的数据,并使得这些求得的数据与实际数据之间误差的平方和为最小,当然,做为一种插值方法使用时,最小二乘法也可以用于曲线拟合。使用最小二乘法进行曲线拟合是曲线拟合种早期的一种常用方法,不过,最小二乘法理论简单,计算量小,即便是在使用三次样条曲线或RBF(Radial Basis Function)进行曲线拟合大行其道的今天,最小二乘法在多项式曲线或直线的拟合问题上,仍然得到广泛地应用。使用最小二乘法,选取的匹配函数的模式非常重要,如果离散数据呈现的是指数变化规律,则应该选择指数形式的匹配函数模式,如果是多项式变化规律,则应该选择多项式匹配模式,如果选择的模式不对,拟合的效果就会很差,这也是使用最小二乘法进行曲线拟合时需要特别注意的一个地方。
下面以多项式模式为例,介绍一下使用最小二乘法进行曲线拟合的完整步骤。假设选择的拟合多项式模式是:
这m个等式相当于m个方程,a0,a1,…am是m个未知量,因此这m个方程组成的方程组是可解的,最小二乘法的第二步处理就是将其整理为针对a0,a1,…am的正规方程组。最终整理的方程组如下:
最小二乘法的第三步处理就是求解这个多元一次方程组,得到多项式的系数a0,a1,…am,,就可以得到曲线的拟合多项式函数。求解多元一次方程组的方法很多,高斯消元法是最常用的一种方法,下一节就简单介绍一下最小二乘算法实现所用的高斯消元法算法。
12.2.2 高斯消元法求解方程组
在数学上,高斯消元法是线性代数中的一个算法,可用来求解多元一次线性方程组,也可以用来求矩阵的秩,以及求可逆方阵的逆矩阵。高斯消元法虽然以数学家高斯的名字命名,但是最早出现在文献资料中应该是中国的《九章算术》。
高斯消元法的主要思想是通过对系数矩阵进行行变换,将方程组的系数矩阵由对称矩阵变为三角矩阵,从而达到消元的目的,最后通过回代逐个获得方程组的解。在消元的过程中,如果某一行的对角线元素的值太小,在计算过程中就会出现很大的数除以很小的数的情况,有除法溢出的可能,因此在消元的过程中,通常都会增加一个主元选择的步骤,通过行交换操作,将当前列绝对值最大的行交换到当前行位置,避免了除法溢出问题,增加了算法的稳定性。
高斯消元法算法实现简单,主要有两个步骤组成,第一个步骤就是通过选择主元,逐行消元,最终行程方程组系数矩阵的三角矩阵形式,第二个步骤就是逐步回代的过程,最终矩阵的对角线上的元素就是方程组的解。下面就给出高斯消元法的一个算法实现:
|
76 /*带列主元的高斯消去法解方程组,最后的解在matrixA的对角线上*/ 77 bool GuassEquation::Resolve(std::vector<double>& xValue) 78 { 79 assert(xValue.size() == m_DIM); 80 81 /*消元,得到上三角阵*/ 82 for(int i = 0; i < m_DIM - 1; i++) 83 { 84 /*按列选主元*/ 85 int pivotRow = SelectPivotalElement(i); 86 if(pivotRow != i)/*如果有必要,交换行*/ 87 { 88 SwapRow(i, pivotRow); 89 } 90 if(IsPrecisionZero(m_matrixA[i * m_DIM + i])) /*主元是0? 不存在唯一解*/ 91 { 92 return false; 93 } 94 /*对系数归一化处理,使行第一个系数是1.0*/ 95 SimplePivotalRow(i, i); 96 /*逐行进行消元*/ 97 for(int j = i + 1; j < m_DIM; j++) 98 { 99 RowElimination(i, j, i); 100 } 101 } 102 /*回代求解*/ 103 m_matrixA[(m_DIM - 1) * m_DIM + m_DIM - 1] = m_bVal[m_DIM - 1] /m_matrixA[(m_DIM - 1) * m_DIM + m_DIM - 1]; 104 for(int i = m_DIM - 2; i >= 0; i--) 105 { 106 double totalCof = 0.0; 107 for(int j = i + 1; j < m_DIM; j++) 108 { 109 totalCof += m_matrixA[i * m_DIM + j] * m_matrixA[j * m_DIM + j]; 110 } 111 m_matrixA[i * m_DIM + i] = (m_bVal[i] - totalCof) / m_matrixA[i * m_DIM+ i]; 112 } 113 114 /*将对角线元素的解逐个存入解向量*/ 115 for(int i = 0; i < m_DIM; i++) 116 { 117 xValue[i] = m_matrixA[i * m_DIM + i]; 118 } 119 120 return true; 121 } |
GuassEquation::Resolve()函数中m_matrixA是以一维数组形式存放的系数矩阵,m_DIM是矩阵的维数,SelectPivotalElement()函数从系数矩阵的第i列中选择绝对值最大的那个值所在的行,并返回行号,SwapRow()函数负责交换系数矩阵两个行的所有值,SimplePivotalRow()函数是归一化处理函数,通过除法操作将指定的行的对角线元素变换为1.0,以便简化随后的消元操作。
12.2.3 最小二乘法解决“速度与加速度”实验
根据12.2.1节对最小二乘法原理的分析,用程序实现最小二乘法曲线拟合的算法主要由两个步骤组成,第一个步骤就是根据给出的测量值生成关于拟合多项式系数的方程组,第二个步骤就是解这个方程组,求出拟合多项式的各个系数。根据对上文最终整理的正规方程组的分析,可以看出其系数有一定的关系,就是每一个方程式都比前一个方程式多乘了一个xi。因此,只需要完整计算出第一个方程式的系数,其他方程式的系数只是将前一个方程式的系数依次左移一位,然后单独计算出最后一个系数就可以了,此方法可以减少很多无谓的计算。求解多元一次方程组的方法就使用12.2.2节介绍的高斯消元法,其算法上一节已经给出。
这里给出一个最小二乘算法的完整实现,以12.1.2节的数据为例,因为数据结果明显呈现线性方程的特征,因此选择拟合多项式为v = v0 + at,v0和a就是要求解的拟合多项式系数。
|
99 bool LeastSquare(const std::vector<double>& x_value, const std::vector<double>&y_value, 100 int M, std::vector<double>& a_value) 101 { 102 assert(x_value.size() == y_value.size()); 103 assert(a_value.size() == M); 104 105 double *matrix = new double[M * M]; 106 double *b= new double[M]; 107 108 std::vector<double> x_m(x_value.size(), 1.0); 109 std::vector<double> y_i(y_value.size(), 0.0); 110 for(int i = 0; i < M; i++) 111 { 112 matrix[ARR_INDEX(0, i, M)] = std::accumulate(x_m.begin(), x_m.end(),0.0); 113 for(int j = 0; j < static_cast<int>(y_value.size()); j++) 114 { 115 y_i[j] = x_m[j] * y_value[j]; 116 } 117 b[i] = std::accumulate(y_i.begin(), y_i.end(), 0.0); 118 for(int k = 0; k < static_cast<int>(x_m.size()); k++) 119 { 120 x_m[k] *= x_value[k]; 121 } 122 } 123 for(int row = 1; row < M; row++) 124 { 125 for(int i = 0; i < M - 1; i++) 126 { 127 matrix[ARR_INDEX(row, i, M)] = matrix[ARR_INDEX(row - 1, i + 1, M)]; 128 } 129 matrix[ARR_INDEX(row, M - 1, M)] = std::accumulate(x_m.begin(),x_m.end(), 0.0); 130 for(int k = 0; k < static_cast<int>(x_m.size()); k++) 131 { 132 x_m[k] *= x_value[k]; 133 } 134 } 135 136 GuassEquation equation(M, matrix, b); 137 delete[] matrix; 138 delete[] b; 139 140 return equation.Resolve(a_value); 141 } |
将表12-1的数据带入算法,计算得到v0 = 4.05545455,a = 1.48818182,比作图法得到的结果更精确。以上算法是根据最小二乘法的理论推导系数方程,并求解系数方程得到拟合多项式的系数的一种实现方法,除此之外,还可以利用预先计算好的最小二乘解析理论直接求得拟合多项式的系数,读者可自行学习相关的实现算法。
12.3 三次样条曲线拟合
曲线拟合基本上就是一个插值计算的过程,除了最小二乘法,其他插值方法也可以被用于曲线拟合。常用的曲线拟合方法还有基于RBF(Radial Basis Function)的曲线拟合和三次样条曲线拟合。最小二乘法方法简单,便于实现,但是如果拟合模式选择不当,会产生较大的偏差,特别是对于复杂曲线的拟合,如果选错了模式,拟合的效果就很差。基于RBF(Radial Basis Function)的曲线拟合方法需要高深的数学基础,涉及多维空间理论,将低维的模式输入数据转换到高维空间中,使得低维空间内的线性不可分问题在高维空间内变得线性可分,这种数学分析方法非常强大,但是这种方法不宜得到拟合函数,因此在需要求解拟合函数的情况下使用起来不是很方便。
样条插值是一种工业设计中常用的、得到平滑曲线的一种插值方法,三次样条又是其中用的较为广泛的一种。使用三次样条曲线进行曲线拟合可以得到非常高精度的拟合结果,并且很容易得到拟合函数,本节的内容将重点介绍三次样条曲线拟合的原理和算法实现,并通过一个具体的例子将三次样条函数拟合的曲线与原始曲线对比显示,体会一下三次样条曲线拟合的惊人效果。
12.3.1 插值函数
前文提到过,曲线拟合的实质就是各种插值计算,因此,插值函数的选择决定了曲线拟合的效果。那么插值函数的数学定义是什么呢?若在[a, b]上给出n + 1个点a ≤ x0 < x1 < ⋯ < xn ≤ b,f(x) 是[a, b]上的实值函数, 要求一个具有n + 1个参量的函数s(x; a0,...,an) 使它满足
s(xi; a0,..., an) = f(xi) , i = 0, 1, ⋯, n (3.5)
则称s(x)为f(x) 在[a, b]上的插值函数. 若s(x) 关于参量a0, a1,...,an是线性关系, 即:
s(x) = a0s0(x) + a1s1(x) + ⋯ + ansn(x) (3.6)
s(x)就是多项式插值函数,如果si(x)是三角函数,则s(x)就是三角插值函数。
比较常用的多项式插值函数是牛顿插值多项式和拉格朗日插值多项式,但是在多项式的次数比较高的情况下,插值点数n过多会导致多项式插值在收敛性和稳定性上失去保证,因此,当插值点数n较大的情况下,一般不使用多项式插值,而采用样条插值或次数较低的最小二乘法插值。
12.3.2 样条函数的定义
在所有能够保证收敛性和稳定性的插值函数中,最常用的,也是最重要的插值函数就是样条插值函数。采用样条函数计算出的插值曲线和曲面在飞机、轮船和汽车等精密机械设计中都得到了广泛的应用。样条插值函数的数学定义是这样的:
设区间[a, b]上选取n - 1个节点(包括区间端点a和b共n + 1个节点),将其划分为n个子区间 a = x0 < x1 < ⋯ < xn = b, 如果存在函数s(x),使得s(x)满足以下两个条件:
(1) s(x) 在整个区间[a, b]上具有m - 1阶连续导数;
(2) s(x)在每个子区间[xi-1, xi], i= 1, 2, ⋯, n 上是m 次代数多项式(最高次数为m次);
则称s(x)是区间[a, b]上的m 次样条函数。假如区间[a, b]上存在实值函数f(x),使得每个节点处的值f(xi)与s(xi)相等,即
s(xi) = f(xi), i = 0, 1, …, n (3.7)
则称s(x)是实值函数f(x)的m 次样条插值函数。
当m = 1时,样条插值函数就是分段线性插值, 此时虽然s(x)是属于区间[a, b]上的函数, 但它不光滑(连一阶连续导数性质都不具备),不能满足工程设计要求。工程设计通常使用较多的是m = 3时的三次样条插值函数,此时样条函数具有二阶连续导数性质。
根据三次样条函数的定义,s(x)在每个子区间上的样条函数si(x)都是一个三次多项式,也就是说,三次样条函数s(x)由n个区间上的n个三次多项式组成,每个三次多项式可描述为以下形式:
si(x) = aix3 + bix2 + cix + di i = 1, 2, …, n (3.8)
因此,要确定完整的样条函数s(x)需要确定ai、bi、ci和di公4n个系数。根据样条函数的定义,s(x)在区间内的n - 1个节点处都是连续的,并且其一阶导数si‘(x)和二阶导数si“(x)都是连续的,根据连续函数的性质(xi的左右导数相等),我们可以得到3(n - 1)个条件:
si(xi - 0) = si+1(xi + 0) i = 1, 2, …, n-1
si‘(xi - 0) = si+1‘(xi + 0) i = 1, 2, …, n-1
si“(xi - 0) = si+1“(xi + 0) i = 1, 2, …, n-1 (3.9)
再加上插值函数在包括区间端点a(就是x0),b(就是xn)在内的n + 1个节点处满足s(xi) = f(xi),又可以得到n + 1个条件,这样就具备了4n – 2个条件。
12.3.3 边界条件
为了解决4n个系数组成的方程组,最终确定的s(x),需要再补充两个边界条件使之满足4n个条件。常用的边界条件有以下几种:
第一类边界条件,即满足s‘(x0) = f’(x0),s‘(xn) = f’(xn)两个条件,其中f(x)是实值函数。
第二类边界条件,即满足s”(x0) = f”(x0),s”(xn) = f”(xn)两个条件,其中f(x)是实值函数。特别情况下,当f”(x0) = f”(xn) = 0的时候,也就是s”(x0) = s”(xn) = 0的情况下,第二类边界条件又被称为自然边界条件。
当样条函数的实值函数f(x)是以[a, b]为周期的周期函数时,三次样条函数s(x)在两个端点处满足s‘(x0 - 0) = s‘(xn + 0)和s”(x0 - 0) = s”(xn + 0),这种情况又被成为第三类边界条件。
工程技术中常用的是第一类边界条件和第二类边界条件,以及第二类边界条件的特殊情况自然边界条件。理想情况下,也就是实值函数已知的情况下,可以通过实值函数直接计算出边界条件的值,否则的话,就只能通过测量和计算得到边界条件的值,有时候甚至只能给出经验估计值,工程技术中通常根据实际情况灵活使用各类边界条件。
12.3.4 推导三次样条函数
求三次样条插值函数s(x)的方法很多,其基本原理都是首先求出由待定系数组成的s(x),以及其一阶导数s’(x)和二阶导数s”(x),然后将其带入到12.3.2和12.3.3节列举的4n个条件中,得到关于待定系数的方程组,最后求解方程组得到待定系数,并最终确定插值函数s(x)。
求三次样条插值函数s(x)常用的方法是“三转角法”和“三弯矩法”。根据三次样条函数的性质,s(x)的一阶导数s’(x)是二次多项式, 二阶导数s”(x)是一次多项式(线性函数), “三转角法”和“三弯矩法”的主要区别是利用这两个特性推导插值函数s(x)、s’(x)和s”(x)的方式不同。“三转角法”利用s(x)的一阶导数s’(x)是二次多项式这个特性,对于子区间[xi, xi+1],利用抛物线插值公式获得一个通过xi和xi+1两个点的二次多项式做为s’(x),然后对s’(x)进行积分和微分(求导)运算,分别得到s(x),和s”(x),最后将它们带入4n个条件中求解系数方程组。“三弯矩法”则是利用s(x)的二阶导数s”(x)是一次多项式(线性函数)这个特性,对于子区间[xi, xi+1],首先假设一个通过xi和xi+1两个点的线性函数做为s”(x),然后对s”(x)进行连续两次积分运算得到s(x),再对s(x)进行求导得运算到s’(x),最后将它们带入4n个条件中求解系数方程组。这两种方法的本质是一样的,只是对s(x)的推导过程不同,接下来就介绍使用“三弯矩法”求解三次样条函数的方法。
三次样条函数的求解过程就是系数方程组的推导过程,使用“三弯矩法”推导系数方程组,首先要确定插值函数的二阶导数s”(x)。根据三次样条函数的性质,在每个子区间[xi, xi+1]上,其二阶导数s”(x)是个线性方程,现在假设在xi和xi+1两个端点的二阶导数值分别是Mi和Mi+1,也就是s”(xi) = Mi,s”(xi+1) = Mi+1,则经过xi和xi+1的两点式直线方程是:
从M0到Mn,有n+1个Mi的值需要求解,但是(3.20)只有n-1个等式,此时就需要用到两个边界条件了。
如果是使用第二类边界条件,则直接可以得到以下两个条件等式:
s”(x0) = M0 = f”(x0) = y0’ (3.21)
s”(xn) = Mn = f”(xn) = yn’ (3.22)
令d0 = 2y0’,dn = 2yn’,可以得到由第二类边界条件确定的两个方程:
2M0 = d0 (3.23)
2Mn = dn (3.24)
如果是使用第一类边界条件,即s‘(x0) = f’(x0),s‘(xn) = f’(xn)两个条件,则需要将这两个条件代入(3.16),通过计算得到两个条件等式。将s‘(x0) = y0’代入(3.16),得到:
将第二类边界条件得到的(3.23)和(3.24)或第一类边界条件得到的(3.27)和(3.28)与(3.20)中的n – 1个等式组合在一起就得到一个关于Mi的方程组,求解此方程组可以得到Mi的值,代入到(3.15)即可得到三次样条函数方程。以第一类边界条件得到的(3.27)和(3.28)为例,与(3.20)连立得到以下方程组:
这就是三弯矩方程组,其中Mi,i=0,1,…n就是三次样条函数s(x)的矩。根据(3.27)和(3.28),un = 1,v0 = 1,其余各系数可以通过(3.19)中的系数计算出来。这个方程组的系数矩阵是一个对角线矩阵,并且是一个严格对角占优的对角阵(ui和vi的值均小于主对角线的值,也就是ui和vi的值皆小于2),可以使用追赶法求解。下一节将介绍如何使用追赶法求解方程组,并给出求解的算法实现。
12.3.5 追赶法求解方程组
任意矩阵A,都可以通过克洛脱(Crout)分解得到两个三角矩阵:
其中y1=d1/l1,其余各项的递推计算关系是:
yi = (di – miyi-1)/li, i = 2,3,… ,n
对于第二个方程,求解最终结果xi:
其中xn = yn,其余各项的递推求解关系是:
xi = yi – uixi+1, i = n – 1, n – 2, …, 1
递推计算yi和xi的过程分别被形象地形容为追的过程和赶的过程,这也是追赶法得名的原因,实际上这种方法在国际上叫做托马斯(Thomas)法。在这里需要强调一下,对三角矩阵的克洛脱分解需要满足几个条件,否则无法进行,这几个条件分别是:
下面就给出一个追赶法求解方程组的通用算法实现,在使用之前需要判断系数矩阵是否是对三角矩阵,并且满足上述三个条件,相关的判断请读者自行添加:
|
76 /*追赶法求对三角矩阵方程组的解*/ 77 bool ThomasEquation::Resolve(std::vector<double>& xValue) 78 { 79 assert(xValue.size() == m_DIM); 80 81 std::vector<double> L(m_DIM); 82 std::vector<double> M(m_DIM); 83 std::vector<double> U(m_DIM); 84 std::vector<double> Y(m_DIM); 85 86 /*消元,追的过程*/ 87 L[0] = m_matrixA[ARR_INDEX(0, 0, m_DIM)]; 88 U[0] = m_matrixA[ARR_INDEX(0, 1, m_DIM)] / L[0]; 89 Y[0] = m_bVal[0] / L[0]; 90 for(int i = 1; i < m_DIM; i++) 91 { 92 if(IsPrecisionZero(m_matrixA[ARR_INDEX(i, i, m_DIM)])) 93 { 94 return false; 95 } 96 M[i] = m_matrixA[ARR_INDEX(i, i - 1, m_DIM)]; 97 L[i] = m_matrixA[ARR_INDEX(i, i, m_DIM)] - M[i] * U[i - 1]; 98 Y[i] = (m_bVal[i] - M[i] * Y[i - 1]) / L[i]; 99 if((i + 1) < m_DIM) 100 { 101 U[i] = m_matrixA[ARR_INDEX(i, i + 1, m_DIM)] / L[i]; 102 } 103 } 104 /*回代求解,赶的过程*/ 105 xValue[m_DIM - 1] = Y[m_DIM - 1]; 106 for(int i = m_DIM - 2; i >= 0; i--) 107 { 108 xValue[i] = Y[i] - U[i] * xValue[i + 1]; 109 } 110 111 return true; 112 } |
12.3.6 三次样条曲线拟合算法实现
根据12.3.4节对三次样条函数的推导分析,三次样条曲线拟合算法的核心可分为三部分,第一部分是根据推导结果计算关于三次样条函数的“矩”的方程组的系数矩阵,第二部分就是用追赶法求解方程组,得到各个区间的三次样条函数,第三部分就是根据每个拟合点的输入的值xi,确定使用哪个区间的三次样条函数,并使用该区间的三次样条函数计算出三次样条插值yi,最后得到的一系列(xi, yi)组成的曲线就是三次样条拟合曲线。拟合算法也是按照上面的分析,分三个步骤计算插值:
第一步是计算系数矩阵,其中u0、v0、d0和dn的值需要单独计算,其余的值可以通过(3.19)递推计算出来。
第二步是将系数矩阵代入12.3.5节给出的追赶法通用算法,求出Mi的值。求解之前,先证明一下第一步得到系数矩阵是否满足追赶法的条件。首先,主对角线元素的值都是2,满足12.3.5节的条件(1)。其次,由ui和vi的计算条件可知,|ui| < 1,|vi| < 1,这也满足12.3.5节的条件(2)。最后,因为ai = 2,且ui和vi的和是1,所以12.3.5节的条件(3)也得到了满足。由上判断可知,求解三次样条函数的“矩”的系数矩阵满足使用追赶法求解的条件,可以使用追赶法求解。
第三步是计算插值,需要将第二步计算得到的Mi代入(3.15),并选择合适的子区间样条函数计算出插值点的值。
下面就给出采用三弯矩法实现的三次样条曲线拟合算法,CalcSpline()函数的参数Xi和Yi是n个插值点(包括起点和终点)的值,boundType是边界条件类型,b1和b2分别是对应的两个边界条件,这个算法支持第一类和第二类边界条件(包括自然边界条件)。内部的矩阵matrixA就是按照(3.29)构造的Mi方程组的系数矩阵,可用于直接用追赶法求解方程组。CalcSpline()函数的大部分代码都是在构造Mi方程组的系数矩阵,首先根据边界条件确定un 、v0 、d0和dn,其他系数则根据(3.19)的递推关系,在for(int i = 1; i < (m_valN - 1); i++)循环中依次计算出来,最后是利用12.3.5节给出的追赶法算法求出Mi。GetValue()函数负责计算给定区间内任意位置的插值,首先根据x的值确定使用哪个子区间的样条函数,然后根据(3.12)和(3.14)给出的关系计算插值。
|
16 void SplineFitting::CalcSpline(double *Xi, double *Yi, int n, int boundType,double b1, double b2) 17 { 18 assert((boundType == 1) || (boundType == 2)); 19 20 double *matrixA = new double[n * n]; 21 if(matrixA == NULL) 22 { 23 return; 24 } 25 double *d = new double[n]; 26 if(d == NULL) 27 { 28 delete[] matrixA; 29 return; 30 } 31 32 m_valN = n; 33 m_valXi.assign(Xi, Xi + m_valN); 34 m_valYi.assign(Yi, Yi + m_valN); 35 m_valMi.resize(m_valN); 36 memset(matrixA, 0, sizeof(double) * n * n); 37 38 matrixA[ARR_INDEX(0, 0, m_valN)] = 2.0; 39 matrixA[ARR_INDEX(m_valN - 1, m_valN - 1, m_valN)] = 2.0; 40 if(boundType == 1) /*第一类边界条件*/ 41 { 42 matrixA[ARR_INDEX(0, 1, m_valN)] = 1.0; //v0 43 matrixA[ARR_INDEX(m_valN - 1, m_valN - 2, m_valN)] = 1.0; //un 44 double h0 = Xi[1] - Xi[0]; 45 d[0] = 6 * ((Yi[1] - Yi[0]) / h0 - b1) / h0; //d0 46 double hn_1 = Xi[m_valN - 1] - Xi[m_valN - 2]; 47 d[m_valN - 1] = 6 * (b2 - (Yi[m_valN - 1] - Yi[m_valN - 2]) / hn_1) /hn_1; //dn 48 } 49 else /*第二类边界条件*/ 50 { 51 matrixA[ARR_INDEX(0, 1, m_valN)] = 0.0; //v0 52 matrixA[ARR_INDEX(m_valN - 1, m_valN - 2, m_valN)] = 0.0; //un 53 d[0] = 2 * b1; //d0 54 d[m_valN - 1] = 2 * b2; //dn 55 } 56 /*计算ui,vi,di,i = 2,3,...,n-1*/ 57 for(int i = 1; i < (m_valN - 1); i++) 58 { 59 double hi_1 = Xi[i] - Xi[i - 1]; 60 double hi = Xi[i + 1] - Xi[i]; 61 matrixA[ARR_INDEX(i, i - 1, m_valN)] = hi_1 / (hi_1 + hi); //ui 62 matrixA[ARR_INDEX(i, i, m_valN)] = 2.0; 63 matrixA[ARR_INDEX(i, i + 1, m_valN)] = 1 - matrixA[ARR_INDEX(i, i - 1,m_valN)]; //vi = 1 - ui 64 d[i] = 6 * ((Yi[i + 1] - Yi[i]) / hi - (Yi[i] - Yi[i - 1]) / hi_1) /(hi_1 + hi); //di 65 } 66 67 ThomasEquation equation(m_valN, matrixA, d); 68 equation.Resolve(m_valMi); 69 m_bCalcCompleted = true; 70 71 delete[] matrixA; 72 delete[] d; 73 } 74 75 double SplineFitting::GetValue(double x) 76 { 77 if(!m_bCalcCompleted) 78 { 79 return 0.0; 80 } 81 if((x < m_valXi[0]) || (x > m_valXi[m_valN - 1])) 82 { 83 return 0.0; 84 } 85 int i = 0; 86 for(i = 0; i < (m_valN - 1); i++) 87 { 88 if((x >= m_valXi[i]) && (x < m_valXi[i + 1])) 89 break; 90 } 91 double hi = m_valXi[i + 1] - m_valXi[i]; 92 double xi_1 = m_valXi[i + 1] - x; 93 double xi = x - m_valXi[i]; 94 95 double y = xi_1 * xi_1 * xi_1 * m_valMi[i] / (6 * hi); 96 y += (xi * xi * xi * m_valMi[i + 1] / (6 * hi)); 97 98 double Ai = (m_valYi[i + 1] - m_valYi[i]) / hi - (m_valMi[i + 1] -m_valMi[i]) * hi / 6.0; 99 y += Ai * x; 100 double Bi = m_valYi[i + 1] - m_valMi[i + 1] * hi * hi / 6.0 - Ai * m_valXi[i+ 1]; 101 y += Bi; 102 return y; 103 } |
12.3.7 三次样条曲线拟合的效果
本节将用定义一个原始函数,从原始函数的某个区间上抽取9个插值点,根据这9个插值点和原函数的边界条件,利用三次样条曲线插值进行曲线拟合,并将原始曲线和拟合曲线做对比,展示一下三次样条曲线拟合的效果。
首先定义原始函数:
f(x) = 3/(1 + x2)
选择区间[0.0, 8.0]上的9个点做为插值点,计算各点的值为:
| x | 0.0 | 1.0 | 2.0 | 3.0 | 4.0 | 5.0 | 6.0 | 7.0 | 8.0 |
| y | 3.0 | 1.5 | 0.6 | 0.3 | 0.1765 | 0.1154 | 0.0811 | 0.06 | 0.0462 |
表 12 – 2 原函数f(x)在各插值点的值
求f(x)的导函数f’(x):
f’(x) = -6x/(1 + x2)2
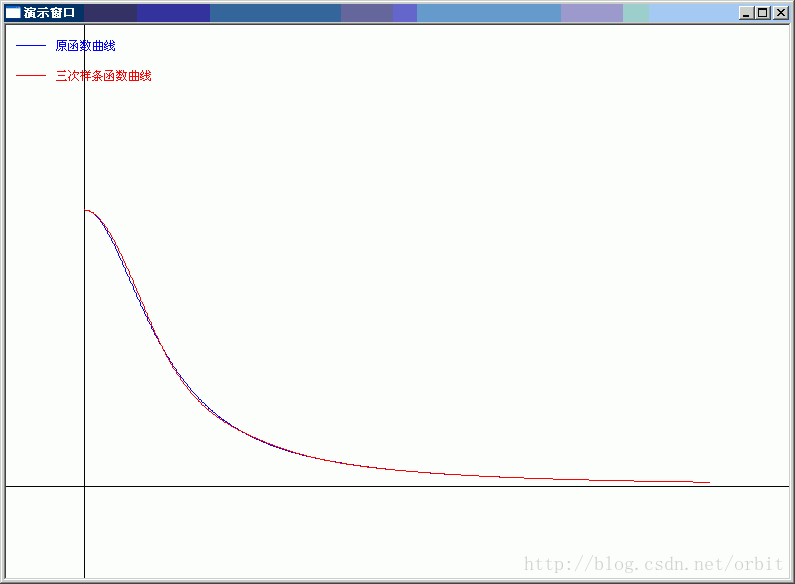
根据f’(x)计算出在区间端点处的两个第一类边界条件f’(0.0) = 0.0, f’(8.0) = -0.01136。利用表12-2中的数据和这两个边界条件,计算出三次样条插值函数,并从0.0开始,以0.01为步长,连续求800个点的插值,将这些点连成曲线得到拟合曲线。为了作对比,同样从0.0开始,以0.01为步长,用f(x)函数连续计算800个点的原值,将这些点连成曲线得到原始曲线。分别用不同的颜色画出这两条曲线,如图12-2所示:
图12-2 拟合曲线和原始曲线对比
从图12-2可以看到,三次样条曲线拟合的效果非常好。同样在[0.0, 8.0]区间上,如果增加插值点的个数,将获得更好的拟合效果。比如以0.5为单位,将插值点增加到17个,则拟合的曲线与原始曲线几乎完全重合。
网址:http://blog.csdn.net/kuikuijia/article/details/45405911









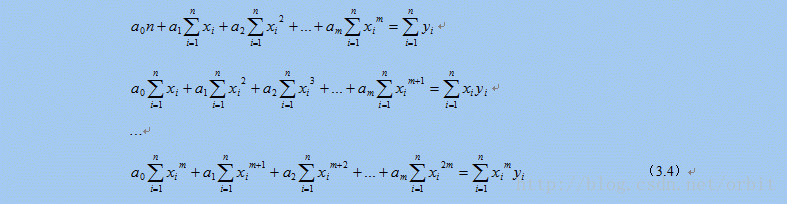




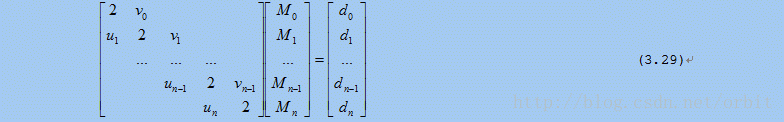

















 1785
1785

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








