

各位童鞋,今天咱们来复习一下数学。数学对于机器学习的重要性,怎么强调都不为过,我以前的某个朋友为了转行做机器学习,天天在推公式![]() 。本文将从线性方程组出发,引入矩阵。
。本文将从线性方程组出发,引入矩阵。
不要急着说,“你别讲了,矩阵的一切我都懂!”。先问问自己,是否知道什么是增广矩阵,LU分解,奇异矩阵

矩阵的一个重要来源是线性方程组。先看一个简单的2元线性方程组。

有两种方式看待线性方程组,即:“行图像”、“列图像”
行图像。
每个方程对应一条直线(超平面),即行图像。那么,方程组的解即为交点(当直线平行时则无解;重叠时则无穷解,奇异情况)。行图像并不是很好的思考方式,很难想象超平面的交点。
列图像。
线性方程组可以表示成:向量的线性组合。
这样就转化成 col1, col2 怎么转化为结果向量c。列图像是一种不错的思考方式,很容易扩充到高维空间。
可以将线性方程组写成矩阵形式。其中系数构成一个系数矩阵。
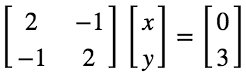
系数矩阵:
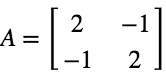
未知数向量:

结果向量:
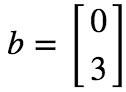
那么线性方程组就写成了“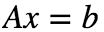 ”的形式。
”的形式。
恭喜,其实我们已经引入了矩阵乘法的概念,矩阵-向量乘法可以转化为 col 的线性组合。
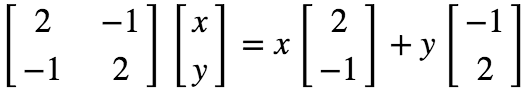
不难扩展为矩阵乘法(方法一:整列相乘)。
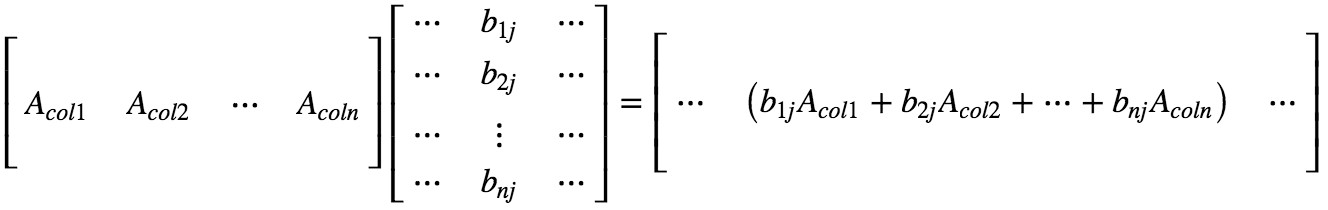
其中: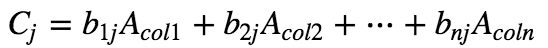
规则:C 的第 j 列可以表示为 A 的各个 col 与 B 的第 j 列的线性组合。
现在我们有两个待解决的问题:
1. 线性方程组如何求解?
2. 线性方程组一定有解?
先来解决第一个问题:线性方程组如何求解。思路其实小学就学过,可以采用“消元法”,最开始由高斯大爷发现的, 所以被称为“高斯消元法”。
看一个新例子:

写成矩阵的形式(静态形式):
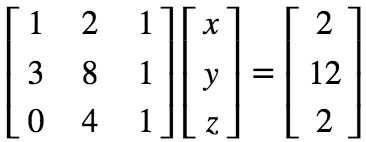
高斯消元法的主要思想:行变换不影响线性方程组的解。
主要分两步进行:消元 + 回代
1. 消元
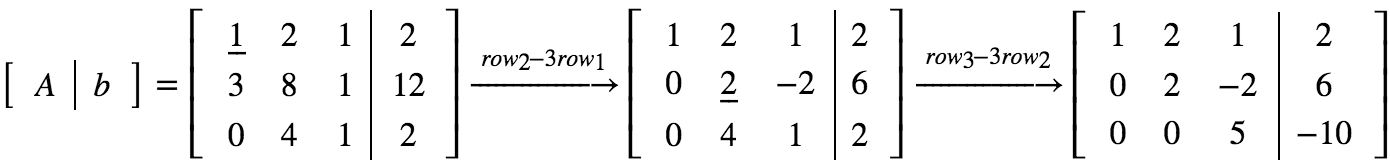
 被称为增广矩阵,消元就是在增广矩阵上不断进行行变换,直到矩阵 A 变为上三角矩阵。
被称为增广矩阵,消元就是在增广矩阵上不断进行行变换,直到矩阵 A 变为上三角矩阵。
行变换,需要每次选定一个主元(pivot),作为参考点,如上图 underline 数字就是 pivot。
2. 回代
通过行变换,最终变为:
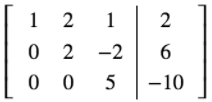
还原成方程组的形式就是:
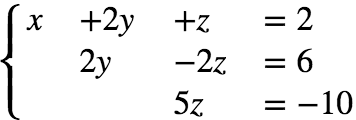
回代过程:利用方程3,得出 z = -2, 将 z = -2 代入方程2,得到 y = 1,再将 y,z 代入方程1,得出 x = 2。
一切好像很完美。但是依然会存在问题:
1. 消元时可能会导致主元为0,导致后续无法进行下去,可能你想到交换行就可以了,聪明。
2. 比如方程3 的 z 的系数改为-4。第 2 步消元后第三个主元不存在,高斯消元法彻底没戏(这种情况下讲会详细讲解)。
介绍之前,从“整行相乘”理解矩阵乘法(方法二:整行相乘)。
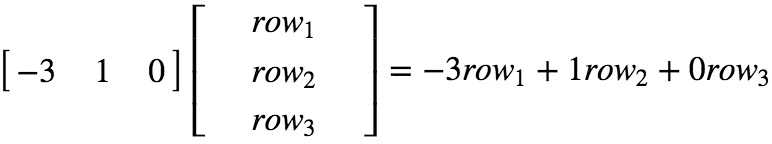
扩展之,
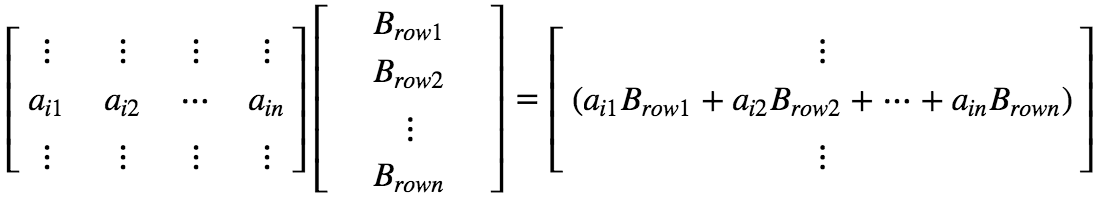
其中: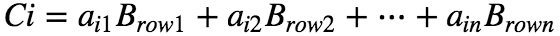
规则:C 的第 i 行可以表示为 A 的第 i 行与 B 的各个 row 的线性组合。
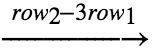 可以用矩阵表示:
可以用矩阵表示:
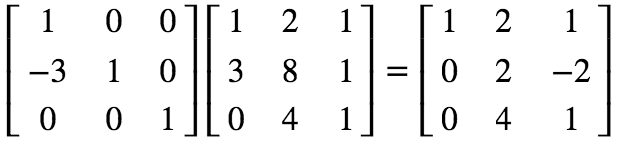
可以看出只是第 2 行发生了变化,可以看出矩阵可以描述变换(动态特性)。
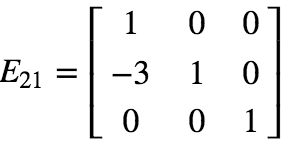
进行进行行变换,得到:

这个过程可以描述成: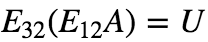 ,其中 U 为 上三角矩阵。由于矩阵乘法满足结合率,进一步写成:
,其中 U 为 上三角矩阵。由于矩阵乘法满足结合率,进一步写成: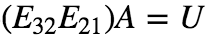
上节说到,消元过程中可能导致主元为0,这时就需要交换(置换)两行。依然可以用矩阵表示。
例如:
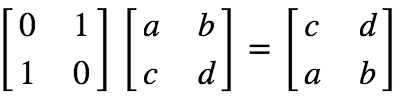
定义以下三种变换为初等变换:
1. 交换矩阵某两行(列)的位置。对应初等矩阵为:Pij。
2. 用一个非零常数 k 乘以矩阵的某一行(列)。对应初等矩阵为:Eα。
3. 将矩阵的某一行(列)乘以常数 k 后加到另一行(列)上去。对应初等矩阵为:Eij。
不难理解,每个初等变换都对应变换矩阵,称为初等矩阵。
上面例子,经过 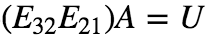 , 已经变成上三角矩阵,但这并不是最简形式,可以继续进行行变换(使用变换2和3,本例中未使用变换1)。
, 已经变成上三角矩阵,但这并不是最简形式,可以继续进行行变换(使用变换2和3,本例中未使用变换1)。

回代,直接就可以得出 x = 2, y = 1, z = -2。
不难发现,经过行变换,最终得到:单位矩阵 I (方阵的最简形式).
用矩阵形式表示这个过程:
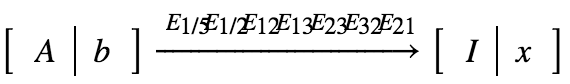
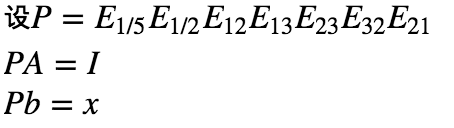
这样自然引入方阵的逆。
类比:
ax = b => x = a^-1 b(前提:x≠0)
Ax = b => x = A^-1 b(前提可逆)
这样方程组的解可以直接找到解析解。
方阵的逆
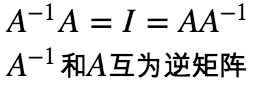
结论:
1. 方矩的左逆和右逆相同。简称方阵的逆矩阵。
2. 初等矩阵肯定有逆矩阵,因为初等矩阵肯定可以通过行变换变为单位矩阵。
3. 并不是所有方阵都有逆矩阵,没有逆矩阵的方阵被称为不可逆矩阵(通常情况方阵都是可逆的,不可逆矩阵是比较少的,所以被称为奇异矩阵)。

方法一:转化为方程组
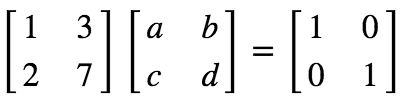
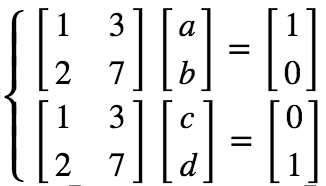
方法二:Gauss-Jordan 方法
其实和高斯消元法思路差不多。
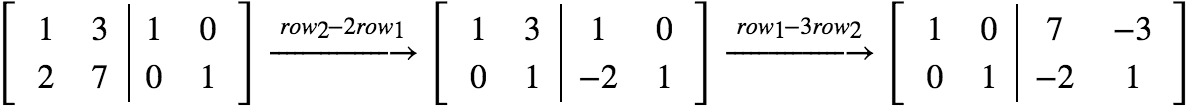
思想: [ A | I ] → [I | P]。利用 I 跟踪行变换的整个过程,最终变换矩阵就是逆。
A 经过行变换变为 I,用矩阵表示,就是存在一个矩阵P,使得 P A = I,显然 P 就是我们要求的 A 的逆(根据定义)。与此同时,I 经过行变化变为:P I = P(跟踪行变换)。
作为行变换的副产品。如果 A 经过行变换变为 U。即 P A = U。
则 A = P^-1 U
不难发现,变换过程采用的都是下三角矩阵,所以 P 也是下三角矩阵,P 的逆也是下三角矩阵,记为 L = P-1。
这就是传说中的方阵的 LU 分解。
任何可逆的方阵均可分解为: A = L U
这个结论有缺陷。就是没有考虑可能需要行交换。这样就引入了置换矩阵的概念。
定义:单位矩阵进行任意有限次行变换后的矩阵称为置换矩阵,通常记为 P。
显然 n 阶矩阵 有 n! 个置换矩阵。比如:3 阶方阵对应如下 6 个置换矩阵。
性质:置换矩阵的逆矩阵是其转置矩阵(自行百度转置)。
LU 分解的完整形式
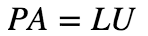
其中 P 为置换矩阵。
本文转载自我师弟的公众号,在此谢过!








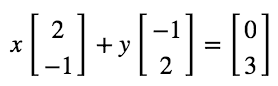
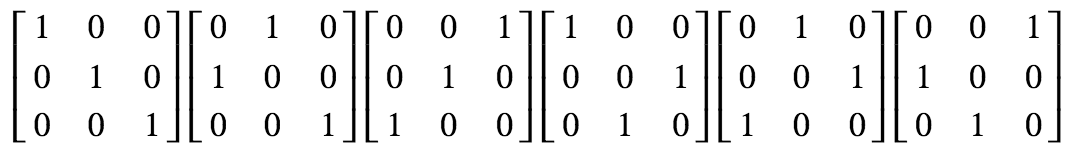
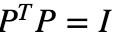













 5647
5647











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








