PCA－Principal Components Analysis数学原理

最新推荐文章于 2024-04-07 10:32:01 发布
原创 最新推荐文章于 2024-04-07 10:32:01 发布 · 5.6k 阅读 · 9 ·
CC 4.0 BY-SA版权
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
文章标签：

#机器学习 #数学

PCA（主成分分析）用于处理高维数据，通过线性变换减少特征冗余。本文深入探讨PCA的动机、定义、相关知识、处理流程及特征值的重要性，揭示PCA如何增强数据的表征能力并进行有效的降维。 
转载请注明出处：blog.csdn.net/yobobobo

最近自学的重点是特征工程，首当其冲的当然是PCA，可是看了好几篇国内搜索靠前的博客大部分都是做法而不是原理，为什么协方差矩阵的特征值最大就说明投影到这个特征向量上比其他的好呢？对于机器学习大部分时间都是调用别人写好的库就像是个用着黑盒子的感觉，特来一发原理，附上完整的数学推导。

Motivation———PCA的作用是什么，我们为什么要用PCA

  • 你手上有一批数据，但是特征太多，你感觉数据太稀疏了

  • 你选了一堆特征，但是感觉某些特征之间的相关性太高了，比如用户月消费预测的时候，你选了用户身高以及用户性别这两个特征，一般男生的身高比较高，你觉得特征有点冗余

  • 你的小霸王内存不够，内存只有4个G，装不下太大的矩阵，但是你又不想减少训练数据，N＊M的数据集，你不想减少N，下一步只有减少M了

  • 你想减少M了，可是你又不知道哪些特征该扔掉，就算你选出了一些看起来不是那么好的特征扔掉你又怕这些特征扔掉后对模型的影响很大

Definition———PCA是啥？

  • wiki翻译－－－－PCA是一门数据统计方案，通过一个正交转换把可能线性相关的变量转换为几乎线型无关的变量（这些变量称作主成分）。主成分的数量比原来的变量数量更少或者一致。
  • 通俗地讲，PCA就是把N维的向量经过线型变换转化为K维的向量（K<=N），需要注意的是，并不是把N－K维的特征扔掉了。
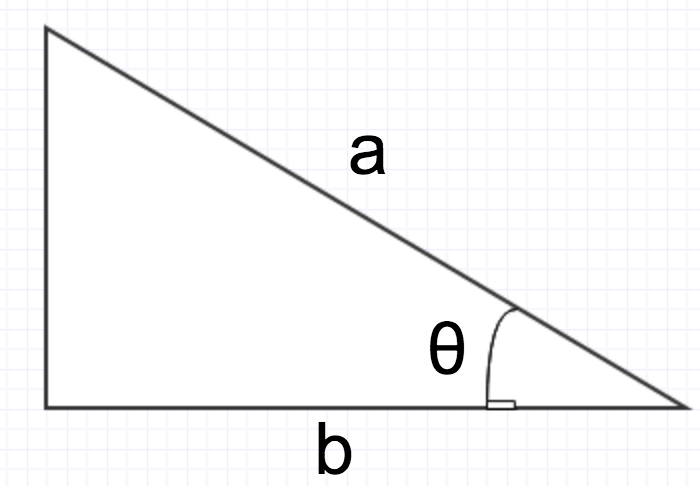
  • 向量点积的几何意义
    • a∗b=∥a∥∗∥b∥∗cosθ
    • Drawing
    • ∥a∥∗cosθ 相当于把a投影到b向量上的长度 当 ∥b∥ 为1的时候,a＊b就相当于把a投影到向量b上的长度
  • 协方差矩阵
    • 方差足够了吗？
    • 以前上小学的时候，老师经常把某个学生的成绩记录作为讲解方差的经典例子，A的成绩均值和B的成绩均值一样，这时候怎么区分谁更好呢？
    • 答日：A的方差比B的方差更小，说明A的成绩更加稳定。
    • 然而这是小学，处理一维的数据已经足够了。
    • 现实中的数据都是远远超过一维的，现在广告推荐的大规模LR训练特征可达上亿维度，方差已经不能再像以前一样：“较均值，取方差”。
    • 协方差登场
    • 定义： cov(a,b)=∑ni=1(Xi−X⎯⎯)(Yi−Y⎯⎯)n−1
    • 意义：表示两个数据的线型相关性，当 cov(a,b) > 0的时候，说明 a 和 b 的是正相关的， a 越大 b 越大，反之时负相关的，为0则说明两者线型无关。
    • 协方差矩阵
      顾名思义，就是不同变量之间的协方差组成的矩阵
      cov(a,a)cov(b,a)cov(c,a)cov(a,b)cov(b,b)cov(c,b)cov(a,c)cov(b,c)cov(c,c)

Main Process———处理流程

  • 均值置0，把每一维度的特征都减去该维特征的均值，为了接下来的运算以及解释方便点
  • 求出数据集X的协方差矩阵M
  • 求解M的特征值对角阵以及特征向量矩阵
  • 选取前K大的特征值，将其对应的特征向量作为列向量，组成一个矩阵T
  • X＊T，得到降维之后的矩阵，完毕。

Why———为什么特征值这么神奇

  • 核心：方差越大，数据的表征能力越强
    • 给你两组数据，一组数据基本集中于某个点，另一组数据零零散散的，你认为哪个数据更好？一般都认为后者更好，因为前者可能是数据太少了，数据都集中于某一个点，这样的数据训练出来的模型泛化能力很差，后者的数据可以认为比较样本空间覆盖度高，训练出来的模型泛化能力更强。
    • 从上一个例子，我们可以认为：方差越大，数据的表征能力越强

详细———线型变换

  • 我认为当前数据的方差还不够大，可以把数据投影到另一个向量空间后以增大数据的方差，提升数据的表征能力
  • 根据第3节，数据投影可以表示为乘以一个模为1的向量，根据方差最大的思想，可以得到这样的目标函数
    • w(1)=
最低0.47元/天 解锁文章
PCA的数学原理
weixin_40994552的博客
03-29 1025
PCA的数学原理1 奇异值分解 SVD协方差矩阵2 PCA 原理参考 1 奇异值分解 SVD 任何 m×nm×nm×n 实矩阵 A, A∈Rm×nA ∈R^{m×n}A∈Rm×n 的奇异值分解一定存在，表示为三个矩阵的乘积： A=UΣVT A=UΣV^\mathsf{T}A=UΣVT 其中 U 是 m 阶正交矩阵，V 是 n 阶正交矩阵; Σ 是 m×n 矩形对角矩阵，其对角线元素称为奇异值，值非负，且按降序排列，这种分解方式称为矩阵的完全奇异值分解 在实际应用中，SVD 被用来对矩阵做近似表示，也即 UΣ
PCA(主成分分析-principal components analysis)学习笔记以及源代码实战讲解
梁先森的博客
05-04 1987
在看完吴恩达讲解的PCA(主成分分析)方法后，想着能够用代码的方式实践一下。紧接着就借阅了一下《机器学习实战》里面对PCA的流程的讲解和代码。现在对PCA的运算过程还是比较明白的，也希望这份学习笔记能够帮助刚开始学习PCA的同学们。
PCA数学原理详解
06-16
PCA是一种常用的数据降维方法，这里具体介绍了它的降维原理即降维的数学原理，通过这个学习我们能更好的了解PCA
pca的数学原理
03-08
如果你想学习pca，这个请不要错过
PCA以及降维的思想
子穹的专栏
04-26 2534
PCA（Principal Component Analysis）是一种常用的数据分析方法。PCA通过线性变换将原始数据变换为一组各维度线性无关的表示，可用于提取数据的主要特征分量，常用于高维数据的降维。网上关于PCA的文章有很多，但是大多数只描述了PCA的分析过程，而没有讲述其中的原理。这篇文章的目的是介绍PCA的基本数学原理，帮助读者了解PCA的工作机制是什么。 当然我并不打算把文章写成
机器学习（2）——PCA（principal components analysis 主成分分析）降维
qq_41921709的博客
02-20 863
概念 PCA（principal components analysis）即主成分分析技术，又称主分量分析。主成分分析也称主分量分析，旨在利用降维的思想，把多指标转化为少数几个综合指标。 在统计学中，主成分分析PCA是一种简化数据集的技术。它是一个线性变换。这个变换把数据变换到一个新的坐标系统中，使得任何数据投影的第一大方差在第一个坐标(称为第一主成分)上，第二大方差在第二个坐标(第二主成分)上，...
A tutorial on Principal Components Analysis.pdf
05-16
主成分分析（Principal Components Analysis，简称PCA）是一种广泛应用于多个领域的统计技术，包括但不限于人脸识别与图像压缩等高维数据处理场景。本教程旨在帮助读者理解PCA的基本概念及其应用场景。 PCA是一种...
PCA（Principal Component Analysis，主成分分析）
qlkaicx的博客
04-07 1666
总的来说，PCA是一种强大的数据分析工具，它通过降维技术将高维数据转化为低维表示，同时保留数据的主要特征。其工作原理基于线性代数和统计学的理论基础，通过计算协方差矩阵、特征值分解等步骤实现数据的降维和信息的提取。
Machine Leanring-Principal Component Analysis(PCA)
BD的笔记
06-12 3253
Principal Component Analysis 方差：数据与平均数之差平方和的平均数。更多详见 Principal Component Analysis(PCA)是最常用的线性降维方法，它的目标是通过某种线性投影，将高维的数据映射到低维的空间中表示，并期望在所投影的维度上数据的方差最大，以此使用较少的数据维度，同时保留住较多的原数据点的特性。通俗的理解，如果把所有的点都映射到一起，那么几
PCA（主成分分析）的数学原理(之前一门课程写的报告,现在发上来...)
lovemylife1234的博客
05-04 2327
1.背景介绍 一般情况下，在数据挖掘和机器学习等数据分析领域中，数据都被表示为向量。众所周知，很多机器学习算法的复杂度和数据的维数有着密切关系，甚至与数据维数呈指数级别关联。然而实际机器学习中处理的数据可达成千上万甚至几十万维，在这种情况下，算法的资源消耗是不可接受的，因此我们必须对数据进行降维。PCA（Principal Component Analysis），即所谓的主成分分析，...
PCA的数学原理（转）
wyisfish的博客
06-05 699
首先我们直接给出PCA算法步骤： 设有m条n维数据。 1）将原始数据按列组成n行m列矩阵XXX 2）将X的每一行（代表一个特征字段）进行零均值化，即减去这一行的均值 3）求出协方差矩阵C=1mXXTC=1mXXTC=\frac{1}{m}XX^{T} 4）求出协方差矩阵的特征值及对应的特征向量 5）将特征向量按对应特征值大小从上到下按行排列成矩阵，取前k行组成矩阵P 6）Y=PXY=...
PCA数学原理
u012005313的专栏
03-13 2373
转载自：http://www.360doc.com/content/13/1124/02/9482_331688889.shtml# ############################################################# PCA(Principal Component Analysis)是一种常用的数据分析方法。PCA通过线性变换将原始数据变
PCA数学原理解析
qq_34355221的博客
10-14 324
PCA主成分分析，主要用于多维数据的降维。 降维当然意味着信息的丢失，不过鉴于实际数据 本身常常存在的相关性，我们可以想办法在降维的同时将信息的损失尽量降低。 PCA算法的主要步骤： 1、每一行为一个字段，每一列为一个数据 2、均值为零，使得协方差矩阵的主对角线上的数为n个维度各自对应的方差 3、协方差矩阵为实对称矩阵，所以可以相似对角化 4、协方差矩阵不同特征值对应的特征向量必然正交，r重特...
PCA（主成分分析）
zs_id的博客
12-31 6817
PCA的主要思想是将n维特征映射到k维上，这k维是全新的正交特征也被称为主成分，是在原有n维特征的基础上重新构造出来的k维特征。∑是一个m∗n的矩阵，∑除了对角线其它元素都为0，对角线上的元素称为奇异值。VT是V的转置矩阵，是一个n∗n的矩阵，它里面的正交向量被称为右奇异值向量。通过计算数据矩阵的协方差矩阵，然后得到协方差矩阵的特征值和特征向量，选择特征值最大(即方差最大)的k个特征所对应的特征向量组成的矩阵。其中，Q是矩阵A的特征向量组成的矩阵，Σ则是一个对角阵，对角线上的元素就是特征值。
基于主成分分析（PCA, Principal Component Analysis）用于智能运维异常检测的算法基本原理
最新发布
05-12
<think>好的，我现在需要回答用户关于基于PCA的智能运维异常检测算法的基本原理的问题。首先，我得回顾一下PCA的基础知识，以及它在异常检测中的应用。 主成分分析（PCA）是一种常用的降维技术，通过线性变换将高维数据投影到低维空间，保留主要特征。在智能运维中，异常检测通常涉及处理高维时序数据，比如服务器指标、日志数据等。用户提到智能运维，可能涉及引用[4]中的归因分析和根因分析，以及引用[5]中提到的处理高维数据的方法。 首先，PCA的基本原理是将数据投影到方差最大的几个主成分上，减少维度同时保留大部分信息。在异常检测中，正常数据通常在主成分上有较高的投影，而异常可能分布在较低方差的方向上。所以，重建误差（原始数据与重建数据之间的差异）可能作为异常评分。 接下来，我需要结合引用中的内容。引用[3]提到基于正常数据的特征进行异常检测，这与PCA的思路类似，即利用正常数据的主成分特征来判断异常。引用[5]也提到使用PCA等降维技术减少计算开销，这可能与处理高维运维数据相关。 然后，需要具体说明PCA在异常检测中的步骤：数据标准化、计算协方差矩阵、特征分解得到主成分、选择k个主成分、计算重建误差作为异常分数。这里可能需要数学公式，比如重建误差的计算，用LaTeX表示，如$$ \text{Reconstruction Error} = ||\mathbf{x} - \mathbf{U}_k\mathbf{U}_k^T\mathbf{x}||^2 $$，其中$\mathbf{U}_k$是前k个特征向量组成的矩阵。 还要考虑引用[1]中提到的降维技术的工程目标，如处理高维数据痛点，PCA在这里的作用是降低维度，同时保留主要结构，便于后续异常检测。引用[2]提到的算法模型注册和预处理算法可能涉及PCA作为预处理步骤，比如在特征提取阶段使用。 需要确保回答结构清晰，分步骤解释，并引用相关引用内容。例如，在解释重建误差时，可以提到引用[3]中的基于正常数据特征的方法，或引用[5]中处理高维数据的建议。此外，用户的问题可能关注智能运维的具体应用，所以需要结合运维场景，如监控指标中的异常点检测，减少误报（如引用[4]中的归因分析）。 最后，生成相关问题时要围绕PCA在异常检测中的扩展，比如参数选择、与其他方法对比、实际案例等，参考引用中的降维方法对比（引用[1]）和根因分析（引用[4]、[5]）。</think>基于主成分分析（PCA）的智能运维异常检测算法原理可分为以下核心步骤： ### 一、数据标准化预处理 对多维运维指标（CPU、内存、网络流量等）进行标准化处理： $$ \tilde{x}_i = \frac{x_i - \mu_i}{\sigma_i} $$ 确保各维度数据具有可比性，避免量纲差异导致主成分偏移[^1] ### 二、主成分空间构建 1. 计算协方差矩阵： $$ \Sigma = \frac{1}{n-1}X^TX $$ 2. 特征值分解获取主成分方向： $$ \Sigma = U\Lambda U^T $$ 3. 选择前k个最大特征值对应特征向量构建投影矩阵$U_k$，保留85%-95%方差贡献率[^5] ### 三、异常检测机制 1. **重建误差计算**： $$ \text{Error} = ||x - U_kU_k^Tx||_2^2 $$ 异常点在低方差方向上的投影会导致较大重建误差[^3] 2. **统计量构建**： - Hotelling's T²统计量监测主成分空间异常： $$ T^2 = x^TU_k\Lambda_k^{-1}U_k^Tx $$ - SPE（Squared Prediction Error）统计量捕获残差空间异常[^1] ### 四、阈值判定 采用核密度估计或极值理论设定动态阈值，超过阈值的样本判定为异常。该方法特别适合检测多维指标间的关联异常，如服务器多个性能指标的协同偏离[^4] ```python from sklearn.decomposition import PCA from sklearn.preprocessing import StandardScaler def pca_anomaly_detect(data, explained_variance=0.95): # 标准化 scaler = StandardScaler() scaled_data = scaler.fit_transform(data) # 自适应选择主成分 pca = PCA(n_components=explained_variance) pca.fit(scaled_data) # 计算重建误差 transformed = pca.transform(scaled_data) reconstructed = pca.inverse_transform(transformed) errors = np.linalg.norm(scaled_data - reconstructed, axis=1)**2 return errors ```
评论 5
成就一亿技术人!
拼手气红包6.0元
还能输入1000个字符
 
红包 添加红包
表情包 插入表情
表情包 代码片
 条评论被折叠 查看
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值