让我们首先谈一些监督学习问题的例子。假定我们有一个数据集,数据集中给出了来自俄勒冈波特兰的47所房子的居住面积(living areas)和价格(price):
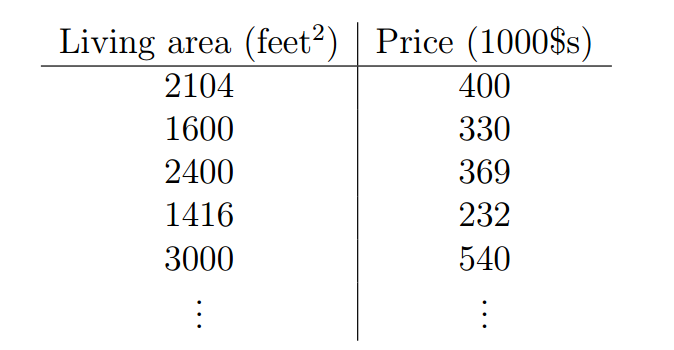
我们可以将这些数据标识于图表上:
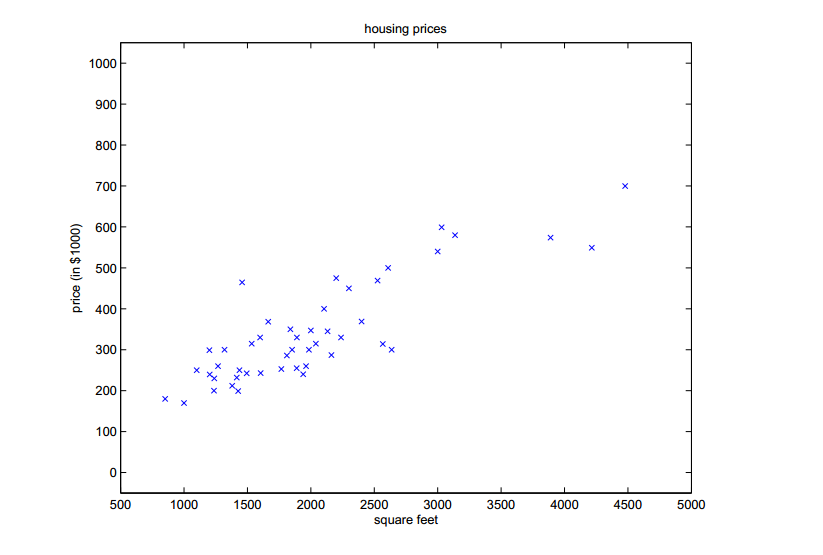
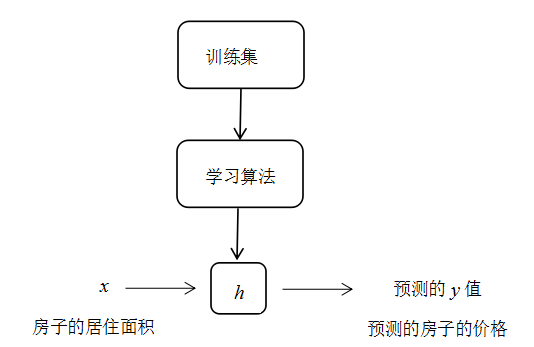
给定这样的数据,我们如何学习基于居住面积的大小的函数,来预测波兰特其它房子的价格。
为了建立以后使用的符号,我们使用
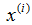 表示“输入”变量(这个例子中的居住面积),也被称作输入特征,
表示“输入”变量(这个例子中的居住面积),也被称作输入特征,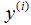 表示我们尽力预测的“输出”或者目标变量(价格)。一组
表示我们尽力预测的“输出”或者目标变量(价格)。一组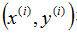 被称作一个训练例子,我们将要用来学习的数据集——m个训练例子
被称作一个训练例子,我们将要用来学习的数据集——m个训练例子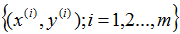 ——被称作一个训练集。注意符号中的上标
——被称作一个训练集。注意符号中的上标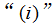 仅仅是一个指向训练集的索引,和指数没有关系。我们使用表示输入值的空间,表示输出值的空间。在这个例子中,
仅仅是一个指向训练集的索引,和指数没有关系。我们使用表示输入值的空间,表示输出值的空间。在这个例子中,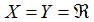 。
。为了稍微更加正式的描述监督学习问题,我们的目标是在给定一组训练集的情况下,学习一个函数
 ,
,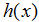 是一个对相对应值的好的预测器。由于历史原因,这个函数
是一个对相对应值的好的预测器。由于历史原因,这个函数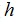 被叫做一个假设。可以形象地看出,过程就像这样:
被叫做一个假设。可以形象地看出,过程就像这样:
当我们正努力预测的目标变量是连续时,正如在我们房子的例子中,我们成这种学习问题为一个回归问题。当
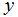 只能取少量的离散值时(比如,如果给定居住面积,我们想预测一个住处时一个house还是一个apartment),我们把它称作一个分类问题。
只能取少量的离散值时(比如,如果给定居住面积,我们想预测一个住处时一个house还是一个apartment),我们把它称作一个分类问题。
第一部分 线性回归
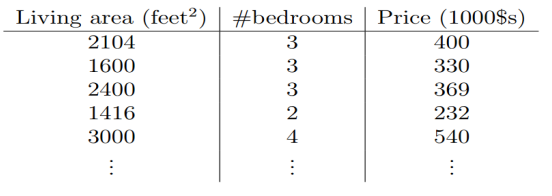
为了使我们的房子案例更有趣,让我们考虑一个更加丰富的数据集,在这个数据集里我们还知道每个房子里的卧室的数量:
这里,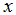
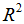
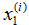
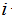
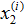
为了进行监督学习,我们必须决定我们将如何在电脑里表示函数/假设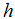
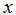
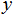
这里,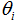
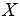
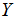
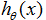
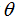
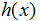

在上式的右端项我们把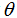
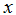
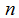

现在,给定一个训练集,我们如何选择或者学习参数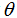
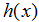
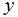
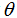
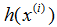
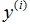
如果你之前看过线性回归,你可以认出这是熟悉的最小二乘代价函数,它引出了普通最小二乘回归模型。无论你之前是否看过线性回归,让我们继续,我们最终会说明这是一个更宽广算法家族的一种特殊情况。
1 LMS( Least mean square,最小均方)算法
我们想选择







(这个更新是对所有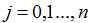
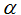
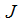
为了执行这个算法,我们必须算出右边的偏导数项是什么。让我们首先计算我们只有一个训练样本
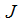
对于一个训练样本(的情况),给出更新规则:
这条规则被称作LMS更新规则(LMS代表“最小均方”),也被叫做widrow-hoff学习规则。这条规则有一些看起来很自然和直观的特征。比如,更新的量级和误差项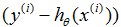



我们已经得到了当只有一个训练样本的LMS规则。对于多于一个训练样本的训练集,有两种方式可以修改这个方法。第一种方法是用以下的算法替换它:
重复直到收敛{
}
读者可以很简单证明上面更新规则中的求和量就是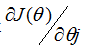
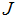
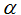
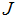
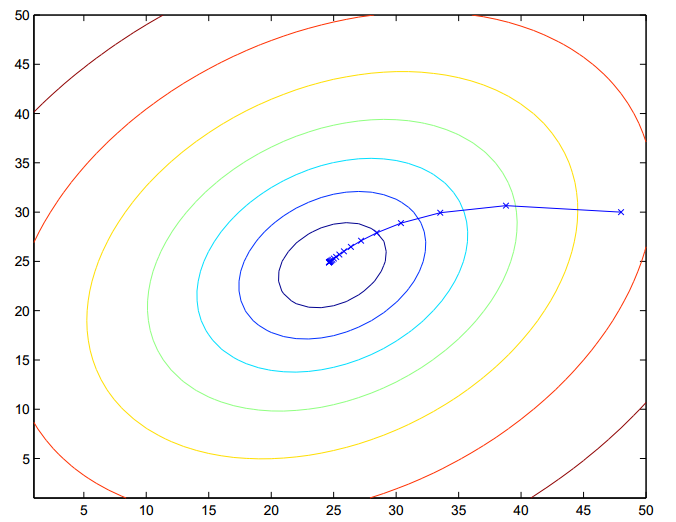
上面显示的椭圆形是一个二次函数的轮廓。梯度下降的轨迹也被显示了,初始值(48,30)。图形中x(叉号,被直线连接的)标记着梯度下降经过的连续的
为了学习预测房子价格的关于居住面积的函数,当我们对原来的数据集运行批梯度下降来寻求恰当的
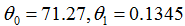
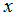
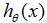
如果卧室的数量也被包含成为一个输入特征,我们得到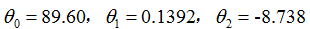
上面的结果是通过块梯度下降得到的。还有一种可以替代块梯度下降也工作不错的的算法。考虑以下的算法:
Loop{
For i=1 to m,{
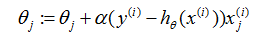
}
}
在这个算法中,我们反复地遍历训练集,每次我们针对一个训练样本。我们根据只基于单个训练例子的误差的梯度来更新参数。这个算法被称作随机梯度下降(也称作增量梯度下降)。批梯度下降在走一步之前必须扫描整个的训练集——如果m值太大的话,就是代价很高的操作——然而随机梯度下降可以立即前进,然后通过看每一个例子继续前进。经常,随机梯度下降得到接近最小值的远比批梯度下降更快。(注意到尽管它可能永远收敛不到最小值,参数

2 正规方程
梯度下降给了一种最小化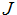
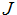
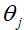
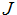
2.1 矩阵的导数
对于一个函数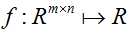
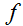

因此,梯度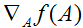
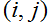
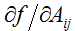
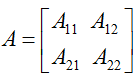
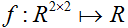
这里,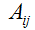


我们也引入运算符迹,写作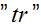


如果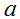
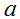
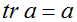

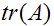

迹运算符有这样的特征,对于两个矩阵
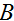
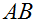
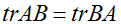
作为这个的推论,我们还可得到,比如,
迹运算符的一下特征也同样容易证明。这里,
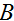
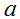
我们现在不加证明的陈述一下矩阵导数的一些事实(我们直到本节的晚些时候才需要它们中的一些)。等式(4)只应用于非奇异方阵


为了使我们的矩阵符号更具体化,让我们现在详细的解释一下这些等式中的第一个式子的意义。假定我们有某个固定的矩阵
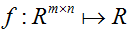
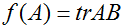
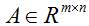
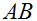
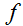


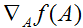

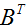


等式(1-3)的证明相当简单,给读者留作习题。等式(4)可以通过矩阵逆的伴随矩阵表示得到。
2.2 最小二乘再回顾
有了矩阵导数的工具,让我们继续求解使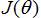
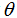

给定一个训练集,定义一个m x n的设计矩阵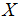
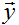
现在,因为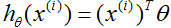
因此,使用关于向量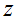

最后,为了最小化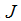
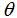
因此,
在第三步中,我们使用了一个实数的迹就是这个实数的事实;第四步使用了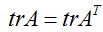
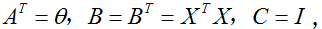
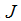
因此,使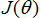
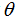
接下来讲到线性回归的概率解释和局部加权线性回归,详见下一讲。
想写一写机器学习的翻译来巩固一下自己的知识,同时给需要的朋友们提供参考,鉴于作者水平有限,翻译不对或不恰当的地方,欢迎指正和建议。





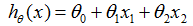
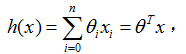
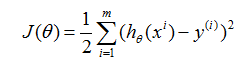
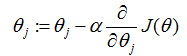
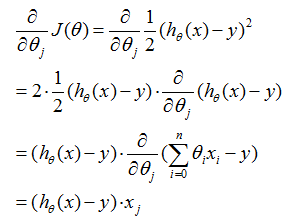
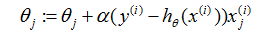
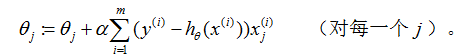

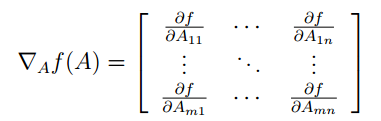
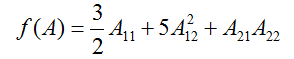
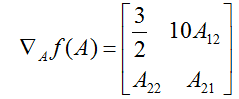
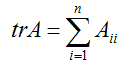
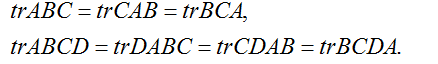

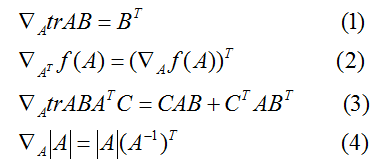
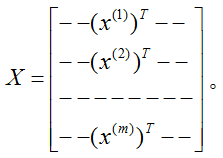
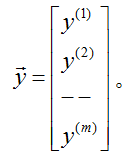
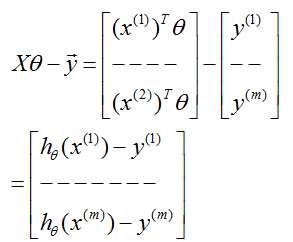

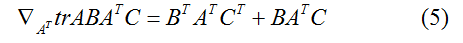
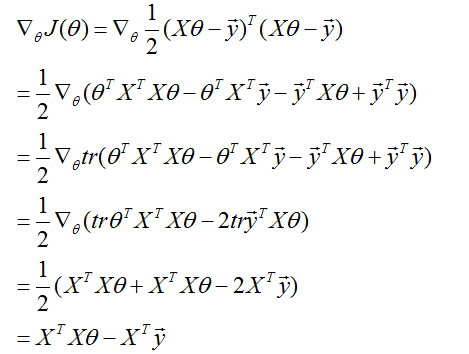
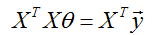
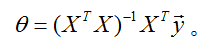
















 3304
3304

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








