T-lnP图绘制

Chen learner

于 2024-11-01 03:19:59 发布

阅读量3.1k

点赞数 21

文章标签：算法 python matplotlib

本文链接：https://blog.csdn.net/2201_75862806/article/details/143421041

版权

最近在研究T-lnP图的绘制，顺带着复习了一下各个相关参量的计算方法和原理。包括位温(θ)，假相当位温(θse)，饱和比湿(qs)，饱和水汽压（es）。国内传统的T-lnP图不同国外的skew-T（斜T-lnP图），即将T-lnP的等温线顺时针旋转45°。

什么是T-lnP图

T-lnP图，全称温度对数压力图解，又称为埃玛图（Emagram），是目前我国各气象台站广泛使用的图解。横轴表示气温，纵轴表示气压的对数值。图中通常包含干绝热线（等位温θ线，单位：℃）、湿绝热线（等假相当位温θse线，单位：℃）、等饱和比湿线（单位：g/kg）。干湿绝热线分别代表气块做干绝热运动和可逆的湿绝热过程。

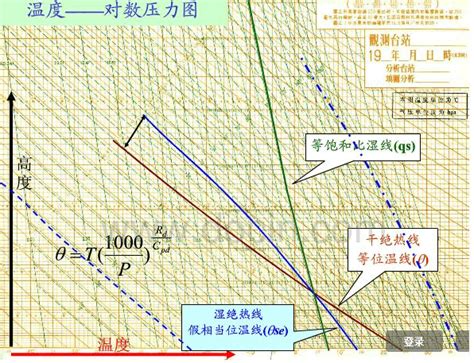
图中，黄色实斜线为干绝热线，绿色斜实线为等饱和比湿线，绿色斜虚线为湿绝热线。

绝热过程

绝热过程指在改变某个系统的物理状态（压强、体积或温度）时，系统与环境间无热量交换，但可以有功的交换。

干绝热过程

干绝热过程是指干空气在状态变化（ P,V,T ）过程中与外界既无热量交换也无质量交换的过程。对于未饱和湿空气来说，只要上升过程中未达到饱和，其状态变化也基本服从于干绝热过程。

位温

气块按干绝热过程移至标准气压（ p0=1000hPa）时气块所具有的温度，又称位势温度θ，常用绝对温度（K）表示。位温具有保守性，即沿干绝热上升下沉位温不变。

其中，κ＝R/cp≈0.286，公式由干空气状态方程推导而出。cp是比定压热容，R是气体常数。

湿绝热过程

可逆湿绝热过程

气块绝热上升时全部凝结水都留在气块内，随气块一起上升，当气块从上升运动转为下降时，绝热增温引起水滴蒸发，仍热沿着绝热过程回到原点，该过程是可逆的，称为可逆湿绝热过程。在这种情况下只有云而无降水。这实际是一种极端情况，即气块运动时无水汽脱离。

假绝热过程

与上述情况完全相反，为另一个极端情况，气块上升时所产生的全部凝结水以降雨的形式脱离气块，这样当气块从上升转为下沉时，绝热增温使得气块呈不饱和状态。由于气块上升过程是湿绝热过程，下沉时为干绝热过程，这是一个开放系的不可逆过程。而且，由于凝结物脱离了气块，气块与外界发生了能量交换，不是严格绝热的。因此认为气块经历了一次假绝热过程。这种极端情况全是降水而没有云。焚风是假绝热过程的典型例子。

饱和水汽压

水汽达到饱和时的水汽压强。是计算假相当位温中很重要的一个参数。

比湿

比湿 q为单位质量湿空气内的水汽质量，常用单位为 g/kg ，为绝对湿度参量，表达式为：

其中ϵ=Rd/Rv=0.622

饱和比湿

水汽压达到饱和水汽压时对应的比湿，可将上式中的e带入es计算得出。

露点

露点 Td为不改变气压 p 和混合比 w （既无凝结也无蒸发）的情况下，湿空气冷却达到饱和时的温度， Td<=T 。在露点温度下，湿空气的混合比等于饱和混合比，比湿等于饱和比湿。

以上的参量都是用来绘制T-lnP重要参数。为接下来的代码提供了参考。

大气的静力稳定度

抬升凝结高度 (LCL)

抬升凝结高度指未饱和湿空气绝热抬升至相对于平纯水面饱和时所达到的高度。

可由z=1÷(yd-ys)×(T-Td)算出，yd、ys、T、Td分别为干绝热递减率，湿绝热递减率，温度、露点温度计算出。在T-lnp图中表示为地面露点对应的等饱和比湿线与地面温度沿干绝热线上升的交点。

自由对流高度(LFC)

LFC(Level of Free Convective)是指空气团在升起过程中，温度降低到与周围环境温度相等的高度。此时，空气团开始自由对流，形成对流云。在T-lnp图中表示为气块的状态曲线和大气的层结曲线的第一个交点确定。与之对应的还有平衡高度D，为第二个交点，即温度等于环境温度时的高度。

对流凝结高度(CCL)

CCL(Convective Condensation Level)是指在气团升起时，空气冷却到露点温度并开始凝结的高度。在T-lnp图中表示为地面露点对应的等饱和比湿线与大气层结曲线的交点。

对流有效势能(CAPE)

CAPE(Convective Available Potential Energy)表示在对流中可用的能量。即状态曲线和层结曲线在LFC和D之间围成的正面积区的面积。

对流抑制能量(CIN)

CIN(Convective Inhibition)表示在气团上升过程中所遇到的能量障碍。是LFC和地面之间的状态曲线和层结曲线围成的负面积区的面积。

热对流下限温度(TCON)

热对流下限温度是指气团在上升过程中，温度与环境温度相等的点的温度。是CCL处沿干绝热下降到地面(1000hpa)对应的温度。它代表了气团必须达到的温度，以克服环境的稳定性并启动对流过程。对热雷雨的预报起到了重要作用。

以上的参量都是用来判断大气静力稳定度的重要参数。为接下来的代码提供了参考。

T-lnP绘制

接下来就是T-lnP图的绘制，本篇使用自定义的温度和气压算出各个温度和气压下的位温，假相当位温和等饱和比湿的分布。

代码部分

class T_lnp():
    def theta_cal(self,tem,p):#计算位温
        tem=tem+273.15#换算成k
        theta=np.ones([len(tem),len(p)])
        for i in range(len(tem)):
            for j in range(len(p)):
                theta[i,j]=tem[i]*(1000/p[j])**0.286 #(R / cp)
        theta=theta-273.15#换算为摄氏度
        return np.round(theta,1)
    def equal_saturation_q(self,tem, p):#计算等饱和比湿
        mask1 = (tem >= 0)
        mask2 = (tem < 0)
        tem_k=tem+273.15#换算成k
        e = 287.3/461.5*1000 #Rd/Rv g/kg
        es = np.zeros_like(tem_k)
        # 计算饱和水汽压
        es[mask1] = 6.1078 * np.exp( 17.2693882 * (tem_k[mask1]-273.16) / (tem_k[mask1]-35.86))
        es[mask2] = 6.112 * np.exp( 17.67 * (tem_k[mask2]-273.15) / (243.5 + tem_k[mask2]-273.15) )
        # 6.112 * np.exp( 17.67 * (tem_k[mask2]-273.15) / (243.5 + tem_k[mask2]-273.15) )
        # 6.1078 * np.exp(17.2693882 * (tem_k[mask2] - 273.16) / (tem_k[mask2] - 35.86))
        qs=np.zeros([len(tem_k),len(p)])#计算饱和比湿
        for i in range(len(tem_k)):
            for j in range(len(p)):
                qs[i,j]=(es[i]*e) / (p[j]-0.378*es[i])
        return np.round(qs,1)
    def theta_se_cal(self,tem, p, q):#计算假相当位温
        # 常量
        R = 287.3  # 气体常数 (J/(kg·K))  (8.314472/(28.9634*1e-3 )
        cp = 1004.8  # 比热容 (J/(kg·K))
        Lv = 2500.8  # 潜热 (J/kg) 假定气化潜热为常数，实际上随温度变化而变化
        p0 = 1000  # 基准压力 (hPa)
        tem_k = tem + 273.15  # 转换为开尔文
        theta_se = np.ones([len(tem), len(p)])#计算假相当位温
        for i in range(len(tem)):
            for j in range(len(p)):
                if q[i,j]<=1e-4:
                    theta_se[i, j] = tem_k[i] * (p0 / p[j]) ** (R/cp) * np.exp((Lv * 1e-3) / (cp * tem_k[i]))
                else:
                    theta_se[i, j] = tem_k[i] * (p0 / p[j]) ** (R/cp) * np.exp((Lv * q[i,j]) / (cp * tem_k[i]))
        return np.round(theta_se, 1)-273.15#返回摄氏度(方便绘图)

#示例数据
temperature = np.arange(-80, 221, 10)#温度范围
pressure=np.arange(200, 1001, 100)#压强范围
#更改0.5来改变精度，越小精度越高，但是计算成本高
temperature_like = np.arange(-90, 83, 0.1)
pressure_like=np.arange(200, 1050, 0.1)
#-----绘制T-lnP图----
t_lnp=T_lnp()
#根据示例数据计算相应的参量
theta= t_lnp.theta_cal(temperature_like,pressure_like)
qs= t_lnp.equal_saturation_q(temperature_like,pressure_like)
theta_se = t_lnp.theta_se_cal(temperature_like, pressure_like, qs)
# 绘制 T-lnp 图
fig=plt.figure(figsize=(10, 6))
ax=fig.add_subplot(111)
ax.set_xticks(temperature)
#设置xy轴界限
ax.set_xlim(-85,40)
ax.set_ylim(1050, 200)
ax.set_yscale('log')#y轴转对数
#绘制等位温，等饱和比湿，等假相当位温线
ax.contour(temperature_like,pressure_like,theta.T,levels=temperature,colors='brown', linewidths=1.5,linestyles='solid',alpha=0.7)
contour=ax.contour(temperature_like,pressure_like,qs.T,levels=[0.01,0.05,0.1,0.2,0.3,0.4,0.5,0.6,0.8,1.0,1.3,1.5,2.0,
                   2.5,3,4,5,6,8,10,12,14,16,18,20,25,30,35,40],colors='green',
                   linewidths=1.5,linestyles='solid',alpha=0.7)
contour_qs=ax.contour(temperature_like,pressure_like,theta_se.T,levels=np.arange(-40,181,10),colors='green',
                   linewidths=1.5,linestyles='dashed')
#标出值
ax.clabel(contour,inline=True,fmt="%2.2f")
ax.clabel(contour_qs,inline=True,fmt="%2.0f",fontsize=8,colors='k')
ax.set_yticks(pressure,[200,300,400,500,600,700,800,900,1000])
#绘图设置
ax.set_title('T-lnP')
ax.set_title('lnP [hPa]',loc='left')
plt.grid(True)
plt.show()

结果展示

结果如上。

图中，棕色实斜线为干绝热线，绿色斜实线为等饱和比湿线，绿色斜虚线为湿绝热线。

实际分析

以上只是简单绘制了T-lnP图，而没有将实际数据导入进行可视化分析与计算。

为了根据温度和相对湿度绘制T-lnP图，我们首先需要计算露点。

这里我使用ECMWF（European Centre for Medium-Range Weather Forecasts）的再分析资料ECMWF Reanalysis v5（ERA5）数据进行可视化。选择了各个高度层相对湿度（%）以及露点温温度(K)。

ERA5再分析资料的下载地址：ERA5 hourly data on pressure levels from 1940 to present (copernicus.eu)

计算露点

计算露点的方法在0℃以上参考了Tetens经验公式（Murray，1986），在0℃以下参考了Bolton指出的参考公式以及Arden Buck在Journal of Applied Meteorology and Climatology提出的经验公式。具体说明可看：

#https://en.wikipedia.org/wiki/Dew_point

代码如下：

class Dew_point():#https://en.wikipedia.org/wiki/Dew_point
    def Cal_dewpoint(self,T, RH):#计算露点函数
        # 第一区间参数 (0°C ≤ T ≤ 50°C)
        a1, b1, c1 = 6.1121, 17.368, 238.88
        # 第二区间参数 (−40°C ≤ T ≤ 0°C)
        a2, b2, c2 = 6.1121, 17.966, 247.15
        Td = xr.full_like(T, np.nan)  # 创建与 T 相同维度的空数组
        # 计算第一区间
        mask1 = (T >= 0) & (T <= 50)
        Td = Td.where(~mask1, (c1 * (np.log(RH / 100) + b1 * T / (c1 + T))) / \
                      (b1 - (np.log(RH / 100) + b1 * T / (c1 + T))))
        # 计算第二区间
        mask2 = (T >= -40) & (T < 0)
        Td = Td.where(~mask2, (c2 * (np.log(RH / 100) + b2 * T / (c2 + T))) / \
                      (b2 - (np.log(RH / 100) + b2 * T / (c2 + T))))
        # 计算第三区间
        b, c =17.62, 243.12 #T<=-40
        mask3 = (T < -40)
        Td=Td.where(~mask3,(c *( np.log(RH/100)+b*T/(c+T) ) )/(b- ( np.log(RH/100)+b*T/(c+T) )) )
        return Td
    def Cal_dewpoint1(self,T, RH):#第二种计算露点的公式
        b, c =17.62, 243.12 #-45<=T<=60
        Td=(c *( np.log(RH/100)+b*T/(c+T) ) )/(b- ( np.log(RH/100)+b*T/(c+T) ))
        return Td

大气的静力稳定度分析

为了分析实际大气的静力稳定度，在计算露点之后，还需要计算LCL，CCL，LFC，CAPE，CIN等参量，以下是计算代码，参考了以上各个公式。

class Stability:
    def __init__(self):
        self.LFC_Z,self.LFC_P=None,None
        self.D_Z,self.D_P = None,None
        self.LCL_Z,self.LCL_P=None,None
        self.LCL_theta_se=None
        self.LCL_Z,self.LCL_P=None,None
        self.tem_k_sel=None
    def LCL(self,T,Td):
        T_1000=T[0]#地面温度
        Td_1000 = Td[0]#地面露点
        LCL_Z=np.array(1000/(9.8-1.7)*(T_1000-Td_1000))#抬升凝结高度
        T_mean=(2*T_1000-(LCL_Z*9.8/1000))/2+273.15#干绝热下气层平均温度
        LCL_P=np.array(1000*np.exp(- (LCL_Z*9.80665) / (287.3*T_mean) ))
        self.LCL_Z, self.LCL_P=LCL_Z,LCL_P
        return LCL_Z,LCL_P
    def CCL(self,T,Td):
        T=T+273.15#气层温度换算为k
        Td_1000 = Td[0]+273.15#1000hpa露点温度
        e = 287.3 / 461.5 * 1000#Rd/Rv
        e_real=6.1078 * np.exp( 17.2693882 * (Td_1000-273.16) / (Td_1000-35.86))#实际水汽压
        q= np.array((e_real * e) / (1000 - 0.378 * e_real))#实际比湿
        es=6.1078 * np.exp( 17.2693882 * (T-273.16) / (T-35.86))#饱和水汽压
        qs= (es * e) / (1000 - 0.378 * es)#饱和比湿
        #---进行插值，寻找更精确的高度---
        new_pressure_levels = np.arange(1000, 0, -5)  # 从 1000 到 0 hPa，间隔为 5 hPa
        # 创建插值函数 对温度和比湿插值
        interp_function = interp1d(qs.pressure_level, qs, kind='linear', fill_value='extrapolate')
        interp_function_T=interp1d(qs.pressure_level, T, kind='linear', fill_value='extrapolate')
        # 计算新的比湿、温度数组
        qs_interp = interp_function(new_pressure_levels)
        T_interp = interp_function_T(new_pressure_levels)
        #寻找误差最小值点
        min_loc=np.min(np.abs(q - qs_interp))
        indice=np.where(np.abs(q - qs_interp)==min_loc)
        CCL_P=np.array(new_pressure_levels[indice])
        # 提取 T_interp 中在CCL_P之下的温度
        T_mean = np.mean(T_interp[new_pressure_levels < CCL_P[0]])
        CCL_Z=287.3*T_mean/9.80665*np.log(1000/CCL_P)
        #计算热对流下限温度TCON
        TCON=T_interp[indice]+CCL_Z/1000*9.8-273.15#换算回摄氏度
        return CCL_Z[0],CCL_P[0],TCON[0]
    def LFC(self,T,Td,level=None):#自由对流高度
        e = 287.3 / 461.5 * 1000  # Rd/Rv
        # 常量
        R = 287.3  # 气体常数 (J/(kg·K))  (8.314472/(28.9634*1e-3 )
        cp = 1004.8  # 比热容 (J/(kg·K))
        Lv = 2500.8  # 潜热 (J/kg)
        p0 = 1000  # 基准压力 (hPa)
        T_1000=T[0]+273.15#地面气层温度
        #---进行插值，寻找更精确的高度---
        new_pressure_levels = np.arange(1000, 200, -5)  # 从 1000 到 200 hPa，间隔为 5 hPa
        # 创建插值函数
        interp_function_T = interp1d(T.pressure_level, T, kind='linear', fill_value='extrapolate')
        interp_function_Td=interp1d(Td.pressure_level, Td, kind='linear', fill_value='extrapolate')
        # 计算新的比湿、温度数组
        indice_level=np.where(new_pressure_levels==level)#压强位置索引
        T_interp = interp_function_T(new_pressure_levels)+273.15#换算成k
        Td_interp = interp_function_Td(new_pressure_levels)+273.15#换算成k
        T_sel,Td_sel=T_interp[indice_level],Td_interp[indice_level]
        #LCL处的各个参数
        LCL_Z=np.array(1000/(9.8-1.7)*(T_sel-Td_sel))[0]
        T_mean = (2 * T_sel[0] - (LCL_Z * 9.8 / 1000)) / 2 # 干绝热下气层平均温度
        LCL_P=np.array(1000*np.exp(- (LCL_Z*9.80665) / (R*T_mean) ))#LCL处气压
        LCL_T=T_1000-9.8*LCL_Z/1000#LCL处温度(K)
        LCL_e=6.1078 * np.exp( 17.2693882 * (LCL_T-273.16) / (LCL_T-35.86))#LCL处饱和水汽压
        LCL_q = (LCL_e * e) / (1000 - 0.378 * LCL_e)#LCL处饱和比湿
        #tem_k[i] * (p0 / p[j]) ** (R/cp) * np.exp((Lv * q[i,j]) / (cp * tem_k[i]))
        LCL_theta_se = np.array( LCL_T *(p0 / LCL_P) ** (R/cp) * np.exp((Lv * LCL_q) / (cp * LCL_T)) )
        self.LCL_theta_se=LCL_theta_se#赋值并继承
        #计算大气气层的位温
        T_a=T_interp
        theta_a=T_a*(1000/new_pressure_levels)**0.286 #(R / cp)
        # 计算大气气层的假相当位温
        e_a=6.1078 * np.exp( 17.2693882 * (T_a-273.16) / (T_a-35.86))#气层饱和水汽压
        q_a = (e_a * e) / (1000 - 0.378 * e_a)#气层处饱和比湿
        theta_se_a = np.array(theta_a*np.exp((Lv * q_a) / (cp * T_a)))#气层假相当位温
        LFC_Z, LFC_P,D_P,D_Z=[],[],None,None
        #寻找假相当位温交点,如果未找到输出None
        for i in range(len(theta_se_a)-2):#利用阈值
            thetase,thetase_minu,thetase_plus=theta_se_a[i],theta_se_a[i-1],theta_se_a[i+1]
            thetase_minu1, thetase_plus1=theta_se_a[i-2],theta_se_a[i+2]
            if (thetase_minu-LCL_theta_se)>0 and (thetase_plus-LCL_theta_se)<0:
                if (thetase_minu1-LCL_theta_se)>0 and (thetase_plus1-LCL_theta_se)<0:
                    indice=i-2
                    LFC_val=np.array(new_pressure_levels[indice])
                    #找最低点
                    LFC_P.append(LFC_val)#LFC_P
                    # 提取 T_interp 中在LFC_P之下的温度
                    T_mean = np.mean(T_interp[new_pressure_levels < LFC_val])
                    LFC_Z.append(287.3 * T_mean / 9.80665 * np.log(1000 / np.array(new_pressure_levels[indice])))#LFC_Z
            if (thetase_minu-LCL_theta_se)<0 and (thetase_plus-LCL_theta_se)>0:
                if (thetase_minu1-LCL_theta_se)<0 and (thetase_plus1-LCL_theta_se)>0:
                    indice1=i+2
                    # 找最高点
                    D_P = new_pressure_levels[indice1]
                    # 提取 T_interp 中在LFC_P之下的温度
                    T_mean = np.mean(T_interp[new_pressure_levels < D_P])
                    D_Z = 287.3 * T_mean / 9.80665 * np.log(1000 / D_P)
        LFC_Z, LFC_P=np.array(LFC_Z),np.array(LFC_P)
        # 确保平衡高度 D_P 在自由对流高度 LFC_P 之下
        if D_P is not None and D_P < LFC_P[0]:  # 如果 D_P 不为 None 且在 LFC_P 之下
            self.D_Z, self.D_P = D_Z, D_P  # 返回最低点 D
        else:
            self.D_Z, self.D_P = None, None  # 否则设为 None
        if LFC_Z.size != 0:
            self.LFC_Z,self.LFC_P=LFC_Z[0],LFC_P[0]#返回最低点LFC
        else:
            self.LFC_Z, self.LFC_P=None,None#未找到则返回None值
        self.LCL_Z,self.LCL_P=LCL_Z,LCL_P
        return self.LFC_Z,self.LFC_P,self.D_Z,self.D_P
    def CAPE(self,T):#对流有效势能
        # 常量
        R = 287.3  # 气体常数 (J/(kg·K))  (8.314472/(28.9634*1e-3 )
        cp = 1004.8  # 比热容 (J/(kg·K))
        Lv = 2500.8  # 潜热 (J/kg)
        p0 = 1000  # 基准压力 (hPa)
        e = 287.3/461.5*1000 #Rd/Rv
        if self.LFC_P!=None:#找到了自由对流高度
            if self.D_P==None:
                p = np.arange(self.LFC_P, 200, -0.1)  # 压高范围
            else:#如果找到平衡高度
                p = np.arange(self.LFC_P, self.D_P, -0.1)  # 压高范围
            tem=np.arange(-80, 61, 0.1)
            tem_k=tem+273.15
            mask1 = (tem >= 0)
            mask2 = (tem < 0)
            es = np.zeros_like(tem_k)
            # 计算饱和水汽压
            es[mask1] = 6.1078 * np.exp( 17.2693882 * (tem_k[mask1]-273.16) / (tem_k[mask1]-35.86))
            es[mask2] = 6.112 * np.exp( 17.67 * (tem_k[mask2]-273.15) / (243.5 + tem_k[mask2]-273.15) )
            #计算饱和比湿
            qs=np.zeros([len(tem_k),len(p)])
            for i in range(len(tem_k)):
                for j in range(len(p)):
                    qs[i,j]=(es[i]*e) / (p[j]-0.378*es[i])
            #计算假相当位温
            theta_se = np.ones([len(tem_k), len(p)])
            for i in range(len(tem_k)):
                for j in range(len(p)):
                        theta_se[i, j] = tem_k[i] * (p0 / p[j]) ** (R/cp) * np.exp((Lv * qs[i,j]) / (cp * tem_k[i]))
            # 查找与 self.LCL_theta_se 相等的 theta_se 值
            LCL_theta_se_value = self.LCL_theta_se
            indices = np.where((np.abs(theta_se - LCL_theta_se_value)<1e-4))  # 使用近似查找
            # 提取对应的 tem_k
            tem_k_sel = tem_k[indices[0]]  # 根据行索引提取对应的 tem_k
            tem_k_sel=np.flip(tem_k_sel)
            self.tem_k_sel=tem_k_sel#继承LCL假相当位温对应的温度
            new_pressure_levels = p
            # 线性插值
            interp_function_T = interp1d(T.pressure_level, T, kind='linear', fill_value='extrapolate')
            T_interp = interp_function_T(new_pressure_levels)+273.15#换算成k
            original_indices = np.arange(len(tem_k_sel))  # 原始索引
            new_indices = np.linspace(0, len(tem_k_sel) - 1, len(T_interp))  # 新的均匀索引
            # 使用 np.interp 进行线性插值
            tem_k_interp = np.interp(new_indices, original_indices, tem_k_sel)
            # 计算 tem_k_interp - T_interp
            difference = tem_k_interp - T_interp
            # 提取满足条件的温度和压力位置
            mask = difference > 0  # 只保留大于 0 的位置
            filtered_tem_k_interp = tem_k_interp[mask]
            filtered_p = p[mask]
            # 如果有大于0的位置
            if len(filtered_tem_k_interp) > 0 and len(filtered_p) > 0:
                # 计算 CAPE 只在 tem_k_interp - T_interp 大于 0 的地方
                cape_area = -simps(filtered_tem_k_interp - T_interp[mask], filtered_p)
            else:#否则返回0
                cape_area = 0
        else:
            cape_area=0
        return cape_area
    def CIN(self,T):#对流抑制能量
        T_1000=T[0]+ 273.15#换算K
        if self.LFC_P!=None:
            if self.LFC_P<self.LCL_P:#干湿绝热混合
                p1 = np.arange(self.LCL_P,self.LFC_P,-0.1)# 压高范围1
                p2 = np.arange(1000,self.LCL_P, -0.1)  # 压高范围2
                new_pressure_levels = p1
                tem_k_sel=self.tem_k_sel#继承等假相当位温线对应的温度
                # 线性插值
                interp_function_T = interp1d(T.pressure_level, T, kind='linear', fill_value='extrapolate')
                T_interp = interp_function_T(new_pressure_levels) + 273.15  # 换算成k
                original_indices = np.arange(len(tem_k_sel))  # 原始索引
                new_indices = np.linspace(0, len(tem_k_sel) - 1, len(T_interp))  # 新的均匀索引
                # 使用 np.interp 进行线性插值
                tem_k_interp = np.interp(new_indices, original_indices, tem_k_sel)
                # 计算 tem_k_interp - T_interp
                difference = tem_k_interp - T_interp
                # 提取满足条件的温度和压力位置
                mask = difference > 0  # 只保留大于 0 的位置
                filtered_tem_k_interp = tem_k_interp[mask]
                filtered_p = p1[mask]
                # 如果有大于0的位置
                if len(filtered_tem_k_interp) > 0 and len(filtered_p) > 0:
                    # 计算 CAPE 只在 tem_k_interp - T_interp 大于 0 的地方
                    cin_area = simps(filtered_tem_k_interp - T_interp[mask], filtered_p)
                else:
                    cin_area = 0  # 或者其他适当的默认值
                T_interp_d = interp_function_T(p2) + 273.15
                T_cin_d=np.linspace(T_1000,(T_1000-9.8*self.LCL_Z/1000),len(T_interp_d))
                cin_area_d=simps(T_cin_d - T_interp_d , p2)
                cin_area+=cin_area_d
            else:#干绝热(LFC在LCL下)
                p1 = np.arange(1000,self.LCL_P -0.1)  # 压高范围2
                new_pressure_levels = p1
                # 线性插值
                interp_function_T = interp1d(T.pressure_level, T, kind='linear', fill_value='extrapolate')
                T_interp = interp_function_T(new_pressure_levels) + 273.15  # 换算成k
                # 使用 np.interp 进行线性插值
                T_cin_d=np.linspace(T_1000,(T_1000-9.8*self.LCL_Z/1000),len(T_interp))
                cin_area=simps(T_cin_d - T_interp , p1)
        else:
            cin_area=0
        return cin_area

导入实际的nc数据，选择一个格点或者一片区域的平均温度和相对湿度进行尝试，这里以133.8°E，22.6°N的格点为例子，可视化了2024年10月1日UTC12时（北京时间晚上八点）的数据。

代码如下：

#----导入nc文件----
ds=xr.open_dataset(r"D:\ERA5\T-RH-2024.10.01-00-12.nc")
sel_time='2024-10-01T12:00:00.000000000'#数据时间段
rh,tem=ds.r,ds.t
#(valid_time: 24, pressure_level: 37, latitude: 721,longitude: 1440)
tem-=273.15#换算成摄氏度
rh=rh.where(rh>=0,1e-5)#处理相对湿度中的异常数据
Td_calculator=Dew_point()
#计算露点
td=Td_calculator.Cal_dewpoint(tem,rh)
location=[133.8,22.6]#选择经纬度
tem_loc=tem.sel(valid_time=sel_time,longitude=location[0],latitude=location[1],method='nearest')
td_loc=td.sel(valid_time=sel_time,longitude=location[0],latitude=location[1],method='nearest')
#----大气稳定度参数计算----
Stab_calculator=Stability()
LCL_z,LCL_p=Stab_calculator.LCL(tem_loc,td_loc)
CCL_z,CCL_p,TCON=Stab_calculator.CCL(tem_loc,td_loc)
level_sel=1000#气块初始高度
LFC_z,LFC_p,D_z,D_p=Stab_calculator.LFC(tem_loc,td_loc,level=level_sel)
cape_val=Stab_calculator.CAPE(tem_loc)
cin_val=Stab_calculator.CIN(tem_loc)
#数据分析

print('-------------数据分析-------------')
print(f'抬升凝结高度：{np.round(LCL_z,1)}m {np.round(LCL_p,1)}hpa')
print(f'对流凝结高度：{np.round(CCL_z,1)}m {np.round(CCL_p,1)}hpa')

if LFC_z!=None:
    if D_z!=None:
        print(f'{level_sel}hpa 自由对流高度：{np.round(LFC_z,1)}m {np.round(LFC_p,2)}hpa')
        print(f'{level_sel}hpa 平衡高度：{np.round(D_z,1)}m {np.round(D_p,1)}hpa')
    else:
        print(f'{level_sel}hpa 自由对流高度：{np.round(LFC_z, 1)}m {np.round(LFC_p, 2)}hpa')
        print('未找到平衡高度 !')
else:
    print('未找到自由对流高度 !')
    print('未找到平衡高度 !')
if LCL_z<CCL_z:
    print(f'气块凝结高度(对流云底高度): {np.round(CCL_z,1)}m')
else:
    print(f'气块凝结高度(对流云底高度): {np.round(LCL_z,1)}m')
print(f'热对流下限温度：{np.round(TCON,1)} C')
print(f'CAPE值(对流有效势能)：{np.round(cape_val,1)} J/Kg')
print(f'CIN值(对流抑制能量)：{np.round(cin_val,1)} J/Kg')
print('---------------结束---------------')

可视化结果与分析结果如下:

可以看到各个大气稳定度相关高度的计算结果与实际经纬度点上的温度与露点温度分布情况。

全部代码

import numpy as np
import matplotlib.pyplot as plt
import xarray as xr
from scipy.interpolate import interp1d
from scipy.integrate import simps
class Dew_point():#https://en.wikipedia.org/wiki/Dew_point
    def Cal_dewpoint(self,T, RH):#计算露点函数
        # 第一区间参数 (0°C ≤ T ≤ 50°C)
        a1, b1, c1 = 6.1121, 17.368, 238.88
        # 第二区间参数 (−40°C ≤ T ≤ 0°C)
        a2, b2, c2 = 6.1121, 17.966, 247.15
        Td = xr.full_like(T, np.nan)  # 创建与 T 相同维度的空数组
        # 计算第一区间
        mask1 = (T >= 0) & (T <= 50)
        Td = Td.where(~mask1, (c1 * (np.log(RH / 100) + b1 * T / (c1 + T))) / \
                      (b1 - (np.log(RH / 100) + b1 * T / (c1 + T))))
        # 计算第二区间
        mask2 = (T >= -40) & (T < 0)
        Td = Td.where(~mask2, (c2 * (np.log(RH / 100) + b2 * T / (c2 + T))) / \
                      (b2 - (np.log(RH / 100) + b2 * T / (c2 + T))))
        # 计算第三区间
        b, c =17.62, 243.12 #T<=-40
        mask3 = (T < -40)
        Td=Td.where(~mask3,(c *( np.log(RH/100)+b*T/(c+T) ) )/(b- ( np.log(RH/100)+b*T/(c+T) )) )
        return Td
    def Cal_dewpoint1(self,T, RH):#第二种计算露点的公式
        b, c =17.62, 243.12 #-45<=T<=60
        Td=(c *( np.log(RH/100)+b*T/(c+T) ) )/(b- ( np.log(RH/100)+b*T/(c+T) ))
        return Td
class T_lnp():
    def theta_cal(self,tem,p):#计算位温
        tem=tem+273.15#换算成k
        theta=np.ones([len(tem),len(p)])
        for i in range(len(tem)):
            for j in range(len(p)):
                theta[i,j]=tem[i]*(1000/p[j])**0.286 #(R / cp)
        theta=theta-273.15#换算为摄氏度
        return np.round(theta,1)
    def equal_saturation_q(self,tem, p):#计算等饱和比湿
        mask1 = (tem >= 0)
        mask2 = (tem < 0)
        tem_k=tem+273.15#换算成k
        e = 287.3/461.5*1000 #Rd/Rv g/kg
        es = np.zeros_like(tem_k)
        # 计算饱和水汽压
        es[mask1] = 6.1078 * np.exp( 17.2693882 * (tem_k[mask1]-273.16) / (tem_k[mask1]-35.86))
        es[mask2] = 6.112 * np.exp( 17.67 * (tem_k[mask2]-273.15) / (243.5 + tem_k[mask2]-273.15) )
        # 6.112 * np.exp( 17.67 * (tem_k[mask2]-273.15) / (243.5 + tem_k[mask2]-273.15) )
        # 6.1078 * np.exp(17.2693882 * (tem_k[mask2] - 273.16) / (tem_k[mask2] - 35.86))
        qs=np.zeros([len(tem_k),len(p)])#计算饱和比湿
        for i in range(len(tem_k)):
            for j in range(len(p)):
                qs[i,j]=(es[i]*e) / (p[j]-0.378*es[i])
        return np.round(qs,1)
    def theta_se_cal(self,tem, p, q):#计算假相当位温
        # 常量
        R = 287.3  # 气体常数 (J/(kg·K))  (8.314472/(28.9634*1e-3 )
        cp = 1004.8  # 比热容 (J/(kg·K))
        Lv = 2500.8  # 潜热 (J/kg) 假定气化潜热为常数，实际上随温度变化而变化
        p0 = 1000  # 基准压力 (hPa)
        tem_k = tem + 273.15  # 转换为开尔文
        theta_se = np.ones([len(tem), len(p)])#计算假相当位温
        for i in range(len(tem)):
            for j in range(len(p)):
                if q[i,j]<=1e-4:
                    theta_se[i, j] = tem_k[i] * (p0 / p[j]) ** (R/cp) * np.exp((Lv * 1e-3) / (cp * tem_k[i]))
                else:
                    theta_se[i, j] = tem_k[i] * (p0 / p[j]) ** (R/cp) * np.exp((Lv * q[i,j]) / (cp * tem_k[i]))
        return np.round(theta_se, 1)-273.15#返回摄氏度(方便绘图)
class Stability:
    def __init__(self):
        self.LFC_Z,self.LFC_P=None,None
        self.D_Z,self.D_P = None,None
        self.LCL_Z,self.LCL_P=None,None
        self.LCL_theta_se=None
        self.LCL_Z,self.LCL_P=None,None
        self.tem_k_sel=None
    def LCL(self,T,Td):
        T_1000=T[0]#地面温度
        Td_1000 = Td[0]#地面露点
        LCL_Z=np.array(1000/(9.8-1.7)*(T_1000-Td_1000))#抬升凝结高度
        T_mean=(2*T_1000-(LCL_Z*9.8/1000))/2+273.15#干绝热下气层平均温度
        LCL_P=np.array(1000*np.exp(- (LCL_Z*9.80665) / (287.3*T_mean) ))
        self.LCL_Z, self.LCL_P=LCL_Z,LCL_P
        return LCL_Z,LCL_P
    def CCL(self,T,Td):
        T=T+273.15#气层温度换算为k
        Td_1000 = Td[0]+273.15#1000hpa露点温度
        e = 287.3 / 461.5 * 1000#Rd/Rv
        e_real=6.1078 * np.exp( 17.2693882 * (Td_1000-273.16) / (Td_1000-35.86))#实际水汽压
        q= np.array((e_real * e) / (1000 - 0.378 * e_real))#实际比湿
        es=6.1078 * np.exp( 17.2693882 * (T-273.16) / (T-35.86))#饱和水汽压
        qs= (es * e) / (1000 - 0.378 * es)#饱和比湿
        #---进行插值，寻找更精确的高度---
        new_pressure_levels = np.arange(1000, 0, -5)  # 从 1000 到 0 hPa，间隔为 5 hPa
        # 创建插值函数 对温度和比湿插值
        interp_function = interp1d(qs.pressure_level, qs, kind='linear', fill_value='extrapolate')
        interp_function_T=interp1d(qs.pressure_level, T, kind='linear', fill_value='extrapolate')
        # 计算新的比湿、温度数组
        qs_interp = interp_function(new_pressure_levels)
        T_interp = interp_function_T(new_pressure_levels)
        #寻找误差最小值点
        min_loc=np.min(np.abs(q - qs_interp))
        indice=np.where(np.abs(q - qs_interp)==min_loc)
        CCL_P=np.array(new_pressure_levels[indice])
        # 提取 T_interp 中在CCL_P之下的温度
        T_mean = np.mean(T_interp[new_pressure_levels < CCL_P[0]])
        CCL_Z=287.3*T_mean/9.80665*np.log(1000/CCL_P)
        #计算热对流下限温度TCON
        TCON=T_interp[indice]+CCL_Z/1000*9.8-273.15#换算回摄氏度
        return CCL_Z[0],CCL_P[0],TCON[0]
    def LFC(self,T,Td,level=None):#自由对流高度
        e = 287.3 / 461.5 * 1000  # Rd/Rv
        # 常量
        R = 287.3  # 气体常数 (J/(kg·K))  (8.314472/(28.9634*1e-3 )
        cp = 1004.8  # 比热容 (J/(kg·K))
        Lv = 2500.8  # 潜热 (J/kg)
        p0 = 1000  # 基准压力 (hPa)
        T_1000=T[0]+273.15#地面气层温度
        #---进行插值，寻找更精确的高度---
        new_pressure_levels = np.arange(1000, 200, -5)  # 从 1000 到 200 hPa，间隔为 5 hPa
        # 创建插值函数
        interp_function_T = interp1d(T.pressure_level, T, kind='linear', fill_value='extrapolate')
        interp_function_Td=interp1d(Td.pressure_level, Td, kind='linear', fill_value='extrapolate')
        # 计算新的比湿、温度数组
        indice_level=np.where(new_pressure_levels==level)#压强位置索引
        T_interp = interp_function_T(new_pressure_levels)+273.15#换算成k
        Td_interp = interp_function_Td(new_pressure_levels)+273.15#换算成k
        T_sel,Td_sel=T_interp[indice_level],Td_interp[indice_level]
        #LCL处的各个参数
        LCL_Z=np.array(1000/(9.8-1.7)*(T_sel-Td_sel))[0]
        T_mean = (2 * T_sel[0] - (LCL_Z * 9.8 / 1000)) / 2 # 干绝热下气层平均温度
        LCL_P=np.array(1000*np.exp(- (LCL_Z*9.80665) / (R*T_mean) ))#LCL处气压
        LCL_T=T_1000-9.8*LCL_Z/1000#LCL处温度(K)
        LCL_e=6.1078 * np.exp( 17.2693882 * (LCL_T-273.16) / (LCL_T-35.86))#LCL处饱和水汽压
        LCL_q = (LCL_e * e) / (1000 - 0.378 * LCL_e)#LCL处饱和比湿
        #tem_k[i] * (p0 / p[j]) ** (R/cp) * np.exp((Lv * q[i,j]) / (cp * tem_k[i]))
        LCL_theta_se = np.array( LCL_T *(p0 / LCL_P) ** (R/cp) * np.exp((Lv * LCL_q) / (cp * LCL_T)) )
        self.LCL_theta_se=LCL_theta_se#赋值并继承
        #计算大气气层的位温
        T_a=T_interp
        theta_a=T_a*(1000/new_pressure_levels)**0.286 #(R / cp)
        # 计算大气气层的假相当位温
        e_a=6.1078 * np.exp( 17.2693882 * (T_a-273.16) / (T_a-35.86))#气层饱和水汽压
        q_a = (e_a * e) / (1000 - 0.378 * e_a)#气层处饱和比湿
        theta_se_a = np.array(theta_a*np.exp((Lv * q_a) / (cp * T_a)))#气层假相当位温
        LFC_Z, LFC_P,D_P,D_Z=[],[],None,None
        #寻找假相当位温交点,如果未找到输出None
        for i in range(len(theta_se_a)-2):#利用阈值
            thetase,thetase_minu,thetase_plus=theta_se_a[i],theta_se_a[i-1],theta_se_a[i+1]
            thetase_minu1, thetase_plus1=theta_se_a[i-2],theta_se_a[i+2]
            if (thetase_minu-LCL_theta_se)>0 and (thetase_plus-LCL_theta_se)<0:
                if (thetase_minu1-LCL_theta_se)>0 and (thetase_plus1-LCL_theta_se)<0:
                    indice=i-2
                    LFC_val=np.array(new_pressure_levels[indice])
                    #找最低点
                    LFC_P.append(LFC_val)#LFC_P
                    # 提取 T_interp 中在LFC_P之下的温度
                    T_mean = np.mean(T_interp[new_pressure_levels < LFC_val])
                    LFC_Z.append(287.3 * T_mean / 9.80665 * np.log(1000 / np.array(new_pressure_levels[indice])))#LFC_Z
            if (thetase_minu-LCL_theta_se)<0 and (thetase_plus-LCL_theta_se)>0:
                if (thetase_minu1-LCL_theta_se)<0 and (thetase_plus1-LCL_theta_se)>0:
                    indice1=i+2
                    # 找最高点
                    D_P = new_pressure_levels[indice1]
                    # 提取 T_interp 中在LFC_P之下的温度
                    T_mean = np.mean(T_interp[new_pressure_levels < D_P])
                    D_Z = 287.3 * T_mean / 9.80665 * np.log(1000 / D_P)
        LFC_Z, LFC_P=np.array(LFC_Z),np.array(LFC_P)
        # 确保平衡高度 D_P 在自由对流高度 LFC_P 之下
        if D_P is not None and D_P < LFC_P[0]:  # 如果 D_P 不为 None 且在 LFC_P 之下
            self.D_Z, self.D_P = D_Z, D_P  # 返回最低点 D
        else:
            self.D_Z, self.D_P = None, None  # 否则设为 None
        if LFC_Z.size != 0:
            self.LFC_Z,self.LFC_P=LFC_Z[0],LFC_P[0]#返回最低点LFC
        else:
            self.LFC_Z, self.LFC_P=None,None#未找到则返回None值
        self.LCL_Z,self.LCL_P=LCL_Z,LCL_P
        return self.LFC_Z,self.LFC_P,self.D_Z,self.D_P
    def CAPE(self,T):#对流有效势能
        # 常量
        R = 287.3  # 气体常数 (J/(kg·K))  (8.314472/(28.9634*1e-3 )
        cp = 1004.8  # 比热容 (J/(kg·K))
        Lv = 2500.8  # 潜热 (J/kg)
        p0 = 1000  # 基准压力 (hPa)
        e = 287.3/461.5*1000 #Rd/Rv
        if self.LFC_P!=None:#找到了自由对流高度
            if self.D_P==None:
                p = np.arange(self.LFC_P, 200, -0.1)  # 压高范围
            else:#如果找到平衡高度
                p = np.arange(self.LFC_P, self.D_P, -0.1)  # 压高范围
            tem=np.arange(-80, 61, 0.1)
            tem_k=tem+273.15
            mask1 = (tem >= 0)
            mask2 = (tem < 0)
            es = np.zeros_like(tem_k)
            # 计算饱和水汽压
            es[mask1] = 6.1078 * np.exp( 17.2693882 * (tem_k[mask1]-273.16) / (tem_k[mask1]-35.86))
            es[mask2] = 6.112 * np.exp( 17.67 * (tem_k[mask2]-273.15) / (243.5 + tem_k[mask2]-273.15) )
            #计算饱和比湿
            qs=np.zeros([len(tem_k),len(p)])
            for i in range(len(tem_k)):
                for j in range(len(p)):
                    qs[i,j]=(es[i]*e) / (p[j]-0.378*es[i])
            #计算假相当位温
            theta_se = np.ones([len(tem_k), len(p)])
            for i in range(len(tem_k)):
                for j in range(len(p)):
                        theta_se[i, j] = tem_k[i] * (p0 / p[j]) ** (R/cp) * np.exp((Lv * qs[i,j]) / (cp * tem_k[i]))
            # 查找与 self.LCL_theta_se 相等的 theta_se 值
            LCL_theta_se_value = self.LCL_theta_se
            indices = np.where((np.abs(theta_se - LCL_theta_se_value)<1e-4))  # 使用近似查找
            # 提取对应的 tem_k
            tem_k_sel = tem_k[indices[0]]  # 根据行索引提取对应的 tem_k
            tem_k_sel=np.flip(tem_k_sel)
            self.tem_k_sel=tem_k_sel#继承LCL假相当位温对应的温度
            new_pressure_levels = p
            # 线性插值
            interp_function_T = interp1d(T.pressure_level, T, kind='linear', fill_value='extrapolate')
            T_interp = interp_function_T(new_pressure_levels)+273.15#换算成k
            original_indices = np.arange(len(tem_k_sel))  # 原始索引
            new_indices = np.linspace(0, len(tem_k_sel) - 1, len(T_interp))  # 新的均匀索引
            # 使用 np.interp 进行线性插值
            tem_k_interp = np.interp(new_indices, original_indices, tem_k_sel)
            # 计算 tem_k_interp - T_interp
            difference = tem_k_interp - T_interp
            # 提取满足条件的温度和压力位置
            mask = difference > 0  # 只保留大于 0 的位置
            filtered_tem_k_interp = tem_k_interp[mask]
            filtered_p = p[mask]
            # 如果有大于0的位置
            if len(filtered_tem_k_interp) > 0 and len(filtered_p) > 0:
                # 计算 CAPE 只在 tem_k_interp - T_interp 大于 0 的地方
                cape_area = -simps(filtered_tem_k_interp - T_interp[mask], filtered_p)
            else:#否则返回0
                cape_area = 0
        else:
            cape_area=0
        return cape_area
    def CIN(self,T):#对流抑制能量
        T_1000=T[0]+ 273.15#换算K
        if self.LFC_P!=None:
            if self.LFC_P<self.LCL_P:#干湿绝热混合
                p1 = np.arange(self.LCL_P,self.LFC_P,-0.1)# 压高范围1
                p2 = np.arange(1000,self.LCL_P, -0.1)  # 压高范围2
                new_pressure_levels = p1
                tem_k_sel=self.tem_k_sel#继承等假相当位温线对应的温度
                # 线性插值
                interp_function_T = interp1d(T.pressure_level, T, kind='linear', fill_value='extrapolate')
                T_interp = interp_function_T(new_pressure_levels) + 273.15  # 换算成k
                original_indices = np.arange(len(tem_k_sel))  # 原始索引
                new_indices = np.linspace(0, len(tem_k_sel) - 1, len(T_interp))  # 新的均匀索引
                # 使用 np.interp 进行线性插值
                tem_k_interp = np.interp(new_indices, original_indices, tem_k_sel)
                # 计算 tem_k_interp - T_interp
                difference = tem_k_interp - T_interp
                # 提取满足条件的温度和压力位置
                mask = difference > 0  # 只保留大于 0 的位置
                filtered_tem_k_interp = tem_k_interp[mask]
                filtered_p = p1[mask]
                # 如果有大于0的位置
                if len(filtered_tem_k_interp) > 0 and len(filtered_p) > 0:
                    # 计算 CAPE 只在 tem_k_interp - T_interp 大于 0 的地方
                    cin_area = simps(filtered_tem_k_interp - T_interp[mask], filtered_p)
                else:
                    cin_area = 0  # 或者其他适当的默认值
                T_interp_d = interp_function_T(p2) + 273.15
                T_cin_d=np.linspace(T_1000,(T_1000-9.8*self.LCL_Z/1000),len(T_interp_d))
                cin_area_d=simps(T_cin_d - T_interp_d , p2)
                cin_area+=cin_area_d
            else:#干绝热(LFC在LCL下)
                p1 = np.arange(1000,self.LCL_P -0.1)  # 压高范围2
                new_pressure_levels = p1
                # 线性插值
                interp_function_T = interp1d(T.pressure_level, T, kind='linear', fill_value='extrapolate')
                T_interp = interp_function_T(new_pressure_levels) + 273.15  # 换算成k
                # 使用 np.interp 进行线性插值
                T_cin_d=np.linspace(T_1000,(T_1000-9.8*self.LCL_Z/1000),len(T_interp))
                cin_area=simps(T_cin_d - T_interp , p1)
        else:
            cin_area=0
        return cin_area
#示例数据
temperature = np.arange(-80, 221, 10)#温度范围
pressure=np.arange(200, 1001, 100)#压强范围
#更改0.5来改变精度，越小精度越高，但是计算成本高
temperature_like = np.arange(-90, 83, 0.5)
pressure_like=np.arange(200, 1050, 0.5)
#-----绘制T-lnP图----
t_lnp=T_lnp()
#根据示例数据计算相应的参量
theta= t_lnp.theta_cal(temperature_like,pressure_like)
qs= t_lnp.equal_saturation_q(temperature_like,pressure_like)
theta_se = t_lnp.theta_se_cal(temperature_like, pressure_like, qs)

#----导入nc文件----
ds=xr.open_dataset(r"D:\ERA5\T-RH-2024.10.01-00-12.nc")
sel_time='2024-10-01T12:00:00.000000000'#数据时间段
rh,tem=ds.r,ds.t
#(valid_time: 24, pressure_level: 37, latitude: 721,longitude: 1440)
tem-=273.15#换算成摄氏度
rh=rh.where(rh>=0,1e-5)#处理相对湿度中的异常数据
Td_calculator=Dew_point()
#计算露点
td=Td_calculator.Cal_dewpoint(tem,rh)
location=[133.8,22.6]#选择经纬度
tem_loc=tem.sel(valid_time=sel_time,longitude=location[0],latitude=location[1],method='nearest')
td_loc=td.sel(valid_time=sel_time,longitude=location[0],latitude=location[1],method='nearest')
#----大气稳定度参数计算----
Stab_calculator=Stability()
LCL_z,LCL_p=Stab_calculator.LCL(tem_loc,td_loc)
CCL_z,CCL_p,TCON=Stab_calculator.CCL(tem_loc,td_loc)
level_sel=1000#气块初始高度
LFC_z,LFC_p,D_z,D_p=Stab_calculator.LFC(tem_loc,td_loc,level=level_sel)
cape_val=Stab_calculator.CAPE(tem_loc)
cin_val=Stab_calculator.CIN(tem_loc)
#数据分析

print('-------------数据分析-------------')
print(f'抬升凝结高度：{np.round(LCL_z,1)}m {np.round(LCL_p,1)}hpa')
print(f'对流凝结高度：{np.round(CCL_z,1)}m {np.round(CCL_p,1)}hpa')

if LFC_z!=None:
    if D_z!=None:
        print(f'{level_sel}hpa 自由对流高度：{np.round(LFC_z,1)}m {np.round(LFC_p,2)}hpa')
        print(f'{level_sel}hpa 平衡高度：{np.round(D_z,1)}m {np.round(D_p,1)}hpa')
    else:
        print(f'{level_sel}hpa 自由对流高度：{np.round(LFC_z, 1)}m {np.round(LFC_p, 2)}hpa')
        print('未找到平衡高度 !')
else:
    print('未找到自由对流高度 !')
    print('未找到平衡高度 !')
if LCL_z<CCL_z:
    print(f'气块凝结高度(对流云底高度): {np.round(CCL_z,1)}m')
else:
    print(f'气块凝结高度(对流云底高度): {np.round(LCL_z,1)}m')
print(f'热对流下限温度：{np.round(TCON,1)} C')
print(f'CAPE值(对流有效势能)：{np.round(cape_val,1)} J/Kg')
print(f'CIN值(对流抑制能量)：{np.round(cin_val,1)} J/Kg')
print('---------------结束---------------')

# 绘制 T-lnp 图
fig=plt.figure(figsize=(10, 6))
ax=fig.add_subplot(111)
ax.set_xticks(temperature)
#设置xy轴界限
ax.set_xlim(-85,40)
ax.set_ylim(1050, 200)
ax.set_yscale('log')#y轴转对数
#绘制等位温，等饱和比湿，等假相当位温线
ax.contour(temperature_like,pressure_like,theta.T,levels=temperature,colors='brown', linewidths=1.5,linestyles='solid',alpha=0.7)
contour=ax.contour(temperature_like,pressure_like,qs.T,levels=[0.01,0.05,0.1,0.2,0.3,0.4,0.5,0.6,0.8,1.0,1.3,1.5,2.0,
                   2.5,3,4,5,6,8,10,12,14,16,18,20,25,30,35,40],colors='green',
                   linewidths=1.5,linestyles='solid',alpha=0.7)
contour_qs=ax.contour(temperature_like,pressure_like,theta_se.T,levels=np.arange(-40,181,10),colors='green',
                   linewidths=1.5,linestyles='dashed')
#标出值
ax.clabel(contour,inline=True,fmt="%2.2f")
ax.clabel(contour_qs,inline=True,fmt="%2.0f",fontsize=8,colors='k')
#绘制气层的露点与温度
ax.plot(tem_loc,tem_loc.pressure_level,c='red')
ax.plot(td_loc,td_loc.pressure_level,c='blue')
ax.set_yticks(pressure,[200,300,400,500,600,700,800,900,1000])
#绘图设置
ax.set_title('T-lnP')
ax.set_title('lnP [hPa]',loc='left')
ax.set_title(f'{location[0]}$^o$ {location[1]}$^o$',loc='right',
             font='Times New Roman',fontsize=8,fontweight='bold')
ax.set_xlabel(f'Tem [°C]\n '
              f'CIN:{np.round(cin_val,1)} J/Kg    '
              f'CAPE:{np.round(cape_val,1)} J/Kg    '
              f'  LFC:{np.round(LFC_z,1)} m    '
              f'  TCON:{np.round(TCON,1)} $^o$C     '
              f'  CCL:{np.round(CCL_z,1)} m    '
              f'  LCL:{np.round(LCL_z,1)} m',loc='right')
plt.grid(True)
plt.show()

CAPE值和CIN值可能会存在一定的差异，而且计算时间成本较高，后续会考虑其他方式进行计算，这里只是用传统T-lnP图的计算方法来进行计算，更贴合T-lnP图内容。